Previous Page
   Next Page
 
Evokation
  
 
Index
  

 

 

 

 

A

MAZE

IN

ZAZAZA ENTERS AZAZAZ

AZAZAZAZAZAZAZZAZAZAZAZAZAZA

ZAZAZAZAZAZAZAZAZAAZAZAZAZAZAZAZAZAZ

THE

MAGICALALPHABET

ABCDEFGHIJKLMNOPQRSTUVWXYZZYXWVUTSRQPONMLKJIHGFEDCBA

12345678910111213141516171819202122232425262625242322212019181716151413121110987654321

 

 

26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
8
9
-
-
-
-
5
6
-
-
-
1
-
-
-
-
6
-
8
+
=
43
4+3
=
7
-
7
-
7
-
-
-
-
-
-
-
-
8
9
-
-
-
-
14
15
-
-
-
19
-
-
-
-
24
-
26
+
=
115
1+1+5
=
7
-
7
-
7
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
-
-
1
2
3
4
-
-
7
8
9
-
2
3
4
5
-
7
-
+
=
83
8+3
=
11
1+1
2
-
2
-
1
2
3
4
5
6
7
-
-
10
11
12
13
-
-
16
17
18
-
20
21
22
23
-
25
-
+
=
236
2+3+6
=
11
1+1
2
-
2
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
+
=
351
3+5+1
=
9
-
9
-
9
-
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
+
=
126
1+2+6
=
9
-
9
-
9
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
+
=
1
occurs
x
3
=
3
-
3
-
-
2
-
-
-
-
-
-
-
-
2
-
-
-
-
-
-
-
-
2
-
-
-
-
-
-
+
=
2
occurs
x
3
=
6
-
6
-
-
-
3
-
-
-
-
-
-
-
-
3
-
-
-
-
-
-
-
-
3
-
-
-
-
-
+
=
3
occurs
x
3
=
9
-
9
-
-
-
-
4
-
-
-
-
-
-
-
-
4
-
-
-
-
-
-
-
-
4
-
-
-
-
+
=
4
occurs
x
3
=
12
1+2
3
-
-
-
-
-
5
-
-
-
-
-
-
-
-
5
-
-
-
-
-
-
-
-
5
-
-
-
+
=
5
occurs
x
3
=
15
1+5
6
-
-
-
-
-
-
6
-
-
-
-
-
-
-
-
6
-
-
-
-
-
-
-
-
6
-
-
+
=
6
occurs
x
3
=
18
1+8
9
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
-
7
-
+
=
7
occurs
x
3
=
21
2+1
3
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
8
+
=
8
occurs
x
3
=
24
2+4
6
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
+
=
9
occurs
x
2
=
18
1+8
9
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
45
-
-
26
-
126
-
54
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
4+5
-
-
2+6
-
1+2+6
-
5+4
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
9
-
-
8
-
9
-
9
-
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
-
-
-
-
-
-
-
-
-
-
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
9
-
-
8
-
9
-
9

 

 

BEYOND THE VEIL ANOTHER VEIL ANOTHER VEIL BEYOND

 

 

A

HISTORY OF GOD

Karen Armstrong 1993

The God of the Mystics

Page 250

"Perhaps the most famous of the early Jewish mystical texts is the fifth century Sefer Yezirah (The Book of Creation). There is no attempt to describe the creative process realistically; the account is unashamedly symbolic and shows God creating the world by means of language as though he were writing a book. But language has been entirely transformed and the message of creation is no longer clear. Each letter of the Hebrew alphabet is given a numerical value; by combining the letters with the sacred numbers, rearranging them in endless configurations, the mystic weaned his mind away from the normal connotations of words."

 

Page 250

THERE IS NO ATTEMPT MADE TO DESCRIBE THE CREATIVE PROCESS REALISTICALLY THE ACCOUNT

IS UNASHAMEDLY SYMBOLIC AND SHOWS GOD CREATING THE WORLD BY MEANS OF LANGUAGE AS

THOUGH HE WERE WRITING A BOOK. BUT LANGUAGE HAS BEEN ENTIRELY TRANSFORMED AND THE

MESSAGE OF CREATION IS NO LONGER CLEAR EACH LETTER OF THE HEBREW ALPHABET IS GIVEN

A NUMERICAL VALUE BY COMBINING THE LETTERS WITH THE SACRED NUMBERS REARRANGING

THEM IN ENDLESS CONFIGURATIONS THE MYSTIC WEANED THE MIND AWAY FROM THE NORMAL

CONNOTATIONS OF WORDS

 

 

THE LIGHT IS RISING NOW RISING IS THE LIGHT

 

....

 

A
B
C
D
E
F
G
H
I
1
2
3
4
5
6
7
8
9
 =
 =
 =
 =
 =
 =
 =
 =
=
 =
 =
 =
 =
 =
 =
 =
 =
=
J
K
L
M
N
O
P
Q
R
10
11
12
13
14
15
16
17
18
1+0
1+1
1+2
1+3
1+4
1+5
1+6
1+7
1+8
1
2
3
4
5
6
7
8
9
 =
 =
 =
 =
 =
 =
 =
 =
=
 =
 =
 =
 =
 =
 =
 =
 =
=
S
T
U
V
W
X
Y
Z
I
19
20
21
22
23
24
25
26
9
1+9
2+0
2+1
2+2
2+3
2+4
2+5
2+6
ME
1
2
3
4
5
6
7
8
9
 =
 =
 =
 =
 =
 =
 =
 =
=
 =
 =
 =
 =
 =
 =
 =
 =
=
I
ME
I
ME
I
ME
I
ME
I
9
18
9
18
9
18
9
18
9
=
1+8
=
1+8
=
1+8
=
1+8
=
=
9
=
9
=
9
=
9
=
I
ME
I
ME
I
ME
I
ME
1
9
9
9
9
9
9
9
9
9
I
ME
I
ME
I
ME
I
ME
1

 

 

 

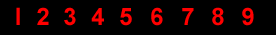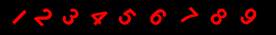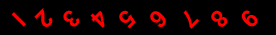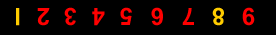
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
-
-
-
-
-
-
-
-
-
1+0
1+1
1+2
1+3
1+4
1+5
1+6
1+7
1+8
1+9
2+0
2+1
2+2
2+3
2+4
2+5
2+6
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z

 

 

 

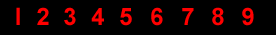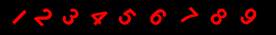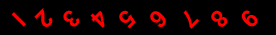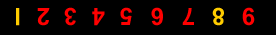
LIGHT AND LIFE

Lars Olof Bjorn 1976

Page 197

"By writing the 26 letters of the alphabet in a certain order one may put down almost any message (this book 'is written with the same letters' as the Encyclopaedia Britannica and Winnie the Pooh, only the order of the letters differs). In the same way Nature is able to convey with her language how a cell and a whole organism is to be constructed and how it is to function. Nature has succeeded better than we humans; for the genetic code there is only one universal language which is the same in a man, a bean plant and a bacterium."

"BY WRITING THE 26 LETTERS OF THE ALPHABET IN A CERTAIN ORDER

ONE MAY PUT DOWN ALMOST ANY MESSAGE"

 

 

"FOR THE GENETIC CODE THERE IS ONLY ONE UNIVERSAL LANGUAGE"

 

DNA AND DNA DNA AND DNA DNA AND DNA

DNA AND DNA DNA AND DNA DNA AND DNA

 

 

 

 

A QUEST FOR THE BEGINNING AND THE END

Graham Hancock 1995

Chapter 32

Speaking to the Unborn

Page 285

"It is understandable that a huge range of myths from all over the ancient world should describe geological catastrophes in graphic detail. Mankind survived the horror of the last Ice Age, and the most plausible source for our enduring traditions of flooding and freezing, massive volcanism and devastating earthquakes is in the tumultuous upheavals unleashed during the great meltdown of 15,000 to 8000 BC. The final retreat of the ice sheets, and the consequent 300-400 foot rise in global sea levels, took place only a few thousand years before the beginning of the historical period. It is therefore not surprising that all our early civilizations should have retained vivid memories of the vast cataclysms that had terrified their forefathers.
Much harder to explain is the peculiar but distinctive way the myths of cataclysm seem to bear the intelligent imprint of a guiding hand.l Indeed the degree of convergence between such ancient stories is frequently remarkable enough to raise the suspicion that they must all have been 'written' by the same 'author'.
Could that author have had anything to do with the wondrous deity, or superhuman, spoken of in so many of the myths we have reviewed, who appears immediately after the world has been shattered by a horrifying geological catastrophe and brings comfort and the gifts of civilization to the shocked and demoralized survivors?
White and bearded, Osiris is the Egyptian manifestation of this / Page 286 / universal figure, and it may not be an accident that one of the first acts he is remembered for in myth is the abolition of cannibalism among the primitive inhabitants of the Nile Valley.2 Viracocha, in South America, was said to have begun his civilizing mission immediately after a great flood; Quetzalcoatl, the discoverer of maize, brought the benefits of crops, mathematics, astronomy and a refined culture to Mexico after the Fourth Sun had been overwhelmed by a destroying deluge.
Could these strange myths contain a record of encounters between scattered palaeolithic tribes which survived the last Ice Age and an as yet unidentified high civilization which passed through the same epoch?
And could the myths be attempts to communicate?

A message in the bottle of time

'Of all the other stupendous inventions,' Galileo once remarked,

what sublimity of mind must have been his who conceived how to communicate his most secret thoughts to any other person, though very distant either in time or place, speaking with those who are in the Indies, speaking to those who are not yet born, nor shall be this thousand or ten thousand years? And with no greater difficulty than the various arrangements of two dozen little signs on paper? Let this be the seal of all the admirable inventions of men.3

If the 'precessional message' identified by scholars like Santillana, von Dechend and Jane Sellers is indeed a deliberate attempt at communication by some lost civilization of antiquity, how come it wasn't just written down and left for us to find? Wouldn't that have been easier than encoding it in myths? Perhaps.
Nevertheless, suppose that whatever the message was written on got destroyed or worn away after many thousands of years? Or suppose that the language in which it was inscribed was later forgotten utterly (like the enigmatic Indus Valley script, which has been studied closely for more than half a century but has so far resisted all attempts at decoding)? It must be obvious that in such circumstances a written / Page 287 / legacy to the future would be of no value at all, because nobody would be able to make sense of it.
What one would look for, therefore, would be a universal language, the kind of language that would be comprehensible to any technologically advanced society in any epoch, even a thousand or ten thousand years into the future. Such languages are few and far between, but mathematics is one of them - and the city of Teotihuacan may be the calling-card of a lost civilization written in the eternal language of mathematics.
Geodetic data, related to the exact positioning of fixed geographical points and to the shape and size of the earth, would also remain valid and recognizable for tens of thousands of years, and might be most conveniently expressed by means of cartography (or in the construction of giant geodetic monuments like the Great Pyramid of Egypt, as we shall see).
Another 'constant' in our solar system is the language of time: the great but regular intervals of time calibrated by the inch-worm creep of precessional motion. Now, or ten thousand years in the future, a message that prints out numbers like 72 or 2160 or 4320or 25,920 should be instantly intelligible to any civilization that has evolved a modest talent for mathematics and the ability to detect and measure the almost imperceptible reverse wobble that the sun appears to make along the ecliptic against the background of the fixed stars..."

"What one would look for, therefore, would be a universal language, the kind of language that would be comprehensible to any technologically advanced society in any epoch, even a thousand or ten thousand years into the future. Such languages are few and far between, but mathematics is one of them"

"WRITTEN IN THE ETERNAL LANGUAGE OF MATHEMATICS"

 

A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
-
-
-
-
-
-
-
-
-
1+0
1+1
1+2
1+3
1+4
1+5
1+6
1+7
1+8
1+9
2+0
2+1
2+2
2+3
2+4
2+5
2+6
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z

 

 

THERE IS NO ATTEMPT MADE TO DESCRIBE THE CREATIVE PROCESS REALISTICALLY

THE ACCOUNT IS SYMBOLIC AND SHOWS GOD CREATING THE WORLD BY MEANS OF LANGUAGE

AS THOUGH WRITING A BOOK BUT LANGUAGE ENTIRELY TRANSFORMED

THE MESSAGE OF CREATION IS CLEAR EACH LETTER OF

THE

ALPHABET

IS

GIVEN

A

NUMERICAL

VALUE BY COMBINING THE LETTERS WITH THE SACRED NUMBERS

REARRANGING THEM IN ENDLESS CONFIGURATIONS

THE MYSTIC WEANED THE MIND AWAY FROM THE NORMAL CONNOTATIONS OF WORDS

 

....

 

THE LIGHT IS RISING NOW RISING IS THE LIGHT

 

 

 

 

26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
8
9
-
-
-
-
5
6
-
-
-
1
-
-
-
-
6
-
8
+
=
43
4+3
=
7
-
7
-
7
-
-
-
-
-
-
-
-
8
9
-
-
-
-
14
15
-
-
-
19
-
-
-
-
24
-
26
+
=
115
1+1+5
=
7
-
7
-
7
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
-
-
1
2
3
4
-
-
7
8
9
-
2
3
4
5
-
7
-
+
=
83
8+3
=
11
1+1
2
-
2
-
1
2
3
4
5
6
7
-
-
10
11
12
13
-
-
16
17
18
-
20
21
22
23
-
25
-
+
=
236
2+3+6
=
11
1+1
2
-
2
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
+
=
351
3+5+1
=
9
-
9
-
9
-
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
+
=
126
1+2+6
=
9
-
9
-
9
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
+
=
1
occurs
x
3
=
3
-
3
-
-
2
-
-
-
-
-
-
-
-
2
-
-
-
-
-
-
-
-
2
-
-
-
-
-
-
+
=
2
occurs
x
3
=
6
-
6
-
-
-
3
-
-
-
-
-
-
-
-
3
-
-
-
-
-
-
-
-
3
-
-
-
-
-
+
=
3
occurs
x
3
=
9
-
9
-
-
-
-
4
-
-
-
-
-
-
-
-
4
-
-
-
-
-
-
-
-
4
-
-
-
-
+
=
4
occurs
x
3
=
12
1+2
3
-
-
-
-
-
5
-
-
-
-
-
-
-
-
5
-
-
-
-
-
-
-
-
5
-
-
-
+
=
5
occurs
x
3
=
15
1+5
6
-
-
-
-
-
-
6
-
-
-
-
-
-
-
-
6
-
-
-
-
-
-
-
-
6
-
-
+
=
6
occurs
x
3
=
18
1+8
9
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
-
7
-
+
=
7
occurs
x
3
=
21
2+1
3
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
8
+
=
8
occurs
x
3
=
24
2+4
6
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
+
=
9
occurs
x
2
=
18
1+8
9
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
45
-
-
26
-
126
-
54
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
4+5
-
-
2+6
-
1+2+6
-
5+4
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
9
-
-
8
-
9
-
9
-
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
-
-
-
-
-
-
-
-
-
-
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
9
-
-
8
-
9
-
9

 

 

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z =351= Z Y X W V U T S R Q P O N M L K J I H G F E D C B A

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z =126= Z Y X W V U T S R Q P O N M L K J I H G F E D C B A

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z =9= Z Y X W V U T S R Q P O N M L K J I H G F E D C B A

 

 

ABCDEFGH I JKLMNOPQ R STUVWXYZ =351= ZYXWVUTS R QPONMLKJ I HGFEDCBA

ABCDEFGH I JKLMNOPQ R STUVWXYZ =126= ZYXWVUTS R QPONMLKJ I HGFEDCBA

ABCDEFGH I JKLMNOPQ R STUVWXYZ =9= ZYXWVUTS R QPONMLKJ I HGFEDCBA

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
A
=
1
-
5
ADDED
18
18
9
-
-
-
-
-
-
-
-
-
9
T
=
2
-
2
TO
35
8
8
-
-
-
-
-
-
-
-
8
-
A
=
1
-
3
ALL
25
7
7
-
-
-
-
-
-
-
7
-
-
M
=
4
-
5
MINUS
76
22
4
-
-
-
-
4
-
-
-
-
-
N
=
5
-
4
NONE
48
21
3
-
-
-
3
-
-
-
-
-
-
S
=
1
-
6
SHARED
55
28
1
-
1
-
-
-
-
-
-
-
-
B
=
2
-
2
BY
27
9
9
-
-
-
-
-
-
-
-
-
9
E
=
5
-
10
EVERYTHING
133
61
7
-
-
-
-
-
-
-
7
-
-
M
=
4
-
10
MULTIPLIED
121
49
4
-
-
-
-
4
-
-
-
-
-
I
=
9
-
2
IN
23
14
5
-
-
-
-
-
5
-
-
-
-
A
=
1
-
9
ABUNDANCE
65
29
2
-
-
2
-
-
-
-
-
-
-
-
-
35
-
58
First Total
995
266
59
-
1
2
3
8
5
6
14
8
18
-
-
3+5
-
5+8
Add to Reduce
9+9+5
2+6+6
5+9
-
-
-
-
-
-
-
1+4
-
1+8
-
-
8
-
13
Second Total
23
14
10
-
1
2
3
8
5
6
5
8
9
-
-
-
-
1+3
Reduce to Deduce
2+3
1+4
1+0
-
-
-
-
-
-
-
-
-
-
-
-
8
-
4
Essence of Number
5
5
5
-
1
2
3
8
5
6
5
8
9

 

 

EVOLVE LOVE EVOLVE

LOVE SOLVES LOVE

EVOLVE LOVE EVOLVE

 

 

 

 

 

 

THE DEATH OF GODS IN ANCIENT EGYPT

Jane B. Sellars 1992

Page 204

"The overwhelming awe that accompanies the realization, of the measurable orderliness of the universe strikes modern man as well. Admiral Weiland E. Byrd, alone In the Antarctic for five months of polar darkness, wrote these phrases of intense feeling:

Here were the imponderable processes and forces of the cosmos, harmonious and soundless. Harmony, that was it! I could feel no doubt of oneness with the universe. The conviction came that the rhythm was too orderly, too harmonious, too perfect to be a product of blind chance - that, therefore there must be purpose in the whole and that man was part of that whole and not an accidental offshoot. It was a feeling that transcended reason; that went to the heart of man's despair and found it groundless. The universe was a cosmos, not a chaos; man was as rightfully a part of that cosmos as were the day and night.10

Returning to the account of the story of Osiris, son of Cronos god of' Measurable Time, Plutarch takes, pains to remind the reader of the original Egyptian year consisting of 360 days.

Phrases are used that prompt simple mental. calculations and an attention to numbers, for example, the 360-day year is described as being '12 months of 30 days each'. Then we are told that, Osiris leaves on a long journey, during which Seth, his evil brother, plots with 72 companions to slay Osiris: He also secretly obtained the measure of Osiris and made ready a chest in which to entrap him.

The, interesting thing about this part of the-account is that nowhere in the original texts of the Egyptians are we told that Seth, has 72 companions. We have already been encouraged to equate Osiris with the concept of measured time; his father being Cronos. It is also an observable fact that Cronos-Saturn has the longest sidereal period of the known planets at that time, an orbit. of 30 years. Saturn is absent from a specific constellation for that length of time.

A simple mathematical fact has been revealed to any that are even remotely sensitive to numbers: if you multiply 72 by 30, the years of Saturn's absence (and the mention of Osiris's absence prompts one to recall this other), the resulting product is 2,160: the number of years required, for one 30° shift, or a shift: through one complete sign of the zodiac. This number multplied by the / Page205 / 12 signs also gives 25,920. (And Plutarch has reminded us of 12)

If you multiply the unusual number 72 by 360, a number that Plutarch mentions several times, the product will be 25,920, again the number of years symbolizing the ultimate rebirth.

This 'Eternal Return' is the return of, say, Taurus to the position of marking the vernal equinox by 'riding in the solar bark with. Re' after having relinquished this honoured position to Aries, and subsequently to the to other zodiacal constellations.

Such a return after 25,920 years is indeed a revisit to a Golden Age, golden not only because of a remarkable symmetry In the heavens, but golden because it existed before the Egyptians experienced heaven's changeability.

But now to inform the reader of a fact he or she may already know. Hipparaus did: not really have the exact figures: he was a trifle off in his observations and calculations. In his published work, On the Displacement of the Solstitial and Equinoctial Signs, he gave figures of 45" to 46" a year, while the truer precessional lag along the ecliptic is about 50 seconds. The exact measurement for the lag, based on the correct annual lag of 50'274" is 1° in 71.6 years, or 360° in 25,776 years, only 144 years less than the figure of 25,920.

With Hipparchus's incorrect figures a 'Great Year' takes from 28,173.9 to 28,800 years, incorrect by a difference of from 2,397.9 years to 3,024.

Since Nicholas Copernicus (AD 1473-1543) has always been credited with giving the correct numbers (although Arabic astronomer Nasir al-Din Tusi,11 born AD 1201, is known to have fixed the Precession at 50°), we may correctly ask, and with justifiable astonishment 'Just whose information was Plutarch transmitting'

AN IMPORTANT POSTSCRIPT

Of course, using our own notational system, all the important numbers have digits that reduce to that amazing number 9 a number that has always delighted budding mathematician.

Page 206

Somewhere along the way, according to Robert Graves, 9 became the number of lunar wisdom.12

This number is found often in the mythologies of the world. the Viking god Odin hung for nine days and nights on the World Tree in order to acquire the secret of the runes, those magic symbols out of which writing and numbers grew. Only a terrible sacrifice would give away this secret, which conveyed upon its owner power and dominion over all, so Odin hung from his neck those long 9 days and nights over the 'bottomless abyss'. In the tree were 9 worlds, and another god was said to have been born of 9 mothers.

Robert Graves, in his White Goddess, Is intrigued by the seemingly recurring quality of the number 72 in early myth and ritual. Graves tells his reader that 72 is always connected with the number 5, which reflects, among other things, the five Celtic dialects that he was investigating. Of course, 5 x 72= 360, 360 x 72= 25,920. Five is also the number of the planets known to the ancient world, that is, Saturn, Jupiter, Mars, Venus Mercury.

Graves suggests a religious mystery bound up with two ancient Celtic 'Tree Alphabets' or cipher alphabets, which as genuine articles of Druidism were orally preserved and transmitted for centuries. He argues convincingly that the ancient poetry of Europe was ultimately based on what its composers believed to be magical principles, the rudiments of which formed a close religious secret for centuries. In time these were-garbled, discredited and forgotten.

Among the many signs of the transmission of special numbers he points out that the aggregate number of letter strokes for the complete 22-letter Ogham alphabet that he is studying is 72 and that this number is the multiple of 9, 'the number of lunar wisdom'. . . . he then mentions something about 'the seventy day season during which Venus moves successively from. maximum eastern elongation 'to inferior conjunction and maximum western elongation'.13

Page 207

"...Feniusa Farsa, Graves equates this hero with Dionysus. Farsa has 72 assistants who helped him master the 72 languages created at the confusion of Babel, the tower of which is said to be built of 9 different materials

We are also reminded of the miraculous translation into Greek of the Five Books of Moses that was done by 72 scholars working for 72 days, Although the symbol for the Septuagint is LXX, legend, according to the fictional letter of Aristeas, records 72. The translation was done for Ptolemy Philadelphus (c.250 BC), by Hellenistic Jews, possibly from Alexandra.14

Graves did not know why this number was necessary, but he points out that he understands Frazer's Golden Bough to be a book hinting that 'the secret involves the truth that the Christian dogma, and rituals, are the refinement of a great body of primitive beliefs, and that the only original element in Christianity- is the personality of Christ.15

Frances A. Yates, historian of Renaissance hermetisma tells, us the cabala had 72 angels through which the sephiroth (the powers of God) are believed to be approached, and further, she supplies the information that although the Cabala supplied a set of 48 conclusions purporting to confirm the Christian religion from the foundation of ancient wisdom, Pico Della Mirandola, a Renaissance magus, introduced instead 72, which were his 'own opinion' of the correct number. Yates writes, 'It is no accident there are seventy-two of Pico's Cabalist conclusions, for the conclusion shows that he knew something of the mystery of the Name of God with seventy-two letters.'16

In Hamlet's Mill de Santillana adds the facts that 432,000 is the number of syllables in the Rig-Veda, which when multiplied by the soss (60) gives 25,920" (The reader is forgiven for a bit of laughter at this point)

The Bible has not escaped his pursuit. A prominent Assyriologist of the last century insisted that the total of the years recounted mounted in Genesis for the lifetimes of patriarchs from the Flood also contained the needed secret numbers. (He showed that in the 1,656 years recounted in the Bible there are 86,400 7 day weeks, and dividing this number yields / Page 208 / 43,200.) In Indian yogic schools it is held that all living beings exhale and inhale 21,600 times a day, multiply this by 2 and again we have the necessary 432 digits.

Joseph Campbell discerns the secret in the date set for the coming of Patrick to Ireland. Myth-gives this date-as-the interesting number of AD.432.18

Whatever one may think-of some of these number coincidences, it becomes difficult to escape the suspicion that many signs (number and otherwise) - indicate that early man observed the results of the movement of Precession and that the - transmission of this information was considered of prime importance.

With the awareness of the phenomenon, observers would certainly have tried for its measure, and such an endeavour would have constituted the construction-of a 'Unified Field Theory' for nothing less than Creation itself. Once determined, it would have been information worthy of secrecy and worthy of the passing on to future adepts.

But one last word about mankind's romance with number coincidences.The antagonist in John Updike's novel, Roger's Version, is a computer hacker, who, convinced, that scientific evidence of God's existence is accumulating, endeavours to prove it by feeding -all the available scientific information. into a comuter. In his search for God 'breaking, through', he has become fascinated by certain numbers that have continually been cropping up. He explains them excitedly as 'the terms of Creation':

"...after a while I noticed that all over the sheet there seemed to hit these twenty-fours Jumping out at me. Two four; two, four. Planck time, for instance, divided by the radiation constant yields a figure near eight times ten again to the negative twenty-fourth, and the permittivity of free space, or electric constant, into the Bohr radius ekla almost exactly six times ten to the negative twenty-fourth. On positive side, the electromagnetic line-structure constant times Hubble radius - that is, the size of the universe as we now perceive it gives us something quite close to ten to the twenty-fourth, and the strong-force constant times the charge on the proton produces two point four times ten to the negative eighteenth, for another I began to circle twenty-four wherever it appeared on the Printout here' - he held it up his piece of stripped and striped wallpaper, decorated / Page 209 / with a number of scarlet circles - 'you can see it's more than random.'19
This inhabitant of the twentieth century is convinced that the striking occurrences of 2 and 4 reveal the sacred numbers by which God is speaking to us.

So much for any scorn directed to ancient man's fascination with number coincidences. That fascination is alive and well, Just a bit more incomprehensible"

 

 

NUMBER

9

THE SEARCH FOR THE SIGMA CODE

Cecil Balmond 1998

Cycles and Patterns

Page 165

Patterns

"The essence of mathematics is to look for patterns.

Our minds seem to be organised to search for relationships and sequences. We look for hidden orders.

These intuitions seem to be more important than the facts themselves, for there is always the thrill at finding something, a pattern, it is a discovery - what was unknown is now revealed. Imagine looking up at the stars and finding the zodiac!

Searching out patterns is a pure delight.

Suddenly the counters fall into place and a connection is found, not necessarily a geometric one, but a relationship between numbers, pictures of the mind, that were not obvious before. There is that excitement of finding order in something that was otherwise hidden.

And there is the knowledge that a huge unseen world lurks behind the facades we see of the numbers themselves."

 

....

 

THE LIGHT IS RISING NOW RISING IS THE LIGHT

 

 

 

 

Y
=
3
-
3
YOU
61
16
7
A
=
1
-
3
ARE
24
15
6
G
=
7
-
5
GOING
52
34
7
O
=
6
-
2
ON
29
11
2
A
=
1
-
1
A
1
1
1
J
=
1
-
7
JOURNEY
108
36
9
A
=
1
-
1
A
1
1
1
V
=
4
-
4
VERY
70
25
7
S
=
1
-
7
SPECIAL
65
29
2
J
=
1
-
7
JOURNEY
108
36
9
D
=
4
-
2
DO
19
10
1
H
=
8
-
4
HAVE
36
18
9
A
=
1
-
1
A
1
1
1
P
=
7
-
8
PLEASANT
88
25
7
J
=
1
-
7
JOURNEY
108
36
9
D
=
4
-
2
DO
19
10
1
``-
-
55
-
54
First Total
790
304
79
-
-
5+5
-
5+4
Add to Reduce
7+9+0
3+0+4
7+9
-
-
10
-
9
Second Total
16
7
16
-
-
1+0
-
-
Reduce to Deduce
1+6
-
1+6
-
-
1
-
9
Essence of Number
7
7
7

 

 

OF TIME AND STARS

Arthur C. Clarke

Page 205

The Sentinel

"I can never look now at the Milky Way without wondering from which of those banked clouds of stars the emissaries are coming. If you will pardon so commonplace a simile, we have set off the fire alarm and have nothing to do but to wait.

I do not think we will have to wait for long.

 

 

I

CAN NEVER LOOK NOW AT THE MILKY WAY WITHOUT WONDERING

FROM WHICH OF THOSE BANKED CLOUDS OF STARS THE EMISSARIES ARE COMING.

IF YOU WILL PARDON SO COMMONPLACE A SIMILE,

WE HAVE SET OFF THE FIRE ALARM AND HAVE NOTHING TO DO BUT TO WAIT.

I DO NOT THINK WE WILL HAVE TO WAIT FOR LONG.

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
I
=
1
-
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
C
=
3
-
3
CAN
18
9
9
-
-
-
-
-
-
-
-
-
9
N
=
5
-
5
NEVER
64
28
1
-
1
-
-
-
-
-
-
-
-
L
=
3
-
4
LOOK
53
17
8
-
-
-
-
-
-
-
-
8
-
N
=
5
-
3
NOW
52
16
7
-
-
-
-
-
-
-
7
-
-
A
=
1
-
2
AT
21
3
3
-
-
-
3
-
-
-
-
-
-
T
=
2
-
3
THE
33
15
6
-
-
-
-
-
-
6
-
-
-
M
=
4
-
5
MILKY
70
25
7
-
-
-
-
-
-
-
7
-
-
W
=
5
-
3
WAY
49
13
4
-
-
-
-
4
-
-
-
-
-
W
=
5
-
7
WITHOUT
116
35
8
-
-
-
-
-
-
-
-
8
-
W
=
5
-
9
WONDERING
109
55
1
-
1
-
-
-
-
-
-
-
-
F
=
6
-
4
FROM
52
25
7
-
-
-
-
-
-
-
7
-
-
W
=
5
-
5
WHICH
51
33
6
-
-
-
-
-
-
6
-
-
-
O
=
6
-
2
OF
21
12
3
-
-
-
3
-
-
-
-
-
-
T
=
2
-
5
THOSE
67
22
4
-
-
-
-
4
-
-
-
-
-
B
=
2
-
6
BANKED
37
19
1
-
1
-
-
-
-
-
-
-
-
C
=
3
-
6
CLOUDS
74
20
2
-
-
2
-
-
-
-
-
-
-
O
=
6
-
2
OF
21
12
3
-
-
-
3
-
-
-
-
-
-
S
=
1
-
5
STARS
77
14
5
-
-
-
-
-
5
-
-
-
-
T
=
2
-
3
THE
33
15
6
-
-
-
-
-
-
6
-
-
-
E
=
5
-
10
EMISSARIES
117
45
9
-
-
-
-
-
-
-
-
-
9
A
=
1
-
3
ARE
24
15
6
-
-
-
-
-
-
6
-
-
-
C
=
3
-
6
COMING
61
34
7
-
-
-
-
-
-
-
7
-
-
-
-
89
-
102
First Total
1229
491
122
-
3
2
9
8
5
24
28
16
27
-
-
8+9
-
1+0+2
Add to Reduce
1+2+2+9
4+9+1
1+1+2
-
-
-
-
-
-
2+4
2+8
1+6
2+7
-
-
17
-
3
Second Total
14
14
5
-
3
2
9
8
5
6
10
7
9
-
-
1+7
-
-
Reduce to Deduce
1+4
1+4
-
-
-
-
-
-
-
-
1+0
-
-
-
-
8
-
3
Essence of Number
5
5
5
-
3
2
9
8
5
6
1
7
9

 

I

CAN NEVER LOOK NOW AT THE MILKY WAY WITHOUT WONDERING

FROM WHICH OF THOSE BANKED CLOUDS OF STARS THE EMISSARIES ARE COMING

 

 

IF YOU WILL PARDON SO COMMONPLACE A SIMILE,

WE HAVE SET OFF THE FIRE ALARM AND HAVE NOTHING TO DO BUT TO WAIT.

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
I
=
9
-
2
IF
15
15
6
-
-
-
-
-
-
6
-
-
-
Y
=
7
-
3
YOU
61
16
7
-
-
-
-
-
-
-
7
-
-
W
=
5
-
4
WILL
56
20
2
-
-
2
-
-
-
-
-
-
-
P
=
7
-
6
PARDON
68
32
5
-
-
-
-
-
5
-
-
-
-
S
=
1
-
2
SO
34
7
7
-
-
-
-
-
-
-
7
-
-
C
=
3
-
11
COMMONPLACE
110
47
2
-
-
2
-
-
-
-
-
-
-
A
=
1
-
1
A
1
1
1
-
1
-
-
-
-
-
-
-
-
S
=
1
-
6
SIMILE
67
31
4
-
-
-
-
4
-
-
-
-
-
W
=
5
-
2
WE
28
10
1
-
1
-
-
-
-
-
-
-
-
H
=
8
-
4
HAVE
36
18
9
-
-
-
-
-
-
-
-
-
9
S
=
1
-
2
SET
44
8
8
-
-
-
-
-
-
-
-
8
-
O
=
6
-
2
OFF
27
18
9
-
-
-
-
-
-
-
-
-
9
T
=
2
-
3
THE
33
15
6
-
-
-
-
-
-
6
-
-
-
F
=
6
-
4
FIRE
38
29
2
-
-
2
-
-
-
-
-
-
-
A
=
1
-
5
ALARM
45
18
9
-
-
-
-
-
-
-
-
-
9
A
=
1
-
3
AND
19
10
1
-
1
-
-
-
-
-
-
-
-
H
=
8
-
4
HAVE
36
18
9
-
-
-
-
-
-
-
-
-
9
N
=
5
-
7
NOTHING
87
42
6
-
-
-
-
-
-
6
-
-
-
T
=
2
-
2
TO
35
8
8
-
-
-
-
-
-
-
-
8
-
D
=
4
-
2
DO
19
10
1
-
1
-
-
-
-
-
-
-
-
B
=
2
-
3
BUT
43
7
7
-
-
-
-
-
-
-
7
-
-
T
=
2
-
2
TO
35
8
8
-
-
-
-
-
-
-
-
8
-
W
=
5
-
4
WAIT
53
17
8
-
-
-
-
-
-
-
-
8
-
-
-
54
-
60
First Total
990
405
126
-
4
6
3
4
5
18
21
32
36
-
-
5+4
-
6+0
Add to Reduce
9+9+0
4+0+5
1+2+6
-
-
-
-
-
-
1+8
2+1
3+2
3+6
-
-
9
-
3
Second Total
18
9
9
-
4
6
3
4
5
9
3
5
9
-
-
-
-
-
Reduce to Deduce
1+8
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
-
3
Essence of Number
9
9
9
-
4
6
3
4
5
9
3
5
9

 

 

I DO NOT THINK WE WILL HAVE TO WAIT FOR LONG

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
I
=
1
-
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
D
=
4
-
2
DO
19
10
1
-
1
-
-
-
-
-
-
-
-
N
=
5
-
2
NOT
49
13
4
-
-
-
-
4
-
-
-
-
-
T
=
2
-
2
THINK
62
26
8
-
-
-
-
-
-
-
-
8
-
W
=
5
-
2
WE
28
10
1
-
1
-
-
-
-
-
-
-
-
W
=
5
-
4
WILL
56
20
2
-
-
2
-
-
-
-
-
-
-
H
=
8
-
4
HAVE
36
18
9
-
-
-
-
-
-
-
-
-
9
T
=
2
-
2
TO
35
8
8
-
-
-
-
-
-
-
-
8
-
W
=
5
-
4
WAIT
53
17
8
-
-
-
-
-
-
-
-
8
-
F
=
6
-
2
FOR
39
21
3
-
-
-
3
-
-
-
-
-
-
L
=
3
-
3
LONG
48
21
3
-
-
-
3
-
-
-
-
-
-
-
-
54
-
34
First Total
434
173
56
-
2
2
6
4
5
6
7
24
18
-
-
5+4
-
3+4
Add to Reduce
4+3+4
1+7+3
5+6
-
-
-
-
-
-
-
-
2+4
1+8
-
-
9
-
7
Second Total
11
11
11
-
2
2
6
4
5
6
7
6
9
-
-
-
-
-
Reduce to Deduce
1+1
1+1
1+1
-
-
-
-
-
-
-
-
-
-
-
-
9
-
7
Essence of Number
2
2
2
-
2
2
6
4
5
6
7
6
9

 

 

 

IN OUR TIME

Last broadcast on Thu, 18 Dec 2003, 21:30 on BBC Radio 4

"Melvyn Bragg and guests discuss the feat of astonishing intellectual engineering which provides us with millions of words in hundreds of languages. At the start of the twentieth century, in the depths of an ancient Egyptian turquoise mine on the Sinai peninsular, an archaeologist called Sir Flinders Petrie made an exciting discovery. Scratched onto rocks, pots and portable items, he found scribblings of a very unexpected but strangely familiar nature. He had expected to see the complex pictorial hieroglyphic script the Egyptian establishment had used for over 1000 years, but it seemed that at this very early period, 1700 BC, the mine workers and Semitic slaves had started using a new informal system of graffiti, one which was brilliantly simple, endlessly adaptable and perfectly portable: the Alphabet. This was probably the earliest example of an alphabetic script and it bears an uncanny resemblance to our own.

Did the alphabet really spring into life almost fully formed? How did it manage to conquer three quarters of the globe? And despite its Cyrillic and Arabic variations and the myriad languages it has been used to write, why is there essentially only one alphabet anywhere in the world?"

 

 

THE FIFTH ELEMENT

A Novel By Terry Bisson

From The Screenplay By Luc Besson & Robert Mark Kamen

Based On a Story By Luc Besson

THE FIFTH ELEMENT

A Film By Luc Besson

Page 14

“the Fifth Element,” whispered the priest, his words as soft as a prayer.

Page 133

Pop!

Pop!

Pop!

Page 242

“He struck the match
A
tiny flame appeared . . .
sputtered . . .
flickered . . .
Dead silence gripped the room as Korben approached the stone with the tiny flickering match.

Loc Rhod, David and Father Cornelius stood stock still, like statues.
Leeloo lay languidly on the altar.
Cupping the tiny flame! in his ham-sized hand, Korben tiptoed towards the fourth stone.
Pop Pop Pop!
A patch of fire appeared within the stone, and a bright red beam flashed out, joining the yellow, the green and the blue beams on the ceiling of the temple.”

Okay! Finished!" Leeloo said.

She was speaking English? Korben looked at her in amazement.

"Finished what?"

Learning languages." She switched off the computer.

"You mean . . . English?"

She nodded. "All nine hundred!"

Korben was amazed. "You learned all nine hundred Earth languages in just five minutes?.

"Yes! Now it's your turn. I learned your language; you have to learn mine."

 

I
=
9
-
3
I
9
9
9
M
=
4
-
2
ME
18
18
9
E
=
5
-
4
EGO
27
18
9
O
=
6
-
3
OGRE
45
27
9
C
=
3
-
2
CENTRIC
72
27
9
C
=
3
-
3
CONSCIENCE
90
45
9
G
=
7
-
2
GODS
45
18
9
D
=
4
-
4
DIVINE
63
36
9
T
=
1
-
3
THOUGHT
99
36
9

 

 

THE SIRIUS MYSTERY

Robert K.G.Temple 1976

Page 82

The Sacred Fifty

"We must return to the treatise 'The Virgin of the World'. This treatise is quite explicit in saying that Isis and Osiris were sent to help the Earth by giving primitive mankind the arts of civilization:
And Horus thereon said:

'How was it, mother, then, that Earth received God's Efflux?' And Isis said:

'I may not tell the story of (this) birth; for it is not permitted to describe the origin of thy descent, O Horus (son) of mighty power, lest afterwards the way-of-birth of the immortal gods should be known unto men - except so far that God the Monarch, the universal Orderer and Architect, sent for a little while thy mighty sire Osiris, and the mightiest goddess Isis, that they might help the world, for all things needed them.
'Tis they who filled life full of life. 'Tis they who caused the savagery of mutual slaughtering of men to cease. 'Tis they who hallowed precincts to the Gods their ancestors and spots for holy rites. 'Tis they who gave to men laws, food and shelter.'

"Page 73

A Fairy Tale

'I INVOKE THEE, LADY ISIS, WITH WHOM THE GOOD DAIMON DOTH UNITE,

HE WHO IS LORD IN THE PERFECT BLACK.'

 

 

-
-
-
-
-
BLACK RITE
-
-
-
B
=
2
-
5
BLACK
29
11
2
R
=
9
-
4
RITE
52
25
7
-
-
11
Q
9
BLACK RITE
81
36
9
-
-
1+1
-
-
-
8+1
3+6
-
-
-
2
-
9
BLACK RITE
9
9
9

 

 

THE SIRIUS MYSTERY

Robert K.G.Temple 1976

Page 74

"Mead quotes an Egyptian magic papyrus, this being an uncontested Egyptian document which he compares to a passage in the Trismegistic literature: 'I invoke thee, Lady Isis, with whom the Good Daimon doth unite, He who is Lord in the perfect black. '37
We know that Isis is identified with Sirius A, and here we may have a / Page 74 / description of her star-companion 'who is Lord in the perfect black', namely the invisible companion with whom she is united, Sirius B.
Mead, of course, had no inkling of the Sirius question. But he cited this magic papyrus in order to shed comparative light on some extraordinary passages in a Trismegistic treatise he translated which has the title 'The Virgin of the World'. In his comments on the magic papyrus Mead says: 'It is natural to make the Agathodaimon ("the Good Daimon") of the Papyrus refer to Osiris; for indeed it is one of his most frequent designations. Moreover, it is precisely Osiris who is pre-eminently connected with the so-called "under­world", the unseen world, the "mysterious dark". He is lord there. . . and indeed one of the ancient mystery-sayings was precisely, "Osiris is a dark God." ,
'The Virgin of the World' is an extraordinary Trismegistic treatise in the form of a dialogue between the hierophant (high priest) as spokesman for Isis and the neophyte who represents Horus. Thus the priest instructing the initiate is portrayed as Isis instructing her son Horus.
The treatise begins by claiming it is 'her holiest discourse' which 'so speaking Isis doth pour forth'. There is, throughout, a strong emphasis on the hierarchical principle of lower and higher beings in the universe - that earthly mortals are presided over at intervals by other, higher, beings who interfere in Earth's affairs when things here become hopeless, etc. Isis says in the treatise: 'It needs must, therefore, be the less should give place to the greater mysteries.' What she is to disclose to Horus is a great mystery. Mead describes it as the mystery practised by the arch-hierophant. It was the degree (here 'degree' is in the sense of 'degree' in the Masonic 'mysteries', which are hopelessly garbled and watered-down versions of genuine mysteries of earlier times) 'called the "Dark Mystery" or "Black Rite". It was a rite performed only for those who were judged worthy of it after long probation in lower degrees, something of a far more sacred character, apparently, than the instruction in the mysteries enacted in the light.'
Mead adds: 'I would suggest, therefore, that we have here a reference to the most esoteric institution of the Isiac tradition. . .', Isiac meaning of course 'Isis-tradition', and not to be confused with the Book of Isaiah in the Bible (so that perhaps it is best for us not to use the word-form 'Isiac').
It is in attempting to explain the mysterious 'Black Rite' of Isis at the highest degree of the Egyptian mysteries that Mead cited the magic papyrus which I have already quoted. He explains the 'Black Rite' as being connected with Osiris being a 'dark god' who is 'Lord of the perfect black' which is 'the unseen world, the mysterious black'.
This treatise 'The Virgin of the World' describes a personage called Hermes who seems to represent a race of beings who taught earthly mankind the arts of civilization after which: 'And thus, with charge unto his kinsmen of the Gods to keep sure watch, he mounted to the Stars'.
According to this treatise mankind have been a troublesome lot requiring scrutiny and, at rare intervals of crisis, intervention.
After Hermes left Earth to return to the stars there was or were in Egypt someone or some people designated as 'Tat' (Thoth) who were initiates into the celestial mysteries."

Page 77

"Bearing these books in mind (and I am sure they are there waiting under­ground like a time bomb for us), it is interesting to read this passage in 'TheVirgin of the World' following shortly upon that previously quoted:
The sacred symbols of the cosmic elements were hid away hard by the secrets of Osiris. Hermes, ere he returned to Heaven, invoked a spell on them, and spake these words: . . . 'O holy books, who have been made by my immortal hands, by incorruption's magic spells. . . (at this point there is a lacuna as the text is hopeless) . . . free from decay throughout eternity remain and incorrupt from time! Become unseeable, unfindable, for every one whose foot shall tread the plains of this land, until old Heaven doth bring forth meet instruments for you, whom the Creator shall call souls.'
Thus spake he; and, laying spells on them by means of his own works, he shut them safe away in their own zones. And long enough the time has been since they were hid away.
In the treatise the highest objective of ignorant men searching for the truth
is described as: '(Men) will seek out. . . the inner nature of the holy spaces which no foot may tread, and will chase after them into the height, desiring to observe the nature of the motion of the Heaven.
'These are as yet moderate things. For nothing more remains than Earth's remotest realms; nay, in their daring they will track out Night, the farthest Night of all.'..."

Page 82

"We must note Stecchini's remarks about Delphi as follows :38
The god of Delphi, Apollo, whose name means 'the stone', was identified with an object, the omphalos, 'navel', which has been found. It consisted of an ovoidal stone. . . . The omphalos of Delphi was similar to the object which represented the god Amon in Thebes, the 'navel' of Egypt. In 1966 I presented to the annual meeting of the Archaeological Institute of America a paper in which I maintained that historical accounts, myths, and legends, and some monuments of Delphi, indicate that the oracle was established there by the Pharaohs of the Ethiopian Dynasty.

 

ORACLE = 9
THE ORACLE OF DELPHI = 9
NECHUNG ORACLE = 9
OMPHALOS = 9
NAVEL OF THE WORLD = 9

 

 

-
-
-
-
-
DYNASTY
-
-
-
-
-
2
-
5
D+Y+N+A
44
17
8
-
-
9
-
4
S
19
10
1
-
-
2
-
5
T+Y
45
9
9
B
=
11
Q
9
DYNASTY
108
36
18
-
-
1+1
-
-
-
1+0+8
3+6
1+8
-
-
2
-
9
DYNASTY
9
9
9

 

 

O
=
6
-
-
OSIRIS
-
-
-
-
-
-
-
1
O
15
6
6
-
-
-
-
1
S
19
10
1
-
-
-
-
1
I
9
9
9
-
-
-
-
1
R
18
9
9
-
-
-
-
1
I
9
9
9
-
-
-
-
2
S
19
10
1
O
=
6
Q
6
OSIRIS
89
53
26
-
-
-
-
-
-
8+9
5+3
2+6
O
=
6
-
6
OSIRIS
17
8
8
-
-
-
-
-
-
1+7
-
-
O
=
6
-
6
OSIRIS
8
8
8

 

OSIRIS 89 8x9 72 8x9 89 OSIRIS

 

O
=
6
-
-
OSIRIS
-
-
-
-
-
-
-
2
SO
34
16
7
-
-
-
-
1
I
9
9
9
-
-
-
-
1
R
18
9
9
-
-
-
-
2
IS
28
19
1
O
=
6
Q
6
OSIRIS
89
53
26
-
-
-
-
-
-
8+9
5+3
2+6
O
=
6
-
6
OSIRIS
17
8
8
-
-
-
-
-
-
1+7
-
-
O
=
6
-
6
OSIRIS
8
8
8

 

SIRIUSOSIRISISISISIRISISTERIS

 

 

I

ME

SOS SIGNALS SOS

COMETH FORTH COMETH

MAYDAY MAYDAY MAYDAY

REVEAL O I O REVEAL

THAT THAT THAT

ISISIS

WHAT IS THE NATURE OF THE LIFE FORM SOUNDING THE

OM TONE SACRED NOTE OM

THE ANSWER ANWERS IT IS THE E IN PLANET EARTH THAT IS THE LIFE FORM TRANSMTTING THE

SOS MAYDAY SOS

ALARM CALL ALARM

SEE SAID THE SEER THE BLU E PLANET ITSELF SINGS ITS SONG WITHIN THE SENSE OF COMING DESTINY

 

 

O
=
6
-
-
OSIRIS
-
-
-
-
-
-
-
1
O
15
6
6
-
-
-
-
1
IS
28
19
1
-
-
-
-
1
R
18
9
9
-
-
-
-
2
1S
19
19
1
O
=
6
Q
6
OSIRIS
89
53
26
-
-
-
-
-
-
8+9
5+3
2+6
O
=
6
-
6
OSIRIS
17
8
8
-
-
-
-
-
-
1+7
-
-
O
=
6
-
6
OSIRIS
8
8
8

 

 

-
CHRIST
-
-
-
-
C
3
3
3
-
RISH
54
27
9
-
T
20
2
2
6
CHRIST
77
32
14
-
-
7+7
3+2
1+4
6
CHRIST
14
5
5

 

 

THE USBORNE BOOK OF

FACTS AND LISTS

Lynn Bressler (no date)

Page 82

10 most spoken languages
Chinese 700,000,000 English 400,000,000 Russian 265,000,000 Spanish 240,000,000 Hindustani 230,000,000 Arabic 146,000,000 Portuguese 145,000,000 Bengali 144,000,000 German 119,000,000 Japanese 116,000,000

The first alphabet
The Phoenicians, who once lived where Syria, Jordan and Lebanon are today, had an alphabet of 29 letters as early as 1,700 BC. It was adopted by the Greeks and the Romans. Through the Romans, who went on to conquer most of Europe, it became the alphabet of Western countries.

Sounds strange
One tribe of Mexican Indians hold entire conversations just by whistling. The different pitches provide meaning.

The Rosetta Stone
 The Rosetta Stone was found by Napoleon in the sands of Egypt. It dates to about 196 BC.
On it is an inscription in hieroglyphics and a translation in Greek. , Because scholars knew ancient Greek, they could work out what the Egyptian hieroglyphics meant. From this they learned the language of the ancient Egyptians.

Did You KnowMany Chinese cannot understand each other. They have different ways of speaking (called dialects) in different
parts of the country. But today in schools allover China, the children are being taught one dialect (Mandarin), so that one day all Chinese will understand each other.

Translating computers
Computers can be used to help people of different nationalities, who do not know each others' language, talk to each other. By giving a computer a message in one language it will translate it into another specified language.

Worldwide language
English is spoken either as a first or second language in at least 45 countries. This is more than any other language. It is the language of international business and scientific conferences and is used by airtraffic controllers worldwide. In all, about one third of the world speaks it.

Page 83

Earliest writing Chinese writing has been found on pottery, and even on a tortoise shell, going back 6,000 years. Pictures made the basis for their writing, each picture showing an object or idea. Probably the earliest form of writing came from the Middle East, where Iraq and Iran are now. This region was then ruled by the Sumerians.

The most words

English has more words in it than any other language. There are about1 million in all, a third of which are technical terms. Most
people only use about 1 per cent of the words available, that is, about 10,000. William Shakespeare is reputed to have made most use of the English vocabulary.

A scientific word describing a process in the human cell is 207,000 letters long. This makes this single word equal in length to a short novel or about 80 typed sheets of A4 paper.

Many tongues
A Frenchman, named Georges Henri Schmidt, is fluent (meaning he reads and writes well) in 31 different languages.

International language
Esperanto was invented in the 1880s by a Pole, Dr Zamenhof. It was hoped that it would become the international language of Europe. It took words from many European countries and has a very easy grammar that can be learned in an hour or two.
The same language

The languages of India and Europe may originally come from just one source. Many words in different languages sound similar. For example, the word for King in Latin is Rex, in Indian, Raj, in Italian Re, in French Roi and in Spanish Rey. The original language has been named Indo-European. Basque, spoken in the French and Spanish Pyrenees, is an exception. It seems to have a different source which is still unknown.

Number of alphabets
There are 65 alphabets in use in the world today. Here are some of them: Roman
ABCDEFGHUKLMNOPQRS Greek  Russian (Cyrillic) Hebrew  Chinese (examples omitted)

 

 

Daily Mail, Monday, December 21, 2015

Page 45

ANSWERS TO CORRESPONDENTS
Charles Legge.

QUESTION If E is the most used letter of our alphabet, in what order of usage are the remaining 25 letters?

CODEBREAKERS are especially interested in frequency analysis. The most basic encryption text is achieved by simply replacing one letter by another. So to decipher such an encryption, it's useful to get a frequency count of all the letters. The most frequent letter might represent the most common letter in English, E followed by T, A, 0 and I. The least frequent are Q, Z and X.
Common percentages in standard Englist are: e 12.7, t 9.1, a 8.2, o 7.5, i 7.0, n 6.7, s 6.3 h 6.1, r 6.0, d 4.3, I 4.0, u 2.8, c 2.8, m 2.4, IA 2.4, f 2.2, y 2.0, g 2.0, p 1.9, b 1.5, v 1.0, k 0.8 x 0.2, j 0.2, q 0.1, z 0.1. The top 12 letter: constitute about 80 per cent of the total usage. The top eight letters constitute about 65 per cent of total use.
Codebreakers also look for common pairings, for example the consonants TE and vowels EA. Other pairings are OF, TO IN, IT, IS, BE, AS, AT, SO, WE, HE, BY, OR ON, DO, IF, ME, MY, UP. Common pairs of repeated letters are SS, EE, TT, FF, LL MM and 00. Common triplets are THE EST, FOR, AND, HIS, ENT and THA. The use of letter frequencies and frequency analysis plays a fundamental role in cryptograms and word puzzle games such as Hangman and Scrabble. An example of applying the knowledge of English letter frequency to solving cryptogram is found in Edgar Allan Poe's famous story The Gold-Bug, where the method is successfully applied to decipher a message instructing on the whereabouts of a treasure hidden by Captain Kidd.
A. D. Butler Warrington, Cheshire.

 

 

DAILY MAIL

Monday, October 8, 2007

Harry Bingham

Page 15

"YOU SAY POTATO, I SAY GHOUGHBTEIGHPTEAU !"

"...Yes you CAN spell potato like that. It's one of the amazing quirks which make English the world's dominant language

 

"ABOUT three years ago I started researching a book, This Little Britain, about the various ways in which we Brits have a history .
of being the exception.
In areas such as law, government, economics, agriculture and science, we've often been a uniquely British exception to a general European rule.
Ditto, in such things as men's fashion, Victorian sewers, drunken yobbishness, and - not least - in the whole area of language and literature.
Take spellings. George Bernard Shaw famously commented that English spelling would allow you to write the word 'fish' as 'ghoti' - and it would sound the same (in the latter, the sound 'f' would be from 'gh', as in 'rough'; 'i' would be from 'o' in 'women' and 'sh' as in 'ti' from 'nation').
But he couldn't have been trying all that hard, if that was the best example he came up with. How about 'potato' as in
'ghoughbteighpteau'? That's the sound 'p' as in hiccough, 'o' as in though, 't' as in debt, 'a' as in neighbour, 't' as in ptomaine, 'o' as in bureau. The fact is that with just 26 letters and 48 different sounds to cope with, there were always going to be problems. :
Throw in other pronunciation changes and an appetite for foreign borrowings, and it's no surprise that English has some of the most dangerously unpredictable spellings in the world.
If our spellings are painful, however, our grammar has its blessedly simple side. French nouns are either masculine or feminine; French verbs vary with every puff of the syntactical breeze.
But French is a pretty simple language. Italian has 50 different forms for every verb, ancient Greek more than 300, modern Turkish an eye popping two million. English, by contrast, has just four verb forms (bark, barks, barking, barked), two noun forms (dog, dogs), and just one adjectival form (snappy), thus making our language about the least inflected in the world.
If that's a curious fact, the reason why is perhaps odder still. Back in Alfred the Great's England, two language communities - English and Danish - inter­mingled. Each community could make out the basic words of the other language.

FOR example, the word 'horse' is 'hors' in Old English, 'hossit' in Old Norse. But all those tricksy little word endings would have made no sense at all. So they began to vanish.
Under pressure of trade, friendship and intermarriage, our ancient ancestors did away with inflections almost completely. Confusing at the time, no doubt, but a blessing for those who need to learn the language today.
And there are plenty of people learning it, of course. With about one-and a-half billion non-native speakers, English has become the world's own language - one that accounts for two-thirds of internet content, and a still larger proportion of the world's scientific and technical journals.
It's sometimes suggested that English has achieved its leadership because it's thelanguage of Shakespeare, . because of its unique and beautiful literature.
That's nonsense, of course. English dominates because the British Isles exported English speakers and gunboats in the 19th century, and because America exported Hollywood, GIs and hamburgers in the 20th.
If those Mayflower settlers had chanced to speak Ubykh (a Caucasian language with 81 consonants and 'three vowels) or Rotokas (a Papua New Guinea language with just six consonants and five vowels), the world would most likely be speaking those fine languages today.
Such dominance has its down­side, of course. There are now about 6,800 languages left in the world, compared with perhaps twice that number back at the dawn of agriculture. The remaining languages are now dying at the rate of about one a fortnight.
English is big in other ways too. If you wanted to learn all the words in the Oxford English Dictionary, you'd have to deal with about 500,000 of them (ending with zyxt, a splendid last word by any standards and an archaic Kentish term for thou seest).
Having done that, you'd probably be a bit taken aback to learn the equivalent American dictionary, Webster's, offers a further 450,000 words or so, of which only about half are to be found in the OED, suggesting a pooled total word count of about 750,000.
But there are lots of words that never get in to either dictionary. Flora and fauna are mostly out. So are most acronyms, slang and dialect. Total that lot up and you'd get to a million or so. Next, you'd need to deal with scientific and technological terms, adding another million or so words.
Otherlanguages-can't keep up. The official dictionary-based word count of German is fewer than 200,000. The French word­count is fewer than 100,000. The scale of our vocabulary is impossible to explain, except by recognising that English users are reckless adopters and inventors.
In the cultural realm, however, mere size is hardly likely to impress. In tenus of Nobel Prizes for literature, the United Kingdom trots home in the bronze medal position (beaten by gold­medallist France, and the silver­gong-holder, the US.).
If, on the other hand, you were looking at the total amount of literatureproduced by the British Isles then we would come in level with France, with 13 prizes.

BUT perhaps that's to measure things the wrong way. If you look at Nobel Prizes by language, then English wins by a country mile 26 laureates vs 13 for France).

More to the point, the Nobel Prize Committee is just that: a committee. Wouldn't it be better to let the world's reading public determine which literature it favours? Alas, there are no reliable global sales figures available.
We do, however, have an index of which authors have written the most translated books. British authors romp home in four of the top five places: Agatha Christie in first, then Enid Blyton, Shakespeare and Barbara Cartland in third to fifth. (The one interloper, Frenchman Jules Verne, is in second place.)
Looking more broadly, British authors dominate the top 40, with some 14 authors on the list, compared with 11 for the United States, and 15 for the entire rest of the world put together.
The obvious conclusion: that we Brits have some natural affinity for words and literature, the way that the Germans 'do' music, or the French 'do' visual art.
Such things run both deep and ancient. The vernacular literature of Alfred the Great's England was the most developed in Europe. It's perhaps not surprising that the same is arguably still true today."

 

"YOU SAY POTATO, I SAY GHOUGHBTEIGHPTEAU !"

 

"How about 'potato' as in
'ghoughbteighpteau'?"

 

-
GHOUGHBTEIGHPTEAU
-
-
-
2
G+H
15
15
6
2
O+U
36
9
9
2
G+H
15
15
6
3
B+T+E
27
9
9
1
I
9
9
9
2
G+H
15
15
6
2
P+T
36
9
9
3
E+A+U
27
9
9
17
GHOUGHBTEIGHPTEAU
180
90
63
1+7
-
1+8+0
9+0
6+3
8
GHOUGHBTEIGHPTEAU
9
9
9

 

 

INDIA I AND I INDIA

 

Amazon.com Apple iBookstore Barnes & Noble

Lord Kapila is a renowned sage and the author of the philosophical system known as Sankhya, which forms an important part of India's ancient philosophical heritage.

Sankhya is a system of metaphysics that deals with the elemental principles of the universe; it is also a system of spiritual knowledge, with its own methodology, and culminates in full consciousness of the Supreme Absolute.

Lord Kapila, however, is not an ordinary philosopher or sage but an incarnation of God.

This book deals with his answers to his mother's enquiry about how to overcome ignorance and delusion and attain spiritual enlightenment.

 

 

LORD KAPILA 99-45-9 9-45-99 KAPILA LORD

KAPILA 50-23-5 5-23-50 KAPILA

DEVAHUTI 90-36-9 9-36-90 DEVAHUTI

 

 

Teachings of Lord Kapila | Krishna.com

krishna.com/books/teachings-of-lord-kapila

Lord Kapila's answers to his mother's inquiry about how to overcome ignorance and attain spiritual enlightenment. Lord Kapila is a renowned sage and the ...

Teachings of Lord Kapila

The Son of Devahuti

Lord Kapila's answers to his mother's inquiry about how to overcome ignorance and attain spiritual enlightenment.

Lord Kapila is a renowned sage and the author of the philosophical system known as Sankhya, which forms an important part of India's ancient philosophical heritage.

Sankhya is a system of metaphysics that deals with the elemental principles of the universe; it is also a system of spiritual knowledge, with its own methodology, and culminates in full consciousness of the Supreme Absolute.

Lord Kapila, however, is not an ordinary philosopher or sage but an incarnation of God.

This book deals with his answers to his mother's enquiry about how to overcome ignorance and delusion and attain spiritual enlightenment.

The underlying theme running throughout his answers and throughout Srila Prabhupada's commentaries on them is that one can achieve this goal by practicing bhakti-yoga, the process of linking one's heart to the Lord's heart through loving devotional service.

This series, with original Sanskrit, translations, and purports, sheds light on such topics as the significance of the guru, the psychology of consciousness, the characteristics of a self-realized person, the science of meditation, the nature of transcendental knowledge, and the process of ultimate liberation.

 

 

THE GUINNESS ENCYCLOPEDIA

John Foley

1993

ALPHABETOLOGY

SIGNS AND SYMBOLS

Page 22

The most commonly used numerical symbols throughout the modern World; the so-called Arabic numerals

1 2 3 4 5 6 7 8 9

derive ultimately from a system developed by the Hindus in India sometime between the 3rd Century B,C. and 6th Century A.D.

The more rounded Western Arabic numerals were introduced into Spain by the Moors in the 10th Century.

The first European to take serious note of the new numeration was the French scholar Gerbert of Aurilliac (Pope Sylvester II from 999 to 1003) who had studied the system in Spain

The Hindus are also credited with the invention at some unknown date of the symbol for zero, which was first written as a small circle and later reduced to a large dot.

The nine Indian figures are : 9 8 7 6 5 4 3 2 1

With these nine figures and with the sign O any number may be written.

Leonardo of Pisa

Liber abaci

 

 

1234 5 6789

ONE TWO THREE FOUR 5FIVE5 SIX SEVEN EIGHT NINE

1234 5 6789 9876 5 4321

NINE EIGHT SEVEN SIX 5FIVE5 FOUR THREE TEO ONE

9876 5 4321

 

 

-
LOVE
-
-
-
2
L+O
27
9
9
2
V+E
27
9
9
4
LOVE
54
18
18
-
-
5+4
1+8
1+8
4
LOVE
9
9
9
-
-
-
-
-
-
-
-
-
-
-
EVOLVE
-
-
-
2
E+V
27
9
9
2
O+L
27
9
9
2
V+E
27
9
9
6
EVOLVE
81
27
27
-
-
8+1
2+7
2+7
6
EVOLVE
9
9
9

 

 

THE LOST LANGUAGE OF SYMBOLISM

Harold Bayley

The Lost Language of Symbolism: An Inquiry into the Origin of Certain Letters,

Words, Names, Fairy-Tales, Folklore, and Mythologies. 2 vol. 1912

Page 41

"Mysticism has universally taught that every man has within himself the germs or seeds of Divinity, and that by self-conquest these sparks of Heaven may be fanned into a flame, the flame into a fire, the fire into a star, and the star into a sun."

 

 

THE LOST LANGUAGE OF SYMBOLISM

Harold Bayley

The Lost Language of Symbolism: An Inquiry into the Origin of Certain Letters,

Words, Names, Fairy-Tales, Folklore, and Mythologies. 2 vol. 1912

INTRODUCTION

"... Although etymologists are agreed that language is fossil poetry and that the creation of every word was originally a poem embodying a bold metaphor or a bright conception, it is quite unrealised how close and intimate a relation exists between symbolism and philology. But, as Renouf points out, " It is not improbable that the cat, in Egyptian Mau, became the symbol of the Sun-God or Day, because the word Mau also means light." 1 Renouf likewise notes that not only was RA the name of the Sun-God, but that it was also the usual Egyptian word for Sun. Similarly the Goose, one of the symbols of SEB, was called a Seb ; the Crocodile, one of the symbols of SEBEK, was called a Sebek; the Ibis, one of the symbols of TECHU, was called a Techu ; and the Jackal, one of the symbols of ANPU (ANUBIS), was called an Anpu.
Parallels to this Egyptian custom are also traceable in Europe, where, among the Greeks, the word Psyche served not only to denote the Soul but also the Butterfly, a symbol of the Soul; and the word Mylitta served both as the name of a Goddess and of her symbol the Bee. Among the ancient Scandinavians the Bull, one of the symbols of THOR, was named a Thor, this being an example, according to Dr Alexander Wilder, " of the punning so common in those times, often making us uncertain whether the accident of similar name or sound led to adoption as a symbol or was merely a blunder." 2
I was unaware that there was any ancient warrant for what I supposed to be the novel supposition that in many / Page12 / instances the names of once-sacred animals contain within themselves the key to what was originally symbolised. The idea that identities of name were primarily due to punning, to blunder, or to accident, must be dispelled when we find that-as in most of the examples noted by myself -the symbolic value of the animal is not expressed by a homonym or pun, but in monosyllables that apparently are the debris of some marvellously ancient, prehistoric, almost extinct parent tongue. Modern language is a mosaic in which lie embedded the chips and fossils of predecessors in comparison with whose vast antiquity Sanscrit is but a speech of yesterday. In its glacier-like progress, Language must have brought down along the ages the detritus of tongues that were spoken possibly millions of years before the art of recording by writing was discovered, but which, notwithstanding, were indelibly inscribed and faithfully preserved in the form of mountain, river, and country names. Empires may disappear and nations be sunk into oblivion under successive waves of invasion, but place names and proper names, preserved traditionally by word of mouth, remain to some extent inviolate; and it is, I am convinced, in this direction that one must look for the hypothetical mother-tongue of the hypothetical people, known nowadays as "Aryans. "

Page 11. Notes.1 On the Origin and Growth of Religion as Illustrated by the Religion 0/
Ancient Egypt, p. 237 ; Hibbcrt Lectures, p. 879. 2 Symbolical Language of Ancient Art and Mythology, R. Payne-Knight,
P.124.

 

-
-
-
-
-
LANGUAGE
-
-
-
L
=
3
-
2
L
12
3
3
A
=
1
-
2
A
1
1
1
N
=
5
-
3
N
14
5
5
G
=
7
-
2
G
7
7
7
U
=
3
-
3
U
21
3
3
A
=
1
-
3
A
1
1
1
G
=
7
-
4
G
7
7
7
E
=
5
-
3
E
5
5
5
-
-
32
-
8
LANGUAGE
68
32
32
-
-
3+2
-
-
-
6+8
3+2
3+2
-
-
5
-
8
LANGUAGE
14
5
5
-
-
-
-
-
-
1+4
-
-
-
-
5
-
8
LANGUAGE
5
5
5

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
LANGUAGE
-
-
-
-
-
-
-
-
-
-
-
-
-
L
=
3
-
2
L
12
3
3
-
-
-
3
-
-
-
-
-
-
A
=
1
-
2
A
1
1
1
-
1
-
-
-
-
-
-
-
-
N
=
5
-
3
N
14
5
5
-
-
-
-
-
5
-
-
-
-
G
=
7
-
2
G
7
7
7
-
-
-
-
-
-
-
7
-
-
U
=
3
-
3
U
21
3
3
-
-
-
3
-
-
-
-
-
-
A
=
1
-
3
A
1
1
1
-
1
-
-
-
-
-
-
-
-
G
=
7
-
4
G
7
7
7
-
-
-
-
-
-
-
7
-
-
E
=
5
-
3
E
5
5
5
-
-
-
-
-
5
-
-
-
-
-
-
32
-
8
LANGUAGE
68
32
32
-
2
2
6
4
10
6
14
8
9
-
-
3+2
-
-
-
6+8
3+2
3+2
-
-
-
-
-
1+0
-
1+4
-
-
-
-
5
-
8
LANGUAGE
14
5
5
-
2
2
6
4
1
6
5
8
9
-
-
-
-
-
-
1+4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
5
-
8
LANGUAGE
5
5
5
-
2
2
6
4
1
6
5
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
3
5
7
-
-
-
-
-
LANGUAGE
-
-
-
-
-
-
-
-
L
=
3
-
2
L
12
3
3
-
-
3
-
-
A
=
1
-
2
A
1
1
1
-
1
-
-
-
N
=
5
-
3
N
14
5
5
-
-
-
5
-
G
=
7
-
2
G
7
7
7
-
-
-
-
7
U
=
3
-
3
U
21
3
3
-
-
3
-
-
A
=
1
-
3
A
1
1
1
-
1
-
-
-
G
=
7
-
4
G
7
7
7
-
-
-
-
7
E
=
5
-
3
E
5
5
5
-
-
-
5
-
-
-
32
-
8
LANGUAGE
68
32
32
-
2
6
10
14
-
-
3+2
-
-
-
6+8
3+2
3+2
-
-
-
1+0
1+4
-
-
5
-
8
LANGUAGE
14
5
5
-
2
6
1
5
-
-
-
-
-
-
1+4
-
-
-
-
-
-
-
-
-
5
-
8
LANGUAGE
5
5
5
-
2
6
1
5

 

 

-
-
-
-
-
LANGUAGE
-
-
-
L
=
3
-
2
L+A+N
27
9
9
A
=
1
-
2
G+U+A+G
18
18
9
N
=
5
-
3
E
5
5
5
-
-
32
-
8
LANGUAGE
68
32
32
-
-
3+2
-
-
-
6+8
3+2
3+2
-
-
5
-
8
LANGUAGE
14
5
5
-
-
-
-
-
-
1+4
-
-
-
-
5
-
8
LANGUAGE
5
5
5

 

 

-
-
-
-
-
LANGUAGE
-
-
-
A
=
1
-
3
A
1
1
1
A
=
1
-
2
A
1
1
1
L
=
3
-
2
L
12
3
3
U
=
3
-
3
U
21
3
3
E
=
5
-
3
E
5
5
5
N
=
5
-
3
N
14
5
5
G
=
7
-
2
G
7
7
7
G
=
7
-
4
G
7
7
7
-
-
32
-
8
LANGUAGE
68
32
32
-
-
3+2
-
-
-
6+8
3+2
3+2
-
-
5
-
8
LANGUAGE
14
5
5
-
-
-
-
-
-
1+4
-
-
-
-
5
-
8
LANGUAGE
5
5
5

 

 

SOME MYSTICAL ADVENTURES

G, R, S. Mead 1910

XIII

ON THE ART OF SYMBOLISM.

Page 180

"The Mind of the Father hath sown symbols through the world."

THE CHALDAEAN ORACLES.

" MANY people talk vaguely about symbols and some are really interested in symbolism; but even of those who may happen to possess a little learning on the subject, how few are there who, if they turn and really face themselves and there is no audience to play to, can say they have got to the heart of the matter, or know how rightly to seize the proteus whose changing forms they are ever grasping at, and so force it to speak true words?
I, for my part, freely admit that I am as yet far from the real heart of the matter. I cannot yet hold the proteus steady and force it to speak true words of power; but there is joy in the game of catch-as-can-catch, and I am game for a short bout; though doubtless, as of yore, the wily one will change into something I have never thought of before, and I shall have no grip in mind to hold him.

Page 181

'Symbol' is no native name; it is a Greek importation (symbolon), and its root-meaning is said to be a sign, or token, by which one knows or infers a thing. The utterance of this word should awaken in us the idea of putting together (sym-ballein), with the notion (in the passive) of to correspond and to tally. But to put together is to compare, and so to compare one's own opinion with facts, and hence to conclude, infer, conjecture, interpret; and it is from this last meaning that, the wisdom of the word-books tells us, we get the meaning of symbol as a sign, or token, by which one knows or infers a thing.
I am afraid that we have not yet grasped our proteus amid all these changing forms of words. A symbol is a sign, but that again is a Latin importation (signum), and we may pass it by. A symbol is a token; that is good English. Token is connected with to teach, to point out, show, witness; to betoken is to be a symbol of.
But words will not help us much; they are forms of speech that are ever slipping away into other forms. A symbol is not a word; it is something more fundamental; in its proper meaning it is something almost more primitive than an ideogram, or type-picture. Let us go in search of the idea-the living idea, not some abstract inference-the fulness, not the flat.
If there is a 'flat-land' as compared with a / Page 182 / three-dimensional land, may we not think of symbol-language as a three-dimensional language, so to speak, when compared with the' flat' languages of ordinary speech? Or, to use these words in a deeper meaning, speech in its most primitive mode is action, and so symbolic action, or drama, might be said to be the true symbol­language. This symbol - or three-dimensional language is closely connected with ceremony. And ceremony (Lat. eeremonia) is a word formed on a stem that grows from the root ere (as in creo, I make, create), which is of the same origin as the Sanskrit kri (as in karma, action, doing). A ceremony is a sacred rite; that is, it is typical, and as such should be of creative potency, for as the Chaldaean Oracle has it: "The Mind of the Father hath sown symbols through the world." That which is typical is ideal, for type and idea are synonyms.
Are we now getting any nearer the heart of the matter? Are we beginning to make our symbols alive? Can we afford to dismiss any true symbol with the dull remark: "It's only a symbol"? The universe itself is a symbol; man is a symbol.
Even in their lowest strata symbols are the ' out-lines,' so to say, of three-dimensional objects from some point of view, seen from one side or another; and' out-line' in its inner meaning is / Page 183 / intimately connected with idea; it is, as it were, a ground-plan.
Now as symbols in this sense have to do with ideas and types, are connected with the living side of things, it is not possible to interpret a symbol in one set fashion only and tie it down to one set form. We cannot make an 'exact science' of symbolism; it is initiatory rather than didactic; it 'starts' one towards living ideas, it does not peg us out in some rigid configuration.
So that if it is asked, how does one know that this or that is the right interpretation of any particular symbol, it is exceedingly difficult, if not impossible, to prove it in the way of physical demonstration. If the interpretation really fits, there will be a response within. It will be a living response; not the imprisoning of the mind in a dead form. In the interpretation of symbols we must be prepared to give up exactness, in the way it is generally understood, and allow our minds free play. At the beginning it is best to use any hint that seems to promise well; first apply it in every direction, then as soon as ever it has led to another clue, throw it away.
In learning the great language of symbols it is necessary to keep the mind ever free, plastic, and adaptable. If we persist in keeping stuck in the old ruts, we shall never learn the meaning / Page 184 / of symbols. The beauty of great symbols is the infinite variety of their modes of interpretation. To think there is only one definite interpretation for each symbol is to paralyse one's symbol-mind, and make it fall dead and flat into the superficial. One should play with symbols as a mathematician plays with numbers; symbols are the playthings of the gods. And I think the secret of interpreting symbols is to get the symbol first into one's mind, and not one's mind into the symbol.
The mind should not be allowed to relate itself to the symbol, should not allow itself to be attracted by the picture into going out of itself and crystallising itself into one form; but the symbol should rather be compelled to relate itself to the mind. It should be taken into the mind, and then the mind will be able to see it from every side and grasp it as a whole.
Symbol-language has its letters and its words, and the above may be suggested as a method of learning the alphabet. But symbol-language is not the same thing quite as symbolical language, nor is it to be confused with metaphorical language. Metaphor is transferring the meaning of one word to another in ordinary speech. It is exceedingly important, quite a mystic art, a sort of game of 'general post' among the ideas connected with words.
A metaphor gives a meaning that is not to be / Page 185 / understood literally, or according to the face­value of the letters as we know them, but a reading of root-ideas, as it were, abstracting or subtracting the substance from them. That is to say, we take away the substance that built the idea and keep the idea, and then expand it and spread it out cosmically in every direction. Metaphors may be said to be more connected with substance, symbols with spirit.
Symbols should be ' eaten' and' digested,' so to say. Triangles and svastikas, for instance, might be said to be symbols which, when gazed upon in an ecstatic state of mind-that is, taken within and contemplated-nourish the body of essence; if made alive they create pleasing sensations in it, stimulate, feed, and excite it, rearrange all its activities, alter the currents in it and build it. All great symbols are said to do this-that is, all cosmic symbols or forms that are directly related to things-that-are. These cosmic symbols suggest modes of creative energies; when creative powers act they draw certain patterns and plans and not others; and these patterns, types, and ideas are cosmic symbols, and it is by ecstatically gazing at them, that they nourish our root-substance and so enform it cosmically, or in a harmonious or orderly fashion.
Symbols are toys in the great game. We / Page 186 / should thus learn to play with symbols in the true Kindergarten, the' everlasting revelling­place '-the essential substance that is our nursery and our cradle, and our womb for birth into greater things. But this game is a living thing; we should make symbols act; we learn little while we keep them steady. A true symbol should be ever in motion. Nor should we be satisfied till we can glide from one symbol to another. While we think of symbols as dead detached objects cut off from one another, and bearing no relation to each other, we shall know nothing. We should play with them, draw them or picture them from every stand­point, till we catch fresh glimpses every moment.
Let us think of one great world-body ever in motion; all true symbols may be said to be attempts to snapshot this object in motion. They are like separate films for a cinemato­graph; the great difficulty is to get them in their right sequence and make them pass in procession before the inner eye. If we could manage to do this and obtain the right sequence for a moment, then we should get in touch with some real living ideas. But the right grouping of the symbols is essential. However, the more we practise, the better we guess, the faster will the real ideas come. It is perhaps the greatest of arts-the true practice of the / Page 187 / art of symbolism. We can do it with our minds, with our eyes, with our bodies. Indeed if we could act this continuity between symbols, we should, it is said, breathe in ideas with every movement of the essential body; but this is far more difficult than practising with our minds.
Of course all this applies only to true symbols; many things called symbols are distorted or false appearances. No signs, no symbols, are worth anything unless they signify facts; that is to say, unless they represent transformations which will be experienced when inner vision develops.
A true symbol is something capable of con­taining life. It is never of any arbitrary shape. It must be, or it will never convey living ideas. Symbols, I believe, are not given to make us think in the ordinary sense; their main use is to convey life to our life and bring about a union. Their real use is to convey life of such power that it is capable of actually making an impression, or depression, upon the substance with which the higher mind is connected. They are the link between thought and action. Symbolism is connected with sigils, signatures, characters, types, in their root-meanings, with all the nomenclature connected with the im­pression of ideas on substance.
Before a man is capable of causing his subtle / Pagee 188 / substance to go through all these transformations, * or metamorphoses, at which we have hinted, before these' initiations '-beginnings or startings-can really take place in the root­matter of his vehicles, it is possible for the transformations actually to take place in symbol in his higher mind of ideation. And this is a very desirable thing. To accomplish it in body is doubtless possible for a few only; but to accomplish it in mind is possible for many more. It is not dangerous, and it is a great developer of mental capacity.
It is a method of contemplation. The symbol­learner should strive to get the mind quite still; to get the idea of the mind being as it were a sea of subtle substance. He must not think discursively; must not space out separatE.? symbols and look at them one after the other; but try to 'feel' the mind-substance being moulded.

Page 189

If, for instance, he think of 'potter' and , clay,' he should try to imagine the substance of the mind being moulded from one to the other continuously backwards and forwards, and watch them grow within himself. When practising symbols we should never' objectivise' or project; we should rather' feel' them grow within, and then an occasional idea may flash through.
It is, however, not desirable to pay too much attention to these ideas, for noticing them immediately transfers the consciousness to another' plane' of mind; for though this practice is a mental one it is not in itself a , science.' It is better to notice the ideas that flash forth just sufficiently to record them on the memory-plate, so that they can be used later when the tranquillity of mind that is the essential condition of the practice, has been left.
The world-body, or great surround, or essence­envelope, of every man may be thought of as, so to speak, the L.C. M., or rather G.C.M., of all symbols. It is a useful practice to play with spheres and circles and conic sections, and so try to get ideas along these lines. It is quite credible that it is possible to resolve every symbol into an 'attitude,' so to say, or 'action,' or rather' activity,' of this world-body, and / Page 190 / so connect and link up all symbols by means of this world-soul, which is soul and body also.
This world-body may be said to be our way out of manhood into the cosmos; and so also is the art of symbolism the way out of men's language into the language of the gods. Root­symbols may be regarded as fundamental lines and curves which carry with them certain powers and certain meanings, and these lines and curves are to be found in every science and art of men. They are, from this standpoint, the roots from which all sciences and arts grow, the foundations on which they are built, the gates forth to greater worlds.
It is not, however, to be supposed that such symbolism is the end of the matter; by no means. It is introductory to the linking of Mind on to this world-body. Symbols are, so to say, snapshots of the self-motivity of this world-body; they teach concerning its breathing, concerning the pulsing of its heart.
And even as we can get from art to science or gnosis by means of symbols, so can we get from mind to mind and from Person to Person, - not personality, but the Higher Person or Mind.
But this world-body does not mean a mass of some vast size. This world-body has no definite size; it breathes and is a different size for every mode of breath. It is a node, rather. It is an / Page 191 / ' atom' ordered according to the greater cosmos; and in the greater cosmos the mystics say all things are the same size, or all things are any size, or, again, there is no such thing as size. It does not count in the greater consciousness, any more than we think of the' size' of our breath; though from another point of view, mystically considered, the objective worlds of size are in the breath of the Gods; they breathe and the worlds act, but the Gods do not consider their size.
It might thus be said that every man's world­body is the same size. They are all exactly alike; each is an 'atom,' each is a scale. It is our Great Person or Higher Self that decides what key the scale is in. This means that our Divine Word relates our group of 'letters,' or ' sounds,' or 'planets,' on to something further, and gives them a peculiar meaning of their own. Yet every world-body consists of the same letters, the same groups of sounds, otherwise the Holy Confraternity would be an impossibility.
All this is intimately connected with the mystery of Spirit or Divine Breath; so that when a man's mind is capable of being' fired' with Spirit, it can immediately mould and form
his substance into symbols. It is this power of continually forming man's substance into symbols which brings with it the power of understanding, / Page 192 / for symbols may be said to be the link between substance and Spirit.
It should be noted in this connection, that this language of symbols does not teach us about reincarnation; it is not on that side of things, and this interpretation cannot be forced upon it. Reincarnation is connected with the mind of man, and can be talked about in words; symbols depict the activities of Life in the man's world-body, and are not concerned with death, or form in activity, and the experiences of little persons.
Symbols have rather to do with that which is aeonian, or age-long. A true symbol must be of world-wide experience and age-long ex­perience; it must not be local or temporary.
Thus the only way to control the proteus of symbolism is by becoming him, and so keeping pace with every change, transformation, or metamorphosis; and if one is not as yet strong enough to grip the heart of the matter, at any rate it is something to know the futility of trying to get a true hold by grasping at this or that fleeting appearance.

Page 188. Notes. * The earliest redactor of the Naassene Document writes: "And the Chaldreans say that Soul is very difficult to discover and hard to understand; for it never remains of the same appearance, or form, or in the same state, so that one can describe it by a general type, or comprehend it by an essential quality." On this the Church Father Hippolytus comments, referring to the Naassenes, or Disciples of the Serpent of Wisdom: "These variegated metamorphoses they have laid down in the Gospel super­scribed 'According to the Egyptians.''' (See Thrice­greatest Hermes, i. 150.)

 

NAASSENE 51111555 NAASSENE

 

-
-
-
-
-
NAASSENE
-
-
-
N
=
5
-
1
N
14
5
5
A
=
1
-
1
A
1
1
1
A
=
1
-
1
A
1
1
1
S
=
1
-
1
S
19
10
1
S
=
1
-
1
S
19
10
1
E
=
5
-
1
E
5
5
5
N
=
5
-
1
N
14
5
5
E
=
5
-
1
E
5
5
5
-
-
24
-
8
NAASSENE
78
42
24
-
-
2+4
-
-
-
7+8
4+2
2+4
-
-
6
4
8
NAASSENE
15
6
6
-
-
-
-
-
-
1+5
-
-
-
-
6
4
8
NAASSENE
6
6
6

 

 

-
-
-
-
-
NAASSENES
-
-
-
N
=
5
-
1
N
14
5
5
A
=
1
-
1
A
1
1
1
A
=
1
-
1
A
1
1
1
S
=
1
-
1
S
19
10
1
S
=
1
-
1
S
19
10
1
E
=
5
-
1
E
5
5
5
N
=
5
-
1
N
14
5
5
E
=
5
-
1
E
5
5
5
S
=
1
-
1
S
19
10
1
-
-
25
-
9
NAASSENES
97
52
25
-
-
2+5
-
-
-
9+7
5+2
2+5
-
-
7
4
9
NAASSENES
16
7
7
-
-
-
-
-
-
1+6
-
-
-
-
7
4
9
NAASSENES
7
7
7

 

 

-
-
-
-
-
NAASSENES
-
-
-
N
=
5
-
1
N
14
5
5
A
=
1
-
1
A+A+S+S+S
59
32
5
E
=
5
-
1
E
5
5
5
N
=
5
-
1
N
14
5
5
E
=
5
-
1
E
5
5
5
-
-
25
-
9
NAASSENES
97
52
25
-
-
2+5
-
-
-
9+7
5+2
2+5
-
-
7
4
9
NAASSENES
16
7
7
-
-
-
-
-
-
1+6
-
-
-
-
7
4
9
NAASSENES
7
7
7

 

 

LIGHT 56-29-11-2-11-29-56 LIGHT

ISIS 56-20-2-2-56 ISIS

 

 

THE

LOST LANGUAGE OF SYMBOLISM

AN ENQUIRY INTO THE ORIGIN OF CERTAIN

LETTERS, WORDS, NAMES, FAIRY-TALES, FOLK-LORE AND MYTHOLOGIES

Harold Bayley 1912

"The Hebrew for man is ish and for woman isha."

Page 300

"Each language, whether Sanscrit or Zulu, is like a palimpsest, which, if carefully handled, will disclose the original text beneath the superficial writing, and though that original text may be more difficult to recover in illiterate languages, yet it is there nevertheless. Every language, if properly summoned, will reveal to us the mind of the artist who framed it, from its earliest awakening to its latest dreams. Everyone will teach us the same lesson, the lesson on which the whole Science of Thought is based, that there is no language without reason, as there is no reason with.out language."1 An analysis of the several terms for man, soul, or spirit reveals the time-honoured belief that the human race emerged in its infancy from the Great Light, and that every human soul was a spark or fragment of the Ever­Existent Oversoul. The Egyptian for man was se, the German for soul is seele - cognate with Selah! - and meaning likewise the "Light of the Everlasting." The Dutch for soul is ziel, the fiery light of God, and the English soul was once presumably is ol, the essence or light of God.2 The Hebrew for man is ish and for woman isha.

 

SELAH HALES

 

 

THE

LOST LANGUAGE OF SYMBOLISM

Harold Bayley 1912

Page 300

The Latin homo is OM, the Sun, as also is the French homme ; and dme, the French for soul, is apparently the Hindoo AUM. The ancient Mexicans traced their descent from an ancestor named Coxcox, i.e. ack ock se, ack ock se, the "Great Great Light, the Great Great Light." 8 The Teutons claim to have descended from TIU or TUISCO, an Aryan God of Light, and the name TUISCO may be restored into tu is ack O , the "brilliant light of the Great O."

Page 300 Notes

1 Biographieses of Words, Intro.
2 We may see similar vowel erosion going on at the present day, and the word cute will soon take its place in the dictionaries in addition to acute, its proper form.
3 This doubling of a title is a world-wide commonplace, similar to our " King of Kings and Lord of Lords, Very God of Very God."

 

 

THE MAGIC MOUNTAIN

Thomas Mann 1875-1955

Page 466

"Had not the normal, since time was, lived on the achievements of the abnormal? Men consciously and voluntarily descended into disease and madness, in search of knowledge which, acquired by fanaticism, would lead back to health; after the possession and use of it had ceased to be conditioned by that heroic and abnormal act of sacrifice. That was the true death on the cross, the true Atonement." "

 

THE TRUE DEATH ON THE CROSS THE TRUE AT ONE MENT

 

 

ATONEMENT

 

-
-
-
-
A
-
-
-
-
-
-
-
-
T
-
-
-
-
-
-
-
-
O
-
-
-
-
-
-
-
-
N
-
-
-
-
A
T
O
N
E
M
E
N
T
-
-
-
-
M
-
-
-
-
-
-
-
-
E
-
-
-
-
-
-
-
-
N
-
-
-
-
-
-
-
-
T
-
-
-
-

 

 

CRUCIFIXION

 

-
-
-
-
-
C
-
-
-
-
-
-
-
-
-
-
R
-
-
-
-
-
-
-
-
-
-
U
-
-
-
-
-
-
-
-
-
-
C
-
-
-
-
-
-
-
-
-
-
I
-
-
-
-
-
C
R
U
C
I
F
I
X
I
O
N
-
-
-
-
-
I
-
-
-
-
-
-
-
-
-
-
X
-
-
-
-
-
-
-
-
-
-
I
-
-
-
-
-
-
-
-
-
-
O
-
-
-
-
-
-
-
-
-
-
N
-
-
-
-
-

 

 

CRUCIFIED

 

-
-
-
-
C
-
-
-
-
-
-
-
-
R
-
-
-
-
-
-
-
-
U
-
-
-
-
-
-
-
-
C
-
-
-
-
C
R
U
C
I
F
I
E
D
-
-
-
-
F
-
-
-
-
-
-
-
-
I
-
-
-
-
-
-
-
-
E
-
-
-
-
-
-
-
-
D
-
-
-
-

 

 

HOLY BIBLE
Scofield References
Page 1117 A.D. 30.
Jesus answered and said unto him, Verily, verily,
I say unto thee, Except a man be born again,
He cannot see the kingdom of God.
St John Chapter 3 verse 3
3 + 3 3 x 3
6 x 9
54
5 + 4
9

 

 

IN SEARCH OF THE MIRACULOUS

Fragments of an Unknown Teaching

P.D.Oupensky 1878-1947

Page 217

'A man may be born, but in order to be born he must first die, and in order to die he must first awake.'
" 'When a man awakes he can die; when he dies he can be born' "

 

 

THIS IS THE SCENE OF THE SCENE UNSEEN

THE UNSEEN SEEN OF THE SCENE UNSEEN THIS IS THE SCENE

 

 

3
THE
33
15
6
4
MIND
40
22
4
2
OF
21
12
3
9
HUMANKIND
95
41
5
18
First Total
189
90
18
1+8
Add to Reduce
1+8+9
9+0
1+8
9
Second Total
18
9
9
-
Reduce to Deduce
1+8
-
-
9
Essence of Number
9
9
9

 

 

THE

FAR YONDER SCRIBE

AND OFT TIMES SHADOWED SUBSTANCES WATCHED IN FINE AMAZE

THE

ZED ALIZ ZED

IN

SWIFT REPEAT SCATTER STAR DUST AMONGST THE LETTERS OF THEIR PROGRESS

 

 

NUMBER

9

THE SEARCH FOR THE SIGMA CODE

Cecil Balmond 1998

Cycles and Patterns

Page 165

Patterns

"The essence of mathematics is to look for patterns.

Our minds seem to be organised to search for relationships and sequences. We look for hidden orders.

These intuitions seem to be more important than the facts themselves, for there is always the thrill at finding something, a pattern, it is a discovery - what was unknown is now revealed. Imagine looking up at the stars and finding the zodiac!

Searching out patterns is a pure delight.

Suddenly the counters fall into place and a connection is found, not necessarily a geometric one, but a relationship between numbers, pictures of the mind, that were not obvious before. There is that excitement of finding order in something that was otherwise hidden.

And there is the knowledge that a huge unseen world lurks behind the facades we see of the numbers themselves."

 

 

FINGERPRINTS OF THE GODS

A QUEST FOR THE BEGINNING AND THE END

Graham Hancock 1995

Chapter 32

Speaking to the Unborn

Page 285

"It is understandable that a huge range of myths from all over the ancient world should describe geological catastrophes in graphic detail. Mankind survived the horror of the last Ice Age, and the most plausible source for our enduring traditions of flooding and freezing, massive volcanism and devastating earthquakes is in the tumultuous upheavals unleashed during the great meltdown of 15,000 to 8000 BC. The final retreat of the ice sheets, and the consequent 300-400 foot rise in global sea levels, took place only a few thousand years before the beginning of the historical period. It is therefore not surprising that all our early civilizations should have retained vivid memories of the vast cataclysms that had terrified their forefathers.
Much harder to explain is the peculiar but distinctive way the myths of cataclysm seem to bear the intelligent imprint of a guiding hand.l Indeed the degree of convergence between such ancient stories is frequently remarkable enough to raise the suspicion that they must all have been 'written' by the same 'author'.
Could that author have had anything to do with the wondrous deity, or superhuman, spoken of in so many of the myths we have reviewed, who appears immediately after the world has been shattered by a horrifying geological catastrophe and brings comfort and the gifts of civilization to the shocked and demoralized survivors?
White and bearded, Osiris is the Egyptian manifestation of this / Page 286 / universal figure, and it may not be an accident that one of the first acts he is remembered for in myth is the abolition of cannibalism among the primitive inhabitants of the Nile Valley.2 Viracocha, in South America, was said to have begun his civilizing mission immediately after a great flood; Quetzalcoatl, the discoverer of maize, brought the benefits of crops, mathematics, astronomy and a refined culture to Mexico after the Fourth Sun had been overwhelmed by a destroying deluge.
Could these strange myths contain a record of encounters between scattered palaeolithic tribes which survived the last Ice Age and an as yet unidentified high civilization which passed through the same epoch?
And could the myths be attempts to communicate?

A message in the bottle of time"

'Of all the other stupendous inventions,' Galileo once remarked,

what sublimity of mind must have been his who conceived how to communicate his most secret thoughts to any other person, though very distant either in time or place, speaking with those who are in the Indies, speaking to those who are not yet born, nor shall be this thousand or ten thousand years? And with no greater difficulty than the various arrangements of two dozen little signs on paper? Let this be the seal of all the admirable inventions of men.3

If the 'precessional message' identified by scholars like Santillana, von Dechend and Jane Sellers is indeed a deliberate attempt at communication by some lost civilization of antiquity, how come it wasn't just written down and left for us to find? Wouldn't that have been easier than encoding it in myths? Perhaps.
Nevertheless, suppose that whatever the message was written on got destroyed or worn away after many thousands of years? Or suppose that the language in which it was inscribed was later forgotten utterly (like the enigmatic Indus Valley script, which has been studied closely for more than half a century but has so far resisted all attempts at decoding)? It must be obvious that in such circumstances a written / Page 287 / legacy to the future would be of no value at all, because nobody would be able to make sense of it.
What one would look for, therefore, would be a universal language, the kind of language that would be comprehensible to any technologically advanced society in any epoch, even a thousand or ten thousand years into the future. Such languages are few and far between, but mathematics is one of them - and the city of Teotihuacan may be the calling-card of a lost civilization written in the eternal language of mathematics.
Geodetic data, related to the exact positioning of fixed geographical points and to the shape and size of the earth, would also remain valid and recognizable for tens of thousands of years, and might be most conveniently expressed by means of cartography (or in the construction of giant geodetic monuments like the Great Pyramid of Egypt, as we shall see).
Another 'constant' in our solar system is the language of time: the great but regular intervals of time calibrated by the inch-worm creep of precessional motion. Now, or ten thousand years in the future, a message that prints out numbers like 72 or 2160 or 4320 or 25,920 should be instantly intelligible to any civilization that has evolved a modest talent for mathematics and the ability to detect and measure the almost imperceptible reverse wobble that the sun appears to make along the ecliptic against the background of the fixed stars..."

"What one would look for, therefore, would be a universal language, the kind of language that would be comprehensible to any technologically advanced society in any epoch, even a thousand or ten thousand years into the future. Such languages are few and far between, but mathematics is one of them"

"WRITTEN IN THE ETERNAL LANGUAGE OF MATHEMATICS"

 

 

-
ALL IS NUMBER
-
-
-
3
ALL
25
7
7
2
IS
28
10
1
6
NUMBER
73
28
1
11
ALL IS NUMBER
126
45
9
1+1
-
1+2+6
4+5
-
2
ALL IS NUMBER
9
9
9

 

 

-
17
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
-
5
9
-
-
-
1
-
-
-
-
-
5
-
-
-
-
-
+
=
20
2+0
=
2
=
2
=
2
-
-
-
14
9
-
-
-
19
-
-
-
-
-
14
-
-
-
-
-
+
=
56
5+6
=
11
1+1
2
=
2
-
17
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
3
-
-
4
5
9
-
1
3
-
3
1
-
7
3
1
7
5
+
=
52
5+2
=
7
=
7
=
7
-
-
21
-
-
22
5
18
-
1
12
-
12
1
-
7
21
1
7
5
+
=
133
1+3+3
=
7
=
7
=
7
-
17
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
21
14
9
22
5
18
19
1
12
-
12
1
14
7
21
1
7
5
+
=
189
1+8+9
=
18
1+8
9
=
9
-
-
3
5
9
4
5
9
1
1
3
-
3
1
5
7
3
1
7
5
+
=
72
7+2
=
9
=
9
=
9
-
17
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
-
-`
-
-
-
-
1
1
-
-
-`
1
-
-
-
1
-
-
-
-
1
occurs
x
4
=
4
=
4
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
2
TWO
-
-
-
-
-
-
-
-
3
-
-
-
-
-
-
-
3
-
3
-
-
-
3
-
-
-
-
-
3
occurs
x
4
=
12
1+2
3
-
-
-
-
-
4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
4
occurs
x
1
=
4
=
4
-
-
-
5
-
-
5
-
-
-
-
-
-
-
5
-
-
-
-
5
-
-
5
occurs
x
4
=
20
2+0
2
6
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
6
SIX
6
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
7
-
-
7
-
-
-
7
occurs
x
2
=
14
1+4
5
8
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
8
EIGHT
8
-
-
-
-
-
-
-
-
-
9
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
occurs
x
2
=
18
1+8
9
16
17
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
29
-
-
17
-
72
-
27
1+6
1+7
-
-
9
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
2+9
-
-
1+7
-
7+2
-
2+7
7
8
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
11
-
-
8
-
9
-
9
-
-
3
5
9
4
5
9
1
1
3
-
3
1
5
7
3
1
7
5
-
-
1+1
-
-
-
-
-
-
-
7
8
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
2
-
-
8
-
9
-
9

 

 

17
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
5
9
-
-
-
1
-
-
-
-
-
5
-
-
-
-
-
+
=
20
2+0
=
2
=
2
=
2
-
-
14
9
-
-
-
19
-
-
-
-
-
14
-
-
-
-
-
+
=
56
5+6
=
11
1+1
2
=
2
17
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
3
-
-
4
5
9
-
1
3
-
3
1
-
7
3
1
7
5
+
=
52
5+2
=
7
=
7
=
7
-
21
-
-
22
5
18
-
1
12
-
12
1
-
7
21
1
7
5
+
=
133
1+3+3
=
7
=
7
=
7
17
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
21
14
9
22
5
18
19
1
12
-
12
1
14
7
21
1
7
5
+
=
189
1+8+9
=
18
1+8
9
=
9
-
3
5
9
4
5
9
1
1
3
-
3
1
5
7
3
1
7
5
+
=
72
7+2
=
9
=
9
=
9
17
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
-`
-
-
-
-
1
1
-
-
-`
1
-
-
-
1
-
-
-
-
1
occurs
x
4
=
4
=
4
-
3
-
-
-
-
-
-
-
3
-
3
-
-
-
3
-
-
-
-
-
3
occurs
x
4
=
12
1+2
3
-
-
-
-
4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
4
occurs
x
1
=
4
=
4
-
-
5
-
-
5
-
-
-
-
-
-
-
5
-
-
-
-
5
-
-
5
occurs
x
4
=
20
2+0
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
7
-
-
7
-
-
-
7
occurs
x
2
=
14
1+4
5
-
-
-
9
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
occurs
x
2
=
18
1+8
9
17
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
29
-
-
17
-
72
-
27
1+7
-
-
9
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
2+9
-
-
1+7
-
7+2
-
2+7
8
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
11
-
-
8
-
9
-
9
-
3
5
9
4
5
9
1
1
3
-
3
1
5
7
3
1
7
5
-
-
1+1
-
-
-
-
-
-
-
8
U
N
I
V
E
R
S
A
L
-
L
A
N
G
U
A
G
E
-
-
2
-
-
8
-
9
-
9

 

 

-
11
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
1
-
5
-
-
-
-
-
+
=
15
1+5
=
6
=
6
=
6
-
-
-
-
-
-
9
19
-
14
-
-
-
-
-
+
=
42
4+2
=
6
=
6
=
6
-
11
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
-
-
-
-
-
-
-
-
-
-
1
3
3
-
-
-
-
-
3
4
2
5
9
+
=
30
3+0
=
3
=
3
=
3
-
-
1
12
12
-
-
-
-
-
21
13
2
5
18
+
=
84
8+4
=
12
1+2
3
=
3
-
11
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
-
-
-
-
-
-
-
-
-
-
1
12
12
-
9
19
-
14
21
13
2
5
18
+
=
126
1+2+6
=
9
=
9
=
9
-
-
1
3
3
-
9
1
-
5
3
4
2
5
9
+
=
45
4+5
=
9
=
9
=
9
-
11
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
1
-
-
-
-
-
-
-
-
-
1
occurs
x
2
=
2
=
2
-
-
-
-
-
-
-
-
-
-
-
-
2
-
-
-
-
2
occurs
x
1
=
2
=
2
-
-
-
3
3
-
-
-
-
-`
3
-
-
-
-
-
-
3
occurs
x
3
=
9
=
9
-
-
-
-
-
-
-
-
-
-
-
4
-
-
-
-
-
4
occurs
x
1
=
4
=
4
-
-
-
-
-
-
-
-
-
5
-
-
-
5
-
-
-
5
occurs
x
2
=
10
1+0
1
6
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
6
SIX
6
-
-
-
-
-
7
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
7
SEVEN
7
-
-
-
-
-
8
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
8
EIGHT
8
-
-
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
9
-
-
9
occurs
x
2
=
18
1+8
9
21
11
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
24
-
-
11
-
45
-
27
2+1
1+1
-
-
-
-
9
-
-
-
-
-
-
-
9
-
-
2+4
-
-
1+1
-
4+5
-
2+7
3
2
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
6
-
-
2
-
9
-
9

 

 

11
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
1
-
5
-
-
-
-
-
+
=
15
1+5
=
6
=
6
=
6
-
-
-
-
-
9
19
-
14
-
-
-
-
-
+
=
42
4+2
=
6
=
6
=
6
11
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
-
-
-
-
-
-
-
-
-
1
3
3
-
-
-
-
-
3
4
2
5
9
+
=
30
3+0
=
3
=
3
=
3
-
1
12
12
-
-
-
-
-
21
13
2
5
18
+
=
84
8+4
=
12
1+2
3
=
3
11
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
-
-
-
-
-
-
-
-
-
1
12
12
-
9
19
-
14
21
13
2
5
18
+
=
126
1+2+6
=
9
=
9
=
9
-
1
3
3
-
9
1
-
5
3
4
2
5
9
+
=
45
4+5
=
9
=
9
=
9
11
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
1
-
-
-
-
-
-
-
-
-
1
occurs
x
2
=
2
=
2
-
-
-
-
-
-
-
-
-
-
-
2
-
-
-
-
2
occurs
x
1
=
2
=
2
-
-
3
3
-
-
-
-
-`
3
-
-
-
-
-
-
3
occurs
x
3
=
9
=
9
-
-
-
-
-
-
-
-
-
-
4
-
-
-
-
-
4
occurs
x
1
=
4
=
4
-
-
-
-
-
-
-
-
5
-
-
-
5
-
-
-
5
occurs
x
2
=
10
1+0
1
-
-
-
-
-
9
-
-
-
-
-
-
-
9
-
-
9
occurs
x
2
=
18
1+8
9
11
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
24
-
-
11
-
45
-
27
1+1
-
-
-
-
9
-
-
-
-
-
-
-
9
-
-
2+4
-
-
1+1
-
4+5
-
2+7
2
A
L
L
-
I
S
-
N
U
M
B
E
R
-
-
6
-
-
2
-
9
-
9

 

 

-
ALL IS NUMBER
-
-
-
3
ALL
25
7
7
2
IS
28
10
1
6
NUMBER
73
28
1
11
ALL IS NUMBER
126
45
9
1+1
-
1+2+6
4+5
-
2
ALL IS NUMBER
9
9
9

 

 

-
THE RAINBOW LIGHT
-
-
-
3
THE
33
15
6
7
RAINBOW
82
37
1
5
LIGHT
56
29
2
15
THE RAINBOW LIGHT
171
81
9
1+5
-
1+7+1
8+1
-
6
THE RAINBOW LIGHT
9
9
9

 

 

15
THE RAINBOW LIGHT
-
-
-
-
THE
33
15
6
-
R
18
9
9
-
A
1
1
1
-
I
9
9
9
-
N+B+O+W
54
18
9
-
L
12
3
3
-
I
9
9
9
-
G+H+T
35
17
8
15
THE RAINBOW LIGHT
171
81
54
1+5
-
1+7+1
8+1
5+4
6
THE RAINBOW LIGHT
9
9
9

 

 

THE LIGHT IS RISING NOW RISING IS THE LIGHT

 

 

26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
8
9
-
-
-
-
5
6
-
-
-
1
-
-
-
-
6
-
8
+
=
43
4+3
=
7
=
7
=
7
-
-
-
-
-
-
-
-
8
9
-
-
-
-
14
15
-
-
-
19
-
-
-
-
24
-
26
+
=
115
1+1+5
=
7
=
7
=
7
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
-
-
1
2
3
4
-
-
7
8
9
-
2
3
4
5
-
7
-
+
=
83
8+3
=
11
1+1
2
=
2
-
1
2
3
4
5
6
7
-
-
10
11
12
13
-
-
16
17
18
-
20
21
22
23
-
25
-
+
=
236
2+3+6
=
11
1+1
2
=
2
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
+
=
351
3+5+1
=
9
=
9
=
9
-
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
+
=
126
1+2+6
=
9
=
9
=
9
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
+
=
1
occurs
x
3
=
3
=
3
-
-
2
-
-
-
-
-
-
-
-
2
-
-
-
-
-
-
-
-
2
-
-
-
-
-
-
+
=
2
occurs
x
3
=
6
=
6
-
-
-
3
-
-
-
-
-
-
-
-
3
-
-
-
-
-
-
-
-
3
-
-
-
-
-
+
=
3
occurs
x
3
=
9
=
9
-
-
-
-
4
-
-
-
-
-
-
-
-
4
-
-
-
-
-
-
-
-
4
-
-
-
-
+
=
4
occurs
x
3
=
12
1+2
3
-
-
-
-
-
5
-
-
-
-
-
-
-
-
5
-
-
-
-
-
-
-
-
5
-
-
-
+
=
5
occurs
x
3
=
15
1+5
6
-
-
-
-
-
-
6
-
-
-
-
-
-
-
-
6
-
-
-
-
-
-
-
-
6
-
-
+
=
6
occurs
x
3
=
18
1+8
9
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
-
7
-
+
=
7
occurs
x
3
=
21
2+1
3
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
8
+
=
8
occurs
x
3
=
24
2+4
6
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
+
=
9
occurs
x
2
=
18
1+8
9
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
45
-
-
26
-
126
-
54
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
4+5
-
-
2+6
-
1+2+6
-
5+4
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
9
-
-
8
-
9
-
9
-
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
-
-
-
-
-
-
-
-
-
-
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
9
-
-
8
-
9
-
9

 

 

A
-
J
-
S
-
-
-
-
-
--
1
-
1
-
1
+
=
3
-
=
3
A
-
J
-
S
-
-
-
-
-
--
-
-
-
-
-
-
-
-
-
-
-
B
-
K
-
T
-
-
-
-
-
--
2
-
2
-
2
+
=
6
-
=
6
B
-
K
-
T
-
-
-
-
-
--
-
-
-
-
-
-
-
-
-
-
-
C
-
L
-
U
-
-
-
-
-
--
3
-
3
-
3
+
=
9
-
=
9
C
-
L
-
U
-
-
-
-
-
--
-
-
-
-
-
-
-
-
-
-
-
D
-
M
-
V
-
-
-
-
-
--
4
-
4
-
4
+
=
12
1+2
=
3
D
-
M
-
V
-
-
-
-
-
--
-
-
-
-
-
-
-
-
-
-
-
E
-
N
-
W
-
-
-
-
-
--
5
-
5
-
5
+
=
15
1+5
=
6
E
-
N
-
W
-
-
-
-
-
--
-
-
-
-
-
-
-
-
-
-
-
F
-
O
-
X
-
-
-
-
-
--
6
-
6
-
6
+
=
18
1+8
=
9
F
-
O
-
X
-
-
-
-
-
--
-
-
-
-
-
-
-
-
-
-
-
G
-
P
-
Y
-
-
-
-
-
--
7
-
7
-
7
+
=
21
2+1
=
3
G
-
P
-
Y
-
-
-
-
-
--
-
-
-
-
-
-
-
-
-
-
-
H
-
Q
-
Z
-
-
-
-
-
--
8
-
8
-
8
+
=
24
2+4
=
6
H
-
Q
-
Z
-
-
-
-
-
--
-
-
-
-
-
-
-
-
-
-
-
I
-
R
-
-
-
-
-
-
-
--
9
-
9
-
-
+
=
18
1+8
=
9
I
-
R
-
-
-
-
-
-
-
--
-
-
-
-
-
-
-
126
-
-
54
-
-
-
-
-
-
-
1+2+6
-
-
5+4
-
-
-
-
-
-
-
9
-
-
9

 

 

3
3
-
-
A+B+C
6
6
6
2
-
-
2
D+E
9
9
9
3
3
-
-
F+G+H
21
21
3
1
-
-
1
I
9
9
9
3
3
-
-
J+K+L
33
6
6
2
-
-
2
M+N
27
9
9
2
2
-
-
O+P
31
13
4
3
-
-
3
Q+R+S
54
18
9
3
-
-
3
T+U+V
63
9
9
3
-
-
3
W+X+Y
72
18
9
1
1
-
-
Z
26
8
8
26
12
4
14
Add to Reduce
351
126
81
2+6
1+2
-
1+4
Reduce to Deduce
3+5+1
1+2+6
8+1
8
3
-
5
Essence of Number
9
9
9

 

 

3
A+B+C
6
6
6
-
D+E
-
-
-
3
F+G+H
21
21
3
-
I
-
-
-
3
J+K+L
33
6
6
-
M+N
-
-
-
2
O+P
31
13
4
-
Q+R+S
-
-
-
-
T+U+V
-
-
-
-
W+X+Y
-
-
-
1
Z
26
8
8
12
Add to Reduce
117
54
27
2+6
Reduce to Deduce
1+1+7
5+4
2+7
8
Essence of Number
9
9
9

 

 

-
A+B+C
-
-
-
2
D+E
9
9
9
-
F+G+H
-
-
-
1
I
9
9
9
-
J+K+L
-
-
-
2
M+N
27
9
9
-
O+P
-
-
-
3
Q+R+S
54
18
9
3
T+U+V
63
9
9
3
W+X+Y
72
18
9
-
Z
-
-
-
14
Add to Reduce
234
72
54
1+4
Reduce to Deduce
2+3+4
7+2
5+4
5
Essence of Number
9
9
9

 

 

8
LANGUAGE
68
32
5
3
AND
19
10
1
6
NUMBER
73
28
1

 

 

8
LANGUAGE
68
32
5
3
AND
19
10
1
6
NUMBER
73
28
1

 

 

8
LANGUAGE
68
32
5
3
AND
19
10
1
6
NUMBER
73
28
1

 

 

7
NUMBERS
92
29
2
3
AND
19
10
1
9
LANGUAGES
87
33
6
19
First Total
198
72
9
1+9
Add to Reduce
1+9+8
7+2
-
10
Second Total
18
9
9
1+0
Reduce to Deduce
1+8
-
-
1
Essence of Number
9
9
9

 

 

9
TWENTY SIX
159
42
6
7
LETTERS
99
27
9
2
IN
23
14
5
3
THE
33
15
6
8
ALPHABET
65
29
2
29
First Total
379
127
28
2+9
Add to Reduce
3+7+9
1+2+7
2+8
11
Second Total
19
10
10
1+1
Reduce to Deduce
1+9
1+0
1+0
2
Third Total
10
1
1
-
Add to Reduce
1+0
-
-
2
Essence of Number
1
1
1

 

THE LIGHT IS RISING NOW RISING IS THE LIGHT

 

 

0
-
Z
=
8
1
4
ZERO
64
28
1
1
-
O
=
6
2
3
ONE
34
16
7
2
-
T
=
2
3
3
TWO
58
13
4
3
-
T
=
2
4
5
THREE
56
29
2
4
-
F
=
6
5
4
FOUR
60
24
6
5
-
F
=
6
6
4
FIVE
42
24
6
6
-
S
=
1
7
3
SIX
52
16
7
7
-
S
=
1
8
5
SEVEN
65
20
2
8
-
E
=
5
9
5
EIGHT
49
31
4
9
-
N
=
5
10
4
NINE
42
24
6
45
-
-
-
42
-
40
Add
522
225
45
4+5
-
-
-
4+2
-
4+0
Reduce
5+2+2
2+2+5
4+5
9
-
-
-
6
-
4
Deduce
9
9
9

 

 

-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
0
-
Z
=
8
1
4
ZERO
64
28
1
-
1
-
-
-
-
-
-
-
-
1
-
O
=
6
2
3
ONE
34
16
7
-
-
-
-
-
-
-
7
-
-
2
-
T
=
2
3
3
TWO
58
13
4
-
-
-
-
4
-
-
-
-
-
3
-
T
=
2
4
5
THREE
56
29
2
-
-
2
-
-
-
-
-
-
-
4
-
F
=
6
5
4
FOUR
60
24
6
-
-
-
-
-
-
6
-
-
-
5
-
F
=
6
6
4
FIVE
42
24
6
-
-
-
-
-
-
6
-
-
-
6
-
S
=
1
7
3
SIX
52
16
7
-
-
-
-
-
-
-
7
-
-
7
-
S
=
1
8
5
SEVEN
65
20
2
-
-
2
-
-
-
-
-
-
-
8
-
E
=
5
9
5
EIGHT
49
31
4
-
-
-
-
4
-
-
-
-
-
9
-
N
=
5
10
4
NINE
42
24
6
-
-
-
-
-
-
6
-
-
-
45
-
-
-
42
-
40
Add
522
225
45
-
1
4
3
8
5
18
14
8
9
4+5
-
-
-
4+2
-
4+0
Reduce
5+2+2
2+2+5
4+5
-
-
-
-
-
-
1+8
1+4
-
-
9
-
-
-
6
-
4
Deduce
9
9
9
-
1
4
3
8
5
9
5
8
9

 

 

1
-
O
=
6
-
3
ONE
34
16
7
2
-
T
=
2
-
3
TWO
58
13
4
3
-
T
=
2
-
5
THREE
56
29
2
4
-
F
=
6
-
4
FOUR
60
24
6
5
-
F
=
6
-
4
FIVE
42
24
6
6
-
S
=
1
-
3
SIX
52
16
7
7
-
S
=
1
-
5
SEVEN
65
20
2
8
-
E
=
5
-
5
EIGHT
49
31
4
9
-
N
=
5
-
4
NINE
42
24
6
45
-
-
-
34
-
36
Add
458
197
44
4+5
-
-
-
3+4
-
3+6
Reduce
4+5+8
1+9+7
4+4
9
-
-
-
7
4
9
Deduce
17
17
8
-
-
-
-
-
-
-
Produce
1+7
1+7
-
9
-
-
-
7
-
9
Essence
8
8
8

 

 

-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
O
=
6
1
3
ONE
34
16
7
-
-
-
-
-
-
-
7
-
-
2
-
T
=
2
2
3
TWO
58
13
4
-
-
-
-
4
-
-
-
-
-
3
-
T
=
2
3
5
THREE
56
29
2
-
-
2
-
-
-
-
-
-
-
4
-
F
=
6
4
4
FOUR
60
24
6
-
-
-
-
-
-
6
-
-
-
5
-
F
=
6
5
4
FIVE
42
24
6
-
-
-
-
-
-
6
-
-
-
6
-
S
=
1
6
3
SIX
52
16
7
-
-
-
-
-
-
-
7
-
-
7
-
S
=
1
7
5
SEVEN
65
20
2
-
-
2
-
-
-
-
-
-
-
8
-
E
=
5
8
5
EIGHT
49
31
4
-
-
-
-
4
-
-
-
-
-
9
-
N
=
5
9
4
NINE
42
24
6
-
-
-
-
-
-
6
-
-
-
45
-
-
-
34
-
36
Add
458
197
44
-
1
4
3
8
5
18
14
8
9
4+5
-
-
-
3+4
4
3+6
Reduce
4+5+8
1+9+7
4+4
-
-
-
-
-
-
1+8
1+4
-
-
9
-
-
-
7
4
9
Deduce
17
17
8
-
1
4
3
8
5
18
14
8
9
-
-
-
-
-
-
-
Produce
1+7
1+7
-
-
-
-
-
-
-
-
-
-
-
9
-
-
-
7
-
9
Essence
8
8
8
-
1
4
3
8
5
9
5
8
9

 

 

0
-
4
ZERO
8
5
9
6
-
=
28
2+8
=
10
1+0
1
1
-
3
ONE
6
5
5
-
-
=
16
1+6
=
7
-
7
2
-
3
TWO
2
5
6
-
-
=
13
1+3
=
4
-
4
3
-
5
THREE
2
8
9
5
5
=
29
2+9
=
11
1+1
2
4
-
4
FOUR
6
6
3
9
-
=
24
2+4
=
6
-
6
5
-
4
FIVE
6
9
4
5
-
=
24
2+4
=
6
-
6
6
-
3
SIX
1
9
6
-
-
=
16
1+6
=
7
-
7
7
-
5
SEVEN
1
5
4
5
5
=
20
2+0
=
2
-
2
8
-
5
EIGHT
5
9
7
8
2
=
31
3+1
=
4
-
4
9
-
4
NINE
5
9
5
5
-
=
24
2+4
=
6
-
6
45
-
40
Add
42
70
58
43
12
-
225
-
-
63
-
45
4+5
-
4+0
-
4+2
7+0
5+8
4+3
1+2
-
2+2+5
-
-
6+3
-
4+5
9
-
4
Reduce
6
7
13
7
3
-
9
-
-
9
-
-
-
-
-
-
-
-
1+3
-
-
-
-
-
-
-
-
-
9
-
4
Deduce
6
7
4
7
3
-
9
-
-
9
-
9

 

 

-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
0
-
Z
=
8
1
4
ZERO
64
28
1
-
1
-
-
-
-
-
-
-
-
1
-
O
=
6
2
3
ONE
34
16
7
-
-
-
-
-
-
-
7
-
-
2
-
T
=
2
3
3
TWO
58
13
4
-
-
-
-
4
-
-
-
-
-
3
-
T
=
2
4
5
THREE
56
29
2
-
-
2
-
-
-
-
-
-
-
4
-
F
=
6
5
4
FOUR
60
24
6
-
-
-
-
-
-
6
-
-
-
5
-
F
=
6
6
4
FIVE
42
24
6
-
-
-
-
-
-
6
-
-
-
6
-
S
=
1
7
3
SIX
52
16
7
-
-
-
-
-
-
-
7
-
-
7
-
S
=
1
8
5
SEVEN
65
20
2
-
-
2
-
-
-
-
-
-
-
8
-
E
=
5
9
5
EIGHT
49
31
4
-
-
-
-
4
-
-
-
-
-
9
-
N
=
5
10
4
NINE
42
24
6
-
-
-
-
-
-
6
-
-
-
45
-
-
-
42
-
40
Add
522
225
45
-
1
4
3
8
5
18
14
8
9
4+5
-
-
-
4+2
-
4+0
Reduce
5+2+2
2+2+5
4+5
-
-
-
-
-
-
1+8
1+4
-
-
9
-
-
-
6
-
4
Deduce
9
9
9
-
1
4
3
8
5
9
5
8
9

 

ZERO ONE TWO THREE FOUR FIVE SIX SEVEN EIGHT NINE

ZEROONETWOTHREEFOURFIVESIXSEVENEIGHTNINE

ZERO ONE TWO THREE FOUR FIVE SIX SEVEN EIGHT NINE

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
Z
=
8
1
1
Z
8
8
8
-
-
-
-
-
-
-
-
8
-
E
=
5
2
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
R
=
9
3
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
O
=
6
4
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
O
=
6
5
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
N
=
5
6
1
N
14
5
5
-
-
-
-
-
5
-
-
-
-
E
=
5
7
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
T
=
2
8
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
W
=
5
9
1
W
23
5
5
-
-
-
-
-
5
-
-
-
-
O
=
6
10
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
T
=
2
11
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
H
=
8
12
1
H
8
8
8
-
-
-
-
-
-
-
-
8
-
R
=
9
13
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
E
=
5
14
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
E
=
5
15
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
F
=
6
16
1
F
6
6
6
-
-
-
-
-
-
6
-
-
-
O
=
6
17
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
U
=
3
18
1
U
21
3
3
-
-
-
3
-
-
-
-
-
-
R
=
9
19
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
F
=
6
20
1
F
6
6
6
-
-
-
-
-
-
6
-
-
-
I
=
9
21
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
V
=
4
22
1
V
22
4
4
-
-
-
-
4
-
-
-
-
-
E
=
5
23
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
S
=
1
24
1
S
19
10
1
-
1
-
-
-
-
-
-
-
-
I
=
9
25
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
X
=
6
26
1
X
24
6
6
-
-
-
-
-
-
6
-
-
-
S
=
1
27
1
S
19
10
1
-
1
-
-
-
-
-
-
-
-
E
=
5
28
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
V
=
4
29
1
V
22
4
4
-
-
-
-
4
-
-
-
-
-
E
=
5
30
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
N
=
5
31
1
N
14
5
5
-
-
-
-
-
5
-
-
-
-
E
=
5
32
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
I
=
9
33
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
G
=
7
34
1
G
7
7
7
-
-
-
-
-
-
-
7
-
-
H
=
8
35
1
H
8
8
8
-
-
-
-
-
-
-
-
8
-
T
=
2
36
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
N
=
5
37
1
N
14
5
5
-
-
-
-
-
5
-
-
-
-
I
=
9
38
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
N
=
5
39
1
N
14
5
5
-
-
-
-
-
5
-
-
-
-
E
=
5
40
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
45
-
40
First Total
522
243
225
-
2
6
3
8
70
42
7
24
63
-
-
4+5
-
4+0
Add to Reduce
5+2+2
2+4+3
2+2+5
-
-
-
-
-
7+0
4+2
-
2+4
6+3
-
-
9
-
4
Second Total
9
9
9
-
2
6
3
8
7
6
7
6
9
-
-
-
-
-
Reduce to Deduce
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
-
4
Essence of Number
9
9
9
-
2
6
3
8
7
6
7
6
9

 

 

ZERO ONE TWO THREE FOUR FIVE SIX SEVEN EIGHT NINE

ZERO ONE TWO THREE FOUR FIVE SIX SEVEN EIGHT NINE

ZERO ONE TWO THREE FOUR FIVE SIX SEVEN EIGHT NINE

ZERO ONE TWO THREE FOUR FIVE SIX SEVEN EIGHT NINE

ZERO ONE TWO THREE FOUR FIVE SIX SEVEN EIGHT NINE

ZERO ONE TWO THREE FOUR FIVE SIX SEVEN EIGHT NINE

ZERO ONE TWO THREE FOUR FIVE SIX SEVEN EIGHT NINE

ZERO ONE TWO THREE FOUR FIVE SIX SEVEN EIGHT NINE

ZERO ONE TWO THREE FOUR FIVE SIX SEVEN EIGHT NINE

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
S
=
1
1
1
S
19
10
1
-
1
-
-
-
-
-
-
-
-
S
=
1
2
1
S
19
10
1
-
1
-
-
-
-
-
-
-
-
T
=
2
3
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
T
=
2
4
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
T
=
2
5
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
U
=
3
6
1
U
21
3
3
-
-
-
3
-
-
-
-
-
-
V
=
4
7
1
V
22
4
4
-
-
-
-
4
-
-
-
-
-
V
=
4
8
1
V
22
4
4
-
-
-
-
4
-
-
-
-
-
E
=
5
9
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
N
=
5
10
1
N
14
5
5
-
-
-
-
-
5
-
-
-
-
E
=
5
11
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
W
=
5
12
1
W
23
5
5
-
-
-
-
-
5
-
-
-
-
E
=
5
13
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
E
=
5
14
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
E
=
5
15
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
E
=
5
16
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
E
=
5
17
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
N
=
5
18
1
N
14
5
5
-
-
-
-
-
5
-
-
-
-
E
=
5
19
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
N
=
5
20
1
N
14
5
5
-
-
-
-
-
5
-
-
-
-
N
=
5
21
1
N
14
5
5
-
-
-
-
-
5
-
-
-
-
E
=
5
22
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
O
=
6
23
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
O
=
6
24
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
O
=
6
25
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
F
=
6
26
1
F
6
6
6
-
-
-
-
-
-
6
-
-
-
O
=
6
27
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
F
=
6
28
1
F
6
6
6
-
-
-
-
-
-
6
-
-
-
X
=
6
29
1
X
24
6
6
-
-
-
-
-
-
6
-
-
-
G
=
7
30
1
G
7
7
7
-
-
-
-
-
-
-
7
-
-
Z
=
8
31
1
Z
8
8
8
-
-
-
-
-
-
-
-
8
-
H
=
8
32
1
H
8
8
8
-
-
-
-
-
-
-
-
8
-
H
=
8
33
1
H
8
8
8
-
-
-
-
-
-
-
-
8
-
R
=
9
34
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
R
=
9
35
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
R
=
9
36
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
I
=
9
37
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
I
=
9
38
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
I
=
9
39
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
I
=
9
40
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
45
-
40
First Total
522
243
225
-
2
6
3
8
70
42
7
24
63
-
-
4+5
-
4+0
Add to Reduce
5+2+2
2+4+3
2+2+5
-
-
-
-
-
7+0
4+2
-
2+4
6+3
-
-
9
-
4
Second Total
9
9
9
-
2
6
3
8
7
6
7
6
9
-
-
-
-
-
Reduce to Deduce
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
-
4
Essence of Number
9
9
9
-
2
6
3
8
7
6
7
6
9

 

 

ZERO ONE TWO THREE FOUR FIVE 1IX 1EVEN EIGHT NINE

ZERO ONE 2WO 2HREE FOUR FIVE SIX SEVEN EIGH2 NINE

ZERO ONE TWO THREE FO3R FIVE SIX SEVEN EIGHT NINE

ZERO ONE TWO THREE FOUR FI4E SIX SE4EN EIGHT NINE

Z5RO O55 T5O THR55 FOUR FIV5 SIX S5V55 5IGHT 5I55

ZER6 6NE TW6 THREE 66UR 6IVE SI6 SEVEN EIGHT NINE

ZERO ONE TWO THREE FOUR FIVE SIX SEVEN EI7HT NINE

8ERO ONE TWO T8REE FOUR FIVE SIX SEVEN EIG8T NINE

ZE9O ONE TWO TH9EE FOU9 F9VE S9X SEVEN E9GHT N9NE

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
Z
=
8
1
1
Z
8
8
8
-
-
-
-
-
-
-
-
8
-
E
=
5
2
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
R
=
9
3
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
O
=
6
4
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
O
=
6
5
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
N
=
5
6
1
N
14
5
5
-
-
-
-
-
5
-
-
-
-
E
=
5
7
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
T
=
2
8
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
W
=
5
9
1
W
23
5
5
-
-
-
-
-
5
-
-
-
-
O
=
6
10
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
T
=
2
11
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
H
=
8
12
1
H
8
8
8
-
-
-
-
-
-
-
-
8
-
R
=
9
13
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
E
=
5
14
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
E
=
5
15
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
F
=
6
16
1
F
6
6
6
-
-
-
-
-
-
6
-
-
-
O
=
6
17
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
U
=
3
18
1
U
21
3
3
-
-
-
3
-
-
-
-
-
-
R
=
9
19
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
F
=
6
20
1
F
6
6
6
-
-
-
-
-
-
6
-
-
-
I
=
9
21
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
V
=
4
22
1
V
22
4
4
-
-
-
-
4
-
-
-
-
-
E
=
5
23
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
S
=
1
24
1
S
19
10
1
-
1
-
-
-
-
-
-
-
-
I
=
9
25
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
X
=
6
26
1
X
24
6
6
-
-
-
-
-
-
6
-
-
-
S
=
1
27
1
S
19
10
1
-
1
-
-
-
-
-
-
-
-
E
=
5
28
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
V
=
4
29
1
V
22
4
4
-
-
-
-
4
-
-
-
-
-
E
=
5
30
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
N
=
5
31
1
N
14
5
5
-
-
-
-
-
5
-
-
-
-
E
=
5
32
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
I
=
9
33
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
G
=
7
34
1
G
7
7
7
-
-
-
-
-
-
-
7
-
-
H
=
8
35
1
H
8
8
8
-
-
-
-
-
-
-
-
8
-
T
=
2
36
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
N
=
5
37
1
N
14
5
5
-
-
-
-
-
5
-
-
-
-
I
=
9
38
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
N
=
5
39
1
N
14
5
5
-
-
-
-
-
5
-
-
-
-
E
=
5
40
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
45
-
40
First Total
522
243
225
-
2
6
3
8
70
42
7
24
63
-
-
4+5
-
4+0
Add to Reduce
5+2+2
2+4+3
2+2+5
-
-
-
-
-
7+0
4+2
-
2+4
6+3
-
-
9
-
4
Second Total
9
9
9
-
2
6
3
8
7
6
7
6
9
-
-
-
-
-
Reduce to Deduce
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
-
4
Essence of Number
9
9
9
-
2
6
3
8
7
6
7
6
9

 

 

ZERO ONE TWO THREE FOUR FIVE SIX SEVEN EIGHT NINE

8596 655 256 28955 6639 6945 196 15455 59782 5955

ZERO ONE TWO THREE FOUR FIVE SIX SEVEN EIGHT NINE

 

 

ZERO ONE TWO THREE FOUR FIVE SIX SEVEN EIGHT NINE

8596 655 256 28955 6639 6945 196 15455 59782 5955

8596 655 256 28955 6639 6945 196 15455 59782 5955

8596 655 256 28955 6639 6945 196 15455 59782 5955

8596 655 256 28955 6639 6945 196 15455 59782 5955

8596 655 256 28955 6639 6945 196 15455 59782 5955

8596 655 256 28955 6639 6945 196 15455 59782 5955

8596 655 256 28955 6639 6945 196 15455 59782 5955

8596 655 256 28955 6639 6945 196 15455 59782 5955

8596 655 256 28955 6639 6945 196 15455 59782 5955

ZERO ONE TWO THREE FOUR FIVE SIX SEVEN EIGHT NINE

 

 

-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
0
-
Z
=
8
1
4
ZERO
64
28
1
-
1
-
-
-
-
-
-
-
-
1
-
O
=
6
2
3
ONE
34
16
7
-
-
-
-
-
-
-
7
-
-
2
-
T
=
2
3
3
TWO
58
13
4
-
-
-
-
4
-
-
-
-
-
3
-
T
=
2
4
5
THREE
56
29
2
-
-
2
-
-
-
-
-
-
-
4
-
F
=
6
5
4
FOUR
60
24
6
-
-
-
-
-
-
6
-
-
-
5
-
F
=
6
6
4
FIVE
42
24
6
-
-
-
-
-
-
6
-
-
-
6
-
S
=
1
7
3
SIX
52
16
7
-
-
-
-
-
-
-
7
-
-
7
-
S
=
1
8
5
SEVEN
65
20
2
-
-
2
-
-
-
-
-
-
-
8
-
E
=
5
9
5
EIGHT
49
31
4
-
-
-
-
4
-
-
-
-
-
9
-
N
=
5
10
4
NINE
42
24
6
-
-
-
-
-
-
6
-
-
-
45
-
-
-
42
-
40
Add
522
225
45
-
1
4
3
8
5
18
14
8
9
4+5
-
-
-
4+2
-
4+0
Reduce
5+2+2
2+2+5
4+5
-
-
-
-
-
-
1+8
1+4
-
-
9
-
-
-
6
-
4
Deduce
9
9
9
-
1
4
3
8
5
9
5
8
9

 

 

-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
0
-
Z
=
8
1
4
ZERO
64
28
1
-
1
-
-
-
-
-
-
-
-
3
-
T
=
2
2
5
THREE
56
29
2
-
-
2
-
-
-
-
-
-
-
7
-
S
=
1
3
5
SEVEN
65
20
2
-
-
2
-
-
-
-
-
-
-
1
-
O
=
6
4
3
ONE
34
16
7
-
-
-
-
-
-
-
7
-
-
2
-
T
=
2
5
3
TWO
58
13
4
-
-
-
-
4
-
-
-
-
-
8
-
E
=
5
6
5
EIGHT
49
31
4
-
-
-
-
4
-
-
-
-
-
4
-
F
=
6
7
4
FOUR
60
24
6
-
-
-
-
-
-
6
-
-
-
5
-
F
=
6
8
4
FIVE
42
24
6
-
-
-
-
-
-
6
-
-
-
9
-
N
=
5
9
4
NINE
42
24
6
-
-
-
-
-
-
6
-
-
-
6
-
S
=
1
10
3
SIX
52
16
7
-
-
-
-
-
-
-
7
-
-
45
-
-
-
42
-
40
Add
522
225
45
-
1
4
3
8
5
18
14
8
9
4+5
-
-
-
4+2
-
4+0
Reduce
5+2+2
2+2+5
4+5
-
-
-
-
-
-
1+8
1+4
-
-
9
-
-
-
6
-
4
Deduce
9
9
9
-
1
4
3
8
5
9
5
8
9

 

 

-
-
-
-
-
-
-
-
-
-
-
-
1
2
4
6
7
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
0
-
Z
=
8
1
4
ZERO
64
28
1
-
1
-
-
-
-
3
-
T
=
2
2
5
THREE
56
29
2
-
-
2
-
-
-
7
-
S
=
1
3
5
SEVEN
65
20
2
-
-
2
-
-
-
1
-
O
=
6
4
3
ONE
34
16
7
-
-
-
-
-
7
2
-
T
=
2
5
3
TWO
58
13
4
-
-
-
4
-
-
8
-
E
=
5
6
5
EIGHT
49
31
4
-
-
-
4
-
-
4
-
F
=
6
7
4
FOUR
60
24
6
-
-
-
-
6
-
5
-
F
=
6
8
4
FIVE
42
24
6
-
-
-
-
6
-
9
-
N
=
5
9
4
NINE
42
24
6
-
-
-
-
6
-
6
-
S
=
1
10
3
SIX
52
16
7
-
-
-
-
-
7
45
-
-
-
42
-
40
Add
522
225
45
-
1
4
8
18
14
4+5
-
-
-
4+2
-
4+0
Reduce
5+2+2
2+2+5
4+5
-
-
-
-
1+8
1+4
9
-
-
-
6
-
4
Deduce
9
9
9
-
1
4
8
9
5

 

 

-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
0
-
Z
=
8
1
4
ZERO
64
28
1
-
1
-
-
-
-
-
-
-
-
1
-
O
=
6
2
3
ONE
34
16
7
-
-
-
-
-
-
-
7
-
-
2
-
T
=
2
3
3
TWO
58
13
4
-
-
-
-
4
-
-
-
-
-
3
-
T
=
2
4
5
THREE
56
29
2
-
-
2
-
-
-
-
-
-
-
4
-
F
=
6
5
4
FOUR
60
24
6
-
-
-
-
-
-
6
-
-
-
5
-
F
=
6
6
4
FIVE
42
24
6
-
-
-
-
-
-
6
-
-
-
6
-
S
=
1
7
3
SIX
52
16
7
-
-
-
-
-
-
-
7
-
-
7
-
S
=
1
8
5
SEVEN
65
20
2
-
-
2
-
-
-
-
-
-
-
8
-
E
=
5
9
5
EIGHT
49
31
4
-
-
-
-
4
-
-
-
-
-
9
-
N
=
5
10
4
NINE
42
24
6
-
-
-
-
-
-
6
-
-
-
45
-
-
-
42
-
40
Add
522
225
45
-
1
4
3
8
5
18
14
8
9
4+5
-
-
-
4+2
-
4+0
Reduce
5+2+2
2+2+5
4+5
-
-
-
-
-
-
1+8
1+4
-
-
9
-
-
-
6
-
4
Deduce
9
9
9
-
1
4
3
8
5
9
5
8
9

 

 

THE LIGHT IS RISING NOW RISING IS THE LIGHT

 

 

-
THE RAINBOW LIGHT
-
-
-
3
THE
33
15
6
7
RAINBOW
82
37
1
5
LIGHT
56
29
2
15
THE RAINBOW LIGHT
171
81
9
1+5
-
1+7+1
8+1
-
6
THE RAINBOW LIGHT
9
9
9

 

 

15
THE RAINBOW LIGHT
-
-
-
-
THE
33
15
6
-
R
18
9
9
-
A
1
1
1
-
I
9
9
9
-
N+B+O+W
54
18
9
-
L
12
3
3
-
I
9
9
9
-
G+H+T
35
17
8
15
THE RAINBOW LIGHT
171
81
54
1+5
-
1+7+1
8+1
5+4
6
THE RAINBOW LIGHT
9
9
9

 

 

-
THE SOLAR SYSTEM
-
-
-
3
THE
33
15
6
5
SOLAR
65
29
2
6
SYSTEM
101
38
2
14
THE SOLAR SYSTEM
199
82
10
1+4
-
1+9+9
8+2
1+0
5
THE SOLAR SYSTEM
19
10
1
-
-
1+9
1+0
-
5
THE SOLAR SYSTEM
10
1
1
-
-
1+0
-
-
5
THE SOLAR SYSTEM
1
1
1

 

 

3
SUN
54
9
9
7
MERCURY
103
40
4
5
VENUS
81
18
9
5
EARTH
52
25
7
4
MOON
57
21
3
4
MARS
51
15
6
7
JUPITER
99
36
9
6
SATURN
93
21
3
6
URANUS
94
22
4
7
NEPTUNE
95
32
5
5
PLUTO
84
21
3
59
First Total
863
260
62
5+9
Add to Reduce
8+6+3
2+6
6+2
14
Second Total
17
8
8
1+4
Reduce to Deduce
1+7
-
-
5
Essence of Number
8
8
8

 

 

3
SUN
54
9
9
5
EARTH
52
25
7
4
MOON
57
21
3
12
First Total
163
55
19
1+2
Add to Reduce
1+6+3
5+5
1+9
3
Second Total
10
10
10
-
Reduce to Deduce
1+0
1+0
1+0
3
Essence of Number
1
1
1

 

 

26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
8
9
-
-
-
-
5
6
-
-
-
1
-
-
-
-
6
-
8
+
=
43
4+3
=
7
-
7
-
7
-
-
-
-
-
-
-
-
8
9
-
-
-
-
14
15
-
-
-
19
-
-
-
-
24
-
26
+
=
115
1+1+5
=
7
-
7
-
7
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
-
-
1
2
3
4
-
-
7
8
9
-
2
3
4
5
-
7
-
+
=
83
8+3
=
11
1+1
2
-
2
-
1
2
3
4
5
6
7
-
-
10
11
12
13
-
-
16
17
18
-
20
21
22
23
-
25
-
+
=
236
2+3+6
=
11
1+1
2
-
2
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
+
=
351
3+5+1
=
9
-
9
-
9
-
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
+
=
126
1+2+6
=
9
-
9
-
9
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
+
=
1
occurs
x
3
=
3
-
3
-
-
2
-
-
-
-
-
-
-
-
2
-
-
-
-
-
-
-
-
2
-
-
-
-
-
-
+
=
2
occurs
x
3
=
6
-
6
-
-
-
3
-
-
-
-
-
-
-
-
3
-
-
-
-
-
-
-
-
3
-
-
-
-
-
+
=
3
occurs
x
3
=
9
-
9
-
-
-
-
4
-
-
-
-
-
-
-
-
4
-
-
-
-
-
-
-
-
4
-
-
-
-
+
=
4
occurs
x
3
=
12
1+2
3
-
-
-
-
-
5
-
-
-
-
-
-
-
-
5
-
-
-
-
-
-
-
-
5
-
-
-
+
=
5
occurs
x
3
=
15
1+5
6
-
-
-
-
-
-
6
-
-
-
-
-
-
-
-
6
-
-
-
-
-
-
-
-
6
-
-
+
=
6
occurs
x
3
=
18
1+8
9
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
-
7
-
+
=
7
occurs
x
3
=
21
2+1
3
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
8
+
=
8
occurs
x
3
=
24
2+4
6
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
+
=
9
occurs
x
2
=
18
1+8
9
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
45
-
-
26
-
126
-
54
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
4+5
-
-
2+6
-
1+2+6
-
5+4
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
9
-
-
8
-
9
-
9
-
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
-
-
-
-
-
-
-
-
-
-
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
9
-
-
8
-
9
-
9

 

 

THE LIGHT IS RISING RISING IS THE LIGHT

 

 

9
LANGUAGES
87
33
6
3
AND
19
10
1
7
NUMBERS
92
29
2
19
-
198
72
9
1+9
-
1+9+8
7+2
-
10
-
18
9
9
1+0
-
1+8
-
-
1
-
9
9
9

 

 

L
=
3
-
8
LANGUAGE
68
32
5
T
=
2
-
7
TALKING
74
29
2
N
=
5
-
7
NUMBERS
92
29
2
-
=
10
-
22
-
234
90
9
-
=
1+0
-
2+2
-
2+3+4
9+0
-
-
=
1
-
4
-
9
9
9

 

 

T
=
2
-
9
THE
33
15
6
E
=
5
-
3
ENGLISH
74
29
2
A
=
1
-
7
ALPHABET
65
29
2
-
-
8
-
19
-
172
73
10
-
-
4+6
-
1+9
-
1+7+2
7+3
1+0
-
-
8
-
10
-
10
10
1
-
-
-
-
1+0
-
1+0
1+0
-
-
-
8
-
1
-
1
1
1

 

 

-
-
-
-
-
LANGUAGE
-
-
-
L
=
3
-
2
L+A+N
27
9
9
A
=
1
-
2
G+U+A+G
18
18
9
N
=
5
-
3
E
5
5
5
-
-
32
-
8
LANGUAGE
68
32
32
-
-
3+2
-
-
-
6+8
3+2
3+2
-
-
5
-
8
LANGUAGE
14
5
5
-
-
-
-
-
-
1+4
-
-
-
-
5
-
8
LANGUAGE
5
5
5

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
LANGUAGE
-
-
-
-
-
-
-
-
-
-
-
-
-
L
=
3
-
2
L
12
3
3
-
-
-
3
-
-
-
-
-
-
A
=
1
-
2
A
1
1
1
-
1
-
-
-
-
-
-
-
-
N
=
5
-
3
N
14
5
5
-
-
-
-
-
5
-
-
-
-
G
=
7
-
2
G
7
7
7
-
-
-
-
-
-
-
7
-
-
U
=
3
-
3
U
21
3
3
-
-
-
3
-
-
-
-
-
-
A
=
1
-
3
A
1
1
1
-
1
-
-
-
-
-
-
-
-
G
=
7
-
4
G
7
7
7
-
-
-
-
-
-
-
7
-
-
E
=
5
-
3
E
5
5
5
-
-
-
-
-
5
-
-
-
-
-
-
32
-
8
LANGUAGE
68
32
32
-
2
2
6
4
10
6
14
8
9
-
-
3+2
-
-
-
6+8
3+2
3+2
-
-
-
-
-
1+0
-
1+4
-
-
-
-
5
-
8
LANGUAGE
14
5
5
-
2
2
6
4
1
6
5
8
9
-
-
-
-
-
-
1+4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
5
-
8
LANGUAGE
5
5
5
-
2
2
6
4
1
6
5
8
9

 

 

D
=
4
-
-
DICTIONARY
-
-
-
-
-
-
-
1
D
4
4
4
-
-
-
-
1
I
9
9
9
-
-
-
-
1
C
3
3
3
-
-
-
-
1
T
20
2
2
-
-
-
-
1
I
9
9
9
-
-
-
-
1
O
15
6
6
-
-
-
-
1
N
14
5
5
-
-
-
-
1
A
1
1
1
-
-
-
-
1
R
18
9
9
-
-
-
-
1
Y
25
7
7
D
=
4
Q
10
DICTIONARY
118
55
55
-
-
-
-
1+0
-
1+1+8
5+5
5+5
D
=
4
Q
1
DICTIONARY
10
10
10
-
-
-
-
-
-
1+0
1+0
1+0
D
=
4
Q
1
DICTIONARY
1
1
1

 

 

D
=
4
-
-
DICTIONARY
-
-
-
-
-
-
-
1
A
1
1
1
-
-
-
-
1
T
20
2
2
-
-
-
-
1
C
3
3
3
-
-
-
-
1
D
4
4
4
-
-
-
-
1
N
14
5
5
-
-
-
-
1
O
15
6
6
-
-
-
-
1
Y
25
7
7
-
-
-
-
1
I
9
9
9
-
-
-
-
1
I
9
9
9
-
-
-
-
1
R
18
9
9
D
=
4
Q
10
DICTIONARY
118
55
55
-
-
-
-
1+0
-
1+1+8
5+5
5+5
D
=
4
Q
1
DICTIONARY
10
10
10
-
-
-
-
-
-
1+0
1+0
1+0
D
=
4
Q
1
DICTIONARY
1
1
1

 

 

D
=
4
-
-
DICTIONARY
-
-
-
-
-
-
-
1
D
4
4
4
-
-
-
-
1
I
9
9
9
-
-
-
-
1
C+T
23
5
5
-
-
-
-
1
I
9
9
9
-
-
-
-
1
O+N+A
30
12
3
-
-
-
-
1
R
18
9
9
-
-
-
-
1
Y
25
7
7
D
=
4
Q
10
DICTIONARY
118
55
46
-
-
-
-
1+0
-
1+1+8
5+5
4+6
D
=
4
Q
1
DICTIONARY
10
10
10
-
-
-
-
-
-
1+0
1+0
-
D
=
4
Q
1
DICTIONARY
1
1
1

 

 

-
-
-
-
-

DICTIONARY
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
D
=
4
1
1
D
4
4
4
-
-
-
-
4
-
-
-
8
-
I
=
9
2
1
I
9
9
9
-
-
-
-
-
-
-
-
8
9
C
=
3
3
1
C
3
3
3
-
-
-
3
-
-
-
-
8
-
T
=
2
4
1
T
20
2
2
-
-
2
-
-
-
-
-
8
-
I
=
9
5
1
I
9
9
9
-
-
-
-
-
-
-
-
8
9
O
=
6
6
1
O
15
6
6
-
-
-
-
-
-
6
-
8
-
N
=
5
7
1
N
14
5
5
-
-
-
-
-
5
-
-
8
-
A
=
1
8
1
A
1
1
1
-
1
-
-
-
-
-
-
8
-
R
=
9
9
1
R
18
9
9
-
-
-
-
-
-
-
-
8
9
Y
=
7
10
1
Y
25
7
7
-
-
-
-
-
-
-
7
8
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
D
=
4
-
10
DICTIONARY
118
55
55
-
1
2
3
4
5
6
7
8
27
-
-
-
-
1+0
-
1+1+8
5+5
5+5
-
-
-
-
-
-
-
-
-
2+7
D
=
4
-
1
DICTIONARY
10
10
10
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
1+0
1+0
1+0
-
-
-
-
-
-
-
-
-
-
D
=
4
-
1
DICTIONARY
1
1
1
-
1
2
3
4
5
6
7
8
9

 

 

-
-
-
-
-

DICTIONARY
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
A
=
1
8
1
A
1
1
1
-
1
-
-
-
-
-
-
8
-
T
=
2
4
1
T
20
2
2
-
-
2
-
-
-
-
-
8
-
C
=
3
3
1
C
3
3
3
-
-
-
3
-
-
-
-
8
-
D
=
4
1
1
D
4
4
4
-
-
-
-
4
-
-
-
8
-
N
=
5
7
1
N
14
5
5
-
-
-
-
-
5
-
-
8
-
O
=
6
6
1
O
15
6
6
-
-
-
-
-
-
6
-
8
-
Y
=
7
10
1
Y
25
7
7
-
-
-
-
-
-
-
7
8
-
I
=
9
2
1
I
9
9
9
-
-
-
-
-
-
-
-
8
9
I
=
9
5
1
I
9
9
9
-
-
-
-
-
-
-
-
8
9
R
=
9
9
1
R
18
9
9
-
-
-
-
-
-
-
-
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
D
=
4
-
10
DICTIONARY
118
55
55
-
1
2
3
4
5
6
7
8
27
-
-
-
-
1+0
-
1+1+8
5+5
5+5
-
-
-
-
-
-
-
-
-
2+7
D
=
4
-
1
DICTIONARY
10
10
10
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
1+0
1+0
1+0
-
-
-
-
-
-
-
-
-
-
D
=
4
-
1
DICTIONARY
1
1
1
-
1
2
3
4
5
6
7
8
9

 

LETTERS TRANSPOSED INTO NUMBER REARRANGED IN NUMERICAL ORDER

 

THE

DICTIONARY

 

-
-
-
-
-

THE DICTIONARY
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
T
=
2
1
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
H
=
8
2
1
H
8
8
8
-
-
-
-
-
-
-
-
8
-
E
=
5
3
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
-
-
15
-
3
-
33
15
15
-
-
-
-
-
-
-
-
-
-
D
=
4
4
1
D
4
4
4
-
-
-
-
4
-
-
-
-
-
I
=
9
5
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
C
=
3
6
1
C
3
3
3
-
-
-
3
-
-
-
-
-
-
T
=
2
7
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
I
=
9
8
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
O
=
6
9
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
N
=
5
10
1
N
14
5
5
-
-
-
-
-
5
-
-
-
-
A
=
1
11
1
A
1
1
1
-
1
-
-
-
-
-
-
-
-
R
=
9
12
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
Y
=
7
13
1
Y
25
7
7
-
-
-
-
-
-
-
7
-
-
-
-
55
-
10
-
118
55
55
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
13
THE DICTIONARY
151
70
70
-
1
4
3
4
10
6
7
8
27
-
-
-
-
1+3
-
1+5+1
7+0
7+0
-
-
-
-
-
1+0
-
-
-
2+7
-
-
-
-
4
THE DICTIONARY
7
7
7
-
1
4
3
4
1
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
4
THE DICTIONARY
7
7
7
-
1
4
3
4
5
6
7
8
9

 

 

-
-
-
-
-

THE DICTIONARY
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
A
=
1
11
1
A
1
1
1
-
1
-
-
-
-
-
-
-
-
T
=
2
1
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
T
=
2
7
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
C
=
3
6
1
C
3
3
3
-
-
-
3
-
-
-
-
-
-
D
=
4
4
1
D
4
4
4
-
-
-
-
4
-
-
-
-
-
E
=
5
3
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
N
=
5
10
1
N
14
5
5
-
-
-
-
-
5
-
-
-
-
O
=
6
9
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
Y
=
7
13
1
Y
25
7
7
-
-
-
-
-
-
-
7
-
-
H
=
8
2
1
H
8
8
8
-
-
-
-
-
-
-
-
8
-
I
=
9
5
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
I
=
9
8
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
R
=
9
12
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
13
THE DICTIONARY
151
70
70
-
1
4
3
4
10
6
7
8
27
-
-
-
-
1+3
-
1+5+1
7+0
7+0
-
-
-
-
-
1+0
-
-
-
2+7
-
-
-
-
4
THE DICTIONARY
7
7
7
-
1
4
3
4
1
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
4
THE DICTIONARY
7
7
7
-
1
4
3
4
5
6
7
8
9

 

LETTERS TRANSPOSED INTO NUMBER REARRANGED IN NUMERICAL ORDER

 

 

T
=
2
Q
3
THE
33
15
6
E
=
5
Q
7
ENGLISH
74
38
2
D
=
4
Q
10
DICTIONARY
118
55
1
-
-
11
Q
20
Add to Reduce
225
108
9
Q
Q
1+1
-
2+0
Reduce to Deduce
1+1+8
1+0+8
-
-
-
2
Q
2
Essence of Number
9
9
9

 

 

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z =351= Z Y X W V U T S R Q P O N M L K J I H G F E D C B A

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z =126= Z Y X W V U T S R Q P O N M L K J I H G F E D C B A

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z =9= Z Y X W V U T S R Q P O N M L K J I H G F E D C B A

 

 

ABCDEFGH I JKLMNOPQ R STUVWXYZ =351= ZYXWVUTS R QPONMLKJ I HGFEDCBA

ABCDEFGH I JKLMNOPQ R STUVWXYZ =126= ZYXWVUTS R QPONMLKJ I HGFEDCBA

ABCDEFGH I JKLMNOPQ R STUVWXYZ =9= ZYXWVUTS R QPONMLKJ I HGFEDCBA

 

 

DAILY MAIL

Monday, October 8, 2007

Harry Bingham

Page 15

"YOU SAY POTATO, I SAY GHOUGHBTEIGHPTEAU !"

"...Yes you CAN spell potato like that. It's one of the amazing quirks which make English the world's dominant language

 

"ABOUT three years ago I started researching a book, This Little Britain, about the various ways in which we Brits have a history .
of being the exception.
In areas such as law, government, economics, agriculture and science, we've often been a uniquely British exception to a general European rule.
Ditto, in such things as men's fashion, Victorian sewers, drunken yobbishness, and - not least - in the whole area of language and literature.
Take spellings. George Bernard Shaw famously commented that English spelling would allow you to write the word 'fish' as 'ghoti' - and it would sound the same (in the latter, the sound 'f' would be from 'gh', as in 'rough'; 'i' would be from 'o' in 'women' and 'sh' as in 'ti' from 'nation').
But he couldn't have been trying all that hard, if that was the best example he came up with. How about 'potato' as in
'ghoughbteighpteau'? That's the sound 'p' as in hiccough, 'o' as in though, 't' as in debt, 'a' as in neighbour, 't' as in ptomaine, 'o' as in bureau. The fact is that with just 26 letters and 48 different sounds to cope with, there were always going to be problems. :
Throw in other pronunciation changes and an appetite for foreign borrowings, and it's no surprise that English has some of the most dangerously unpredictable spellings in the world.
If our spellings are painful, however, our grammar has its blessedly simple side. French nouns are either masculine or feminine; French verbs vary with every puff of the syntactical breeze.
But French is a pretty simple language. Italian has 50 different forms for every verb, ancient Greek more than 300, modern Turkish an eye popping two million. English, by contrast, has just four verb forms (bark, barks, barking, barked), two noun forms (dog, dogs), and just one adjectival form (snappy), thus making our language about the least inflected in the world.
If that's a curious fact, the reason why is perhaps odder still. Back in Alfred the Great's England, two language communities - English and Danish - inter­mingled. Each community could make out the basic words of the other language.

FOR example, the word 'horse' is 'hors' in Old English, 'hossit' in Old Norse. But all those tricksy little word endings would have made no sense at all. So they began to vanish.
Under pressure of trade, friendship and intermarriage, our ancient ancestors did away with inflections almost completely. Confusing at the time, no doubt, but a blessing for those who need to learn the language today.
And there are plenty of people learning it, of course. With about one-and a-half billion non-native speakers, English has become the world's own language - one that accounts for two-thirds of internet content, and a still larger proportion of the world's scientific and technical journals.
It's sometimes suggested that English has achieved its leadership because it's thelanguage of Shakespeare, . because of its unique and beautiful literature.
That's nonsense, of course. English dominates because the British Isles exported English speakers and gunboats in the 19th century, and because America exported Hollywood, GIs and hamburgers in the 20th.
If those Mayflower settlers had chanced to speak Ubykh (a Caucasian language with 81 consonants and 'three vowels) or Rotokas (a Papua New Guinea language with just six consonants and five vowels), the world would most likely be speaking those fine languages today.
Such dominance has its down­side, of course. There are now about 6,800 languages left in the world, compared with perhaps twice that number back at the dawn of agriculture. The remaining languages are now dying at the rate of about one a fortnight.
English is big in other ways too. If you wanted to learn all the words in the Oxford English Dictionary, you'd have to deal with about 500,000 of them (ending with zyxt, a splendid last word by any standards and an archaic Kentish term for thou seest).
Having done that, you'd probably be a bit taken aback to learn the equivalent American dictionary, Webster's, offers a further 450,000 words or so, of which only about half are to be found in the OED, suggesting a pooled total word count of about 750,000.
But there are lots of words that never get in to either dictionary. Flora and fauna are mostly out. So are most acronyms, slang and dialect. Total that lot up and you'd get to a million or so. Next, you'd need to deal with scientific and technological terms, adding another million or so words.
Otherlanguages-can't keep up. The official dictionary-based word count of German is fewer than 200,000. The French word­count is fewer than 100,000. The scale of our vocabulary is impossible to explain, except by recognising that English users are reckless adopters and inventors.
In the cultural realm, however, mere size is hardly likely to impress. In tenus of Nobel Prizes for literature, the United Kingdom trots home in the bronze medal position (beaten by gold­medallist France, and the silver­gong-holder, the US.).
If, on the other hand, you were looking at the total amount of literatureproduced by the British Isles then we would come in level with France, with 13 prizes.

BUT perhaps that's to measure things the wrong way. If you look at Nobel Prizes by language, then English wins by a country mile 26 laureates vs 13 for France).

More to the point, the Nobel Prize Committee is just that: a committee. Wouldn't it be better to let the world's reading public determine which literature it favours? Alas, there are no reliable global sales figures available.
We do, however, have an index of which authors have written the most translated books. British authors romp home in four of the top five places: Agatha Christie in first, then Enid Blyton, Shakespeare and Barbara Cartland in third to fifth. (The one interloper, Frenchman Jules Verne, is in second place.)
Looking more broadly, British authors dominate the top 40, with some 14 authors on the list, compared with 11 for the United States, and 15 for the entire rest of the world put together.
The obvious conclusion: that we Brits have some natural affinity for words and literature, the way that the Germans 'do' music, or the French 'do' visual art.
Such things run both deep and ancient. The vernacular literature of Alfred the Great's England was the most developed in Europe. It's perhaps not surprising that the same is arguably still true today."

 

"YOU SAY POTATO, I SAY GHOUGHBTEIGHPTEAU !"

 

"How about 'potato' as in
'ghoughbteighpteau'?"

 

-
GHOUGHBTEIGHPTEAU
-
-
-
2
G+H
15
15
6
2
O+U
36
9
9
2
G+H
15
15
6
3
B+T+E
27
9
9
1
I
9
9
9
2
G+H
15
15
6
2
P+T
36
9
9
3
E+A+U
27
9
9
17
GHOUGHBTEIGHPTEAU
180
90
63
1+7
-
1+8+0
9+0
6+3
8
GHOUGHBTEIGHPTEAU
9
9
9

 

 

http://www.rinkworks.com/words/lettergroups.shtml

Letters can be distinguished strictly by physical representation in a number of different ways. Sometimes groups of letters are given in the form of a puzzle, and you have to figure out the rule by which they are grouped. Below are several different letter groupings, which illustrate how many letters in the alphabet possess some particular characteristic. Some of the groupings below assume a sans-serif font.

Letters Rule
AEFHIKLMNTVWXZ Letters drawn with only straight lines
COS Letters drawn with only curved lines
BDGJPQRU Letters drawn with straight and curved lines.
 
BDO Letters with no endpoints.
P Letters with one endpoint.
ACGIJLMNQRSUVWZ Letters with two endpoints.
EFTY Letters with three endpoints.
HKX Letters with four endpoints.
 
CEFGIJKLMNSTUVWXYZ Letters with no enclosed areas.
ADOPQR Letters with one enclosed area.
B Letters with two enclosed areas.
 
BCDEHIKOX Letters with horizontal symmetry.
AFGJLMNPQRSTUVWYZ Letters without horizontal symmetry.
 
AHIMOTUVWXY Letters with vertical symmetry.
BCDEFGJKLNPQRSZ Letters without vertical symmetry.
 
HIOX Letters with horizontal and vertical symmetry.
ABCDEFGJKLMNPQRSTUVWYZ Letters without horizontal and vertical symmetry.
 
HINOSXZ Letters with 180 degree rotational symmetry.
ABCDEFGJKLMPQRTUVWY Letters without 180 degree rotational symmetry.
 
BCDGIJLMNOPRSUVWZ Letters that can be drawn without taking pen off paper.
AEFHKQTXY Letters that can't be drawn without taking pen off paper.
 
COPSUVWXZ Capital letters that look like the corresponding lower case letters.
ABDEFGHIJKLMNQRTY Capital letters that don't look like the corresponding lower case letters.
 
IJ Letters that are dotted in lower case.
ABCDEFGHKLMNOPQRSTUVWXYZ Letters that aren't dotted in lower case.
 
BDFHKLT Letters that have ascenders in lower case.
ACEGIJMNOPQRSUVWXYZ Letters that have do not ascenders in lower case.
 
GJPQY Letters that have descenders in lower case.
ABCDEFHIKLMNORSTUVWXZ Letters that do not have descenders in lower case.
 
CDILMVX Letters that are Roman Numerals.
ABEFGHJKNOPQRSTUWYZ Letters that aren't Roman Numerals.
 
EHIS Letters that consist of just dots in Morse Code.
MOT Letters that consist of just dashes in Morse Code.
ABCDFGJKLNPQRUVWXYZ Letters that consist of both dots and dashes in Morse Code.

 

 

F
=
6
-
3
FOX
45
18
9
O
=
6
-
2
OF
21
12
3
F
=
6
-
5
FOXES
69
24
6
S
-
18
4
10
Add to Reduce
135
54
18
-
-
1+8
-``
1+0
Reduce to Deduce
1+3+5
5+4
1+8
S
-
9
4
1
Essence of Number
9
9
9

 

 

-
FOX
-
-
-
1
F
6
6
6
1
O
15
6
6
1
X
24
6
6
-
OF
-
-
-
1
O
15
6
6
1
F
6
6
6
-
FOXES
-
-
-
1
F
6
6
6
1
O
15
6
6
1
X
24
6
6
2
E+S
24
6
6

 

 

-
10
F
O
X
-
O
F
-
F
O
X
E
S
-
-
-
-
-
-
-
-
-
-
-
-
-
6
6
-
6
-
-
-
6
6
-
1
+
=
31
3+1
=
4
=
4
=
4
-
-
-
15
24
-
15
-
-
-
15
24
-
19
+
=
112
1+1+2
=
4
=
4
=
4
-
10
F
O
X
-
O
F
-
F
O
X
E
S
-
-
-
-
-
-
-
-
-
-
-
-
6
-
-
-
-
6
-
6
-
-
5
-
+
=
23
2+3
=
5
=
5
=
5
-
-
6
-
-
-
-
6
-
6
-
-
5
-
+
=
23
2+3
=
5
=
5
=
5
-
10
F
O
X
-
O
F
-
F
O
X
E
S
-
-
-
-
-
-
-
-
-
-
-
-
6
15
24
-
15
6
-
6
15
24
5
19
+
=
135
1+3+5
=
9
=
9
=
9
-
-
6
6
6
-
6
6
-
6
6
6
5
1
+
=
54
5+4
=
9
=
9
=
9
-
10
F
O
X
-
O
F
-
F
O
X
E
S
T
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
1
occurs
x
1
=
1
=
1
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
2
TWO
2
-
-
-
-
-
3
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
3
THREE
3
-
-
-
-
-
4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
4
FOUR
4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
5
-
-
-
5
occurs
x
1
=
5
=
5
-
-
6
6
6
-
6
6
-
6
6
6
-
-
-
-
6
occurs
x
8
=
48
=
3
7
-
-
-
-
-
-
-
-
-
-
-
-
7
-
-
7
SEVEN
7
-
-
-
-
-
8
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
8
EIGHT
8
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
NINE
9
-
-
-
-
-
33
10
F
O
X
-
O
F
-
F
O
X
E
S
-
-
12
-
-
10
-
54
-
9
3+3
1+0
6
6
6
-
6
6
-
6
6
6
5
-
-
-
1+2
-
-
1+0
-
5+4
-
-
6
1
F
O
X
-
O
F
-
F
O
X
E
S
-
-
3
-
-
1
-
9
-
9
-
-
6
6
6
-
6
6
-
6
6
6
5
1
T
-
-
-
-
-
-
-
-
-
6
1
F
O
X
-
O
F
-
F
O
X
E
S
-
-
3
-
-
1
-
9
-
9

 

 

10
F
O
X
-
O
F
-
F
O
X
E
S
-
-
-
-
-
-
-
-
-
-
-
-
6
6
-
6
-
-
-
6
6
-
1
+
=
31
3+1
=
4
=
4
=
4
-
-
15
24
-
15
-
-
-
15
24
-
19
+
=
112
1+1+2
=
4
=
4
=
4
10
F
O
X
-
O
F
-
F
O
X
E
S
-
-
-
-
-
-
-
-
-
-
-
6
-
-
-
-
6
-
6
-
-
5
-
+
=
23
2+3
=
5
=
5
=
5
-
6
-
-
-
-
6
-
6
-
-
5
-
+
=
23
2+3
=
5
=
5
=
5
10
F
O
X
-
O
F
-
F
O
X
E
S
-
-
-
-
-
-
-
-
-
-
-
6
15
24
-
15
6
-
6
15
24
5
19
+
=
135
1+3+5
=
9
=
9
=
9
-
6
6
6
-
6
6
-
6
6
6
5
1
+
=
54
5+4
=
9
=
9
=
9
10
F
O
X
-
O
F
-
F
O
X
E
S
T
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
1
occurs
x
1
=
1
=
1
-
-
-
-
-
-
-
-
-
-
-
5
-
-
-
5
occurs
x
1
=
5
=
5
-
6
6
6
-
6
6
-
6
6
6
-
-
-
-
6
occurs
x
8
=
48
=
3
10
F
O
X
-
O
F
-
F
O
X
E
S
-
-
12
-
-
10
-
54
-
9
1+0
6
6
6
-
6
6
-
6
6
6
5
-
-
-
1+2
-
-
1+0
-
5+4
-
-
1
F
O
X
-
O
F
-
F
O
X
E
S
-
-
3
-
-
1
-
9
-
9
-
6
6
6
-
6
6
-
6
6
6
5
1
T
-
-
-
-
-
-
-
-
-
1
F
O
X
-
O
F
-
F
O
X
E
S
-
-
3
-
-
1
-
9
-
9

 

 

T
=
2
-
3
THE
33
15
6
A
=
1
-
6
ANUBIS
66
21
3
-
-
3
Q
9
First Total
99
36
9
-
-
-
-
-
Add to Reduce
9+9
3+6
-
-
-
3
-
9
Second Total
18
9
9
-
-
-
-
-
Reduce to Deduce
1+8
-
-
-
-
3
-
9
Essence of Number
9
9
9

 

ANUBIS A DOG FOX IS

ANUBIS A NUMBER IS

 

F
=
6
-
3
FOX
45
18
9
O
=
6
-
2
OF
21
12
3
F
=
6
-
5
FOXES
69
24
6
-
-
18
-
10
Add to Reduce
135
54
18
-
-
1+8
--
1+0
Reduce to Deduce
1+3+5
5+4
1+8
-
-
9
-
1
Essence of Number
9
9
9

 

 

-
FOX
-
-
-
1
F
6
6
6
1
O
15
6
6
1
X
24
6
6
-
OF
-
-
-
1
O
15
6
6
1
F
6
6
6
-
FOXES
-
-
-
1
F
6
6
6
1
O
15
6
6
1
X
24
6
6
2
E+S
24
6
6

 

 

1 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 1

2 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 2

3 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 3

4 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 4

5 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 5

6 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 6

7 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 7

8 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 8

9 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 9

10 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 10

11 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 11

12 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 14

13 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 4

14 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 14

15 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 15

16 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 16

17 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 17

18 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 18

19 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 19

20 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 20

21 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 21

22 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 22

23 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 23

24 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 24

25 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 25

26 THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG 26

 

 

-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
T
=
2
-
3
THE
33
15
6
-
-
-
-
-
-
6
-
-
-
2
-
Q
=
8
-
5
QUICK
61
25
7
-
-
-
-
-
-
-
7
-
-
3
-
B
=
2
-
5
BROWN
72
27
9
-
-
-
-
-
-
-
-
-
9
4
-
F
=
6
-
3
FOX
45
18
9
-
-
-
-
-
-
-
-
-
9
5
-
J
=
1
-
5
JUMPS
79
16
7
-
-
-
-
-
-
-
7
-
-
6
-
O
=
6
-
4
OVER
60
24
6
-
-
-
-
-
-
6
-
-
-
7
-
T
=
2
-
3
THE
33
15
6
-
-
-
-
-
-
6
-
-
-
8
-
L
=
3
-
4
LAZY
64
19
1
-
1
-
-
-
-
-
-
-
-
9
-
D
=
4
-
3
DOG
26
17
8
-
-
-
-
-
-
-
-
8
-
45
-
-
-
34
-
35
Add
473
176
59
-
1
2
3
4
5
18
14
8
18
4+5
-
-
-
3+4
-
3+5
Reduce
4+7+3
1+7+6
5+9
-
-
-
-
-
-
1+8
1+4
-
1+8
9
-
-
-
7
4
8
Deduce
14
14
14
-
1
2
3
4
5
9
5
8
9
-
-
-
-
-
-
-
Produce
1+4
1+4
1+4
-
-
-
-
-
-
-
-
-
-
9
-
-
-
7
-
8
Essence
5
5
14
-
1
2
3
4
5
9
5
8
9

 

 

1 THE QUICK BROWN FOX JUMP1 OVER THE LAZY DOG 1

2 2HE QUICK BROWN FOX JUMPS OVER 2HE LAZY DOG 2

3 THE Q3I3K BROWN FOX J3MPS OVER THE 3AZY DOG 3

4 THE QUICK BROWN FOX JU4PS OVER THE LAZY 4OG 4

5 THE QUICK BRO55 FOX JUMPS OV5R TH5 LAZY DOG 5

6 THE QUICK BR6WN 666 JUMPS 6VER THE LAZY D6OG 6

7 THE QUICK BROWN FOX JUM7S OVER THE LAZ7 DO7 7

8 T8E 8UICK BROWN FOX JUMPS OVER T8E LA8Y DOG 8

9 THE QU9CK B9OWN FOX JUMPS OVE9 THE LAZY DOG 9

10 THE QUICK BROWN FOX JUMP1 OVER THE LAZY DOG 10

11 2HE QUICK BROWN FOX JUMPS OVER 2HE LAZY DOG 11

12 THE Q3I3K BROWN FOX J3MPS OVER THE 3AZY DOG 12

13 THE QUICK BROWN FOX JU4PS OVER THE LAZY 4OG 13

14 THE QUICK BRO55 FOX JUMPS OV5R TH5 LAZY DOG 14

15 THE QUICK BR6WN 666 JUMPS 6VER THE LAZY D6OG 15

16 THE QUICK BROWN FOX JUM7S OVER THE LAZ7 DO7 16

17 T8E 8UICK BROWN FOX JUMPS OVER T8E LA8Y DOG 17

18 THE QU9CK B9OWN FOX JUMPS OVE9 THE LAZY DOG 18

19 THE QUICK BROWN FOX JUMP1 OVER THE LAZY DOG 19

20 2HE QUICK BROWN FOX JUMPS OVER 2HE LAZY DOG 20

21 THE Q3I3K BROWN FOX J3MPS OVER THE 3AZY DOG 21

22 THE QUICK BROWN FOX JU4PS OVER THE LAZY 4OG 22

23 THE QUICK BRO55 FOX JUMPS OV5R TH5 LAZY DOG 23

24 THE QUICK BR6WN 666 JUMPS 6VER THE LAZY D6OG 24

25 THE QUICK BROWN FOX JUM7S OVER THE LAZ7 DO7 25

26 T8E 8UICK BROWN FOX JUMPS OVER T8E LA8Y DOG 26

 

 

The quick brown fox jumps over the lazy dog - Wikipedia ...
From Wikipedia, the free encyclopedia

"The quick brown fox jumps over the lazy dog" is an English-language pangram—a phrase that contains all of the letters of the alphabet.

"The quick brown fox jumps over the lazy dog" is an English-language pangram—a phrase that contains all of the letters of the alphabet. It is used to show fonts and to test typewriters and computer keyboards, and in other applications involving all of the letters in the English alphabet. Owing to its brevity and coherence, it has become widely known

History[edit]

The earliest known appearance of the phrase is from The Michigan School Moderator, a journal that provided many teachers with education-related news and suggestions for lessons.[1] In an article titled "Interesting Notes" in the March 14, 1885 issue, the phrase is given as a suggestion for writing practice: "The following sentence makes a good copy for practice, as it contains every letter of the alphabet: 'A quick brown fox jumps over the lazy dog.'"[2] Note that the phrase in this case begins with the word "A" rather than "The". Several other early sources also use this variation.

As the use of typewriters grew in the late 19th century, the phrase began appearing in typing and stenography lesson books as a practice sentence. Early examples of publications which used the phrase include Illustrative Shorthand by Linda Bronson (1888),[3] How to Become Expert in Typewriting: A Complete Instructor Designed Especially for the Remington Typewriter (1890),[4] and Typewriting Instructor and Stenographer's Hand-book (1892). By the turn of the 20th century, the phrase had become widely known. In the January 10, 1903, issue of Pitman's Phonetic Journal, it is referred to as "the well known memorized typing line embracing all the letters of the alphabet".[5] Robert Baden-Powell's book Scouting for Boys (1908) uses the phrase as a practice sentence for signaling.[6]

The first message sent on the Moscow–Washington hotline was the test phrase "THE QUICK BROWN FOX JUMPED OVER THE LAZY DOG'S BACK 1234567890".[7] Later, during testing, the Russian translators sent a message asking their American counterparts "What does it mean when your people say 'The quick brown fox jumped over the lazy dog?'"[8]

During the 20th century, technicians tested typewriters and teleprinters with repeated lines of "THE QUICK BROWN FOX..." sentence.[9]

 

THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG

 

 

-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
T
=
2
-
3
THE
33
15
6
-
-
-
-
-
-
6
-
-
-
2
-
Q
=
8
-
5
QUICK
61
25
7
-
-
-
-
-
-
-
7
-
-
3
-
B
=
2
-
5
BROWN
72
27
9
-
-
-
-
-
-
-
-
-
9
4
-
F
=
6
-
3
FOX
45
18
9
-
-
-
-
-
-
-
-
-
9
5
-
J
=
1
-
5
JUMPS
79
16
7
-
-
-
-
-
-
-
7
-
-
6
-
O
=
6
-
4
OVER
60
24
6
-
-
-
-
-
-
6
-
-
-
7
-
T
=
2
-
3
THE
33
15
6
-
-
-
-
-
-
6
-
-
-
8
-
L
=
3
-
4
LAZY
64
19
1
-
1
-
-
-
-
-
-
-
-
9
-
D
=
4
-
3
DOG
26
17
8
-
-
-
-
-
-
-
-
8
-
45
-
-
-
34
-
35
Add
473
176
59
-
1
2
3
4
5
18
14
8
18
4+5
-
-
-
3+4
-
3+5
Reduce
4+7+3
1+7+6
5+9
-
-
-
-
-
-
1+8
1+4
-
1+8
9
-
-
-
7
4
8
Deduce
14
14
14
-
1
2
3
4
5
9
5
8
9
-
-
-
-
-
-
-
Produce
1+4
1+4
1+4
-
-
-
-
-
-
-
-
-
-
9
-
-
-
7
-
8
Essence
5
5
14
-
1
2
3
4
5
9
5
8
9

 

 

THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
T
=
2
-
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
H
=
8
-
1
H
8
8
8
-
-
-
-
-
-
-
-
8
-
E
=
5
-
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
Q
=
8
-
1
Q
17
8
8
-
-
-
-
-
-
-
-
8
-
U
=
3
-
1
U
21
3
3
-
-
-
3
-
-
-
-
-
-
I
=
9
-
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
C
=
3
-
1
C
3
3
3
-
-
-
3
-
-
-
-
-
-
K
=
2
-
1
K
11
2
2
-
-
2
-
-
-
-
-
-
-
B
=
2
-
1
B
2
2
2
-
-
2
-
-
-
-
-
-
-
R
=
9
-
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
O
=
6
-
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
W
=
5
-
1
W
23
5
5
-
-
-
-
-
5
-
-
-
-
N
=
5
-
1
N
14
5
5
-
-
-
-
-
5
-
-
-
-
F
=
6
-
1
F
6
6
6
-
-
-
-
-
-
6
-
-
-
O
=
6
-
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
X
=
6
-
1
X
24
6
6
-
-
-
-
-
-
6
-
-
-
J
=
1
-
1
J
10
1
1
-
1
-
-
-
-
-
-
-
-
U
=
3
-
1
U
21
3
3
-
-
-
3
-
-
-
-
-
-
M
=
4
-
1
M
13
4
4
-
-
-
-
4
-
-
-
-
-
P
=
7
-
1
P
16
7
7
-
-
-
-
-
-
-
7
-
-
S
=
1
-
1
S
19
10
1
-
1
-
-
-
-
-
-
-
-
O
=
6
-
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
V
=
4
-
1
V
22
4
4
-
-
-
-
4
-
-
-
-
-
E
=
5
-
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
R
=
9
-
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
T
=
2
-
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
H
=
8
-
1
H
8
8
8
-
-
-
-
-
-
-
-
8
-
E
=
5
-
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
L
=
3
-
1
L
12
3
3
-
-
-
3
-
-
-
-
-
-
A
=
1
-
1
A
1
1
1
-
1
-
-
-
-
-
-
-
-
Z
=
8
-
1
Z
26
8
8
-
-
-
-
-
-
-
-
8
-
Y
=
5
-
1
Y
25
7
7
-
-
-
-
-
-
-
7
-
-
V
=
4
-
1
D
4
4
4
-
-
-
-
4
-
-
-
-
-
O
=
6
-
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
G
=
7
-
1
G
7
7
7
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
34
-
35
First Total
473
176
59
-
3
8
12
12
25
36
21
32
27
-
-
3+4
-
3+5
Add to Reduce
4+7+3
1+7+6
5+9
-
-
-
1+2
1+2
2+5
3+6
2+1
3+2
2+7
-
-
7
4
8
Second Total
14
14
14
-
3
8
3
3
7
9
3
5
9
-
-
-
-
-
Reduce to Deduce
1+4
1+4
1+4
-
-
-
-
-
-
-
-
-
-
-
-
7
-
8
Essence of Number
5
5
14
-
3
8
3
3
7
9
3
5
9

 

THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
J
=
1
-
1
J
10
1
1
-
1
-
-
-
-
-
-
-
-
S
=
1
-
1
S
19
10
1
-
1
-
-
-
-
-
-
-
-
A
=
1
-
1
A
1
1
1
-
1
-
-
-
-
-
-
-
-
T
=
2
-
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
K
=
2
-
1
K
11
2
2
-
-
2
-
-
-
-
-
-
-
B
=
2
-
1
B
2
2
2
-
-
2
-
-
-
-
-
-
-
T
=
2
-
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
U
=
3
-
1
U
21
3
3
-
-
-
3
-
-
-
-
-
-
C
=
3
-
1
C
3
3
3
-
-
-
3
-
-
-
-
-
-
U
=
3
-
1
U
21
3
3
-
-
-
3
-
-
-
-
-
-
L
=
3
-
1
L
12
3
3
-
-
-
3
-
-
-
-
-
-
M
=
4
-
1
M
13
4
4
-
-
-
-
4
-
-
-
-
-
V
=
4
-
1
V
22
4
4
-
-
-
-
4
-
-
-
-
-
V
=
4
-
1
D
4
4
4
-
-
-
-
4
-
-
-
-
-
E
=
5
-
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
W
=
5
-
1
W
23
5
5
-
-
-
-
-
5
-
-
-
-
N
=
5
-
1
N
14
5
5
-
-
-
-
-
5
-
-
-
-
E
=
5
-
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
E
=
5
-
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
O
=
6
-
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
F
=
6
-
1
F
6
6
6
-
-
-
-
-
-
6
-
-
-
O
=
6
-
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
X
=
6
-
1
X
24
6
6
-
-
-
-
-
-
6
-
-
-
O
=
6
-
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
O
=
6
-
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
Y
=
5
-
1
Y
25
7
7
-
-
-
-
-
-
-
7
-
-
G
=
7
-
1
G
7
7
7
-
-
-
-
-
-
-
7
-
-
P
=
7
-
1
P
16
7
7
-
-
-
-
-
-
-
7
-
-
H
=
8
-
1
H
8
8
8
-
-
-
-
-
-
-
-
8
-
Q
=
8
-
1
Q
17
8
8
-
-
-
-
-
-
-
-
8
-
H
=
8
-
1
H
8
8
8
-
-
-
-
-
-
-
-
8
-
Z
=
8
-
1
Z
26
8
8
-
-
-
-
-
-
-
-
8
-
I
=
9
-
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
R
=
9
-
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
R
=
9
-
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
34
-
35
First Total
473
176
59
-
3
8
12
12
25
36
21
32
27
-
-
3+4
-
3+5
Add to Reduce
4+7+3
1+7+6
5+9
-
-
-
1+2
1+2
2+5
3+6
2+1
3+2
2+7
-
-
7
4
8
Second Total
14
14
14
-
3
8
3
3
7
9
3
5
9
-
-
-
-
-
Reduce to Deduce
1+4
1+4
1+4
-
-
-
-
-
-
-
-
-
-
-
-
7
-
8
Essence of Number
5
5
14
-
3
8
3
3
7
9
3
5
9

 

THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG

 

 

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

 

 

PANGRAM = 7 = PANGRAM

 

-
-
-
-
-
PANGRAM
-
-
-
P
=
7
-
1
P
16
7
7
A
=
1
-
1
A
1
1
1
N
=
5
-
1
N
14
5
5
G
=
7
-
1
G
7
7
7
R
=
9
-
1
R
18
9
9
A
=
1
-
1
A
1
1
1
M
=
4
-
1
M
13
4
4
-
-
34
-
7
PANGRAM
70
34
34
-
-
3+4
-
-
-
7+0
3+4
3+4
-
-
7
-
7
PANGRAM
9
7
7

 

What sentence contains all the letters of the alphabet?

Everybody knows one or two pangrams (sentences that use every letter of the alphabet). You've probably seen some of these before: The quick brown fox jumps over a lazy dog. Pack my box with five dozen liquor jugs.

 


Big on the Internet
Sentences That Contain Every Letter of the Alphabet
by Robert Quigley (  ) | Thursday, August 5th 2010 at 4:23 pm

A pangram, or holoalphabetic sentence, is a sentence that contains every letter of the alphabet at least once. The most famous pangram is probably the thirty-five-letter-long “The quick brown fox jumps over the lazy dog,” which has been used to test typing equipment since at least the late 1800s.

Pangrams are an important tool for testing typing equipment and compactly showing off every letter of a typeface; trying to pack every letter into as short a sentence as possible is also a sort of sport among linguists and puzzle-solvers.

Here are a few that are famous or otherwise cool:

● “Sphinx of black quartz, judge my vow”: Used by Adobe InDesign to display font samples. (29 letters)

●”Jackdaws love my big sphinx of quartz”: Similarly, used by Windows XP for some fonts. (31 letters)

●”Pack my box with five dozen liquor jugs”: According to Wikipedia, this one is used on NASA’s Space Shuttle. (32 letters)

●”The quick onyx goblin jumps over the lazy dwarf”: Flavor text from an Unhinged Magic Card. (39 letters)

●”Cwm fjord bank glyphs vext quiz”: Amazingly, this 26-word-long sentence uses every letter only once, though it uses some pretty archaic words; translates to “Carved symbols in a mountain hollow on the bank of an inlet irritated an eccentric person.”

●”How razorback-jumping frogs can level six piqued gymnasts!”: Not going to win any brevity awards at 49 letters long, but old-time Mac users may recognize it.

●”Cozy lummox gives smart squid who asks for job pen”: A 41-letter tester sentence for Mac computers after System 7.

A few others we like: “Amazingly few discotheques provide jukeboxes”; “‘Now fax quiz Jack!’ my brave ghost pled”; “Watch Jeopardy!, Alex Trebek’s fun TV quiz game.”

(via Wikipedia; title image via woot.)

 

 

Pangram - Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Pangram

... pangram. An example is the phrase "Cwm fjord bank glyphs vext quiz" (cwm, a loan word from Welsh, means a steep-sided valley, particularly in Wales).

Pangram

From Wikipedia, the free encyclopedia

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. (September 2013)

English language pangram in Baskerville font.
A Pangram (Greek: παν γράμμα, pan gramma, "every letter") or holoalphabetic sentence for a given alphabet is a sentence using every letter of the alphabet at least once. Pangrams have been used to display typefaces, test equipment, and develop skills in handwriting, calligraphy, and keyboarding.

The best known English pangram is "The quick brown fox jumps over the lazy dog." It has been used since at least the late 19th century, was utilized by Western Union to test Telex / TWX data communication equipment for accuracy and reliability, and is now used by a number of computer programs (most notably the font viewer built into Microsoft Windows) to display computer fonts.

An example in another language is the German Victor jagt zwölf Boxkämpfer quer über den großen Sylter Deich, containing all letters used in German, including every umlaut (ä, ö, ü) plus the ß. It has been used since before 1800.

Short pangrams in English are more difficult to come up with and tend to use uncommon words, because the English language uses some letters (especially vowels) much more frequently than others. Longer pangrams may afford more opportunity for humor, cleverness, or thoughtfulness.[1] In a sense, the pangram is the opposite of the lipogram, in which the aim is to omit one or more letters. A perfect pangram contains every letter of the alphabet only once and can be considered an anagram of the alphabet; it is the shortest possible pangram. An example is the phrase "Cwm fjord bank glyphs vext quiz" (cwm, a loan word from Welsh, means a steep-sided valley, particularly in Wales).

 

Contents [hide]
1 Logographic scripts
2 Self-enumerating pangrams
3 Pangrams in literature
4 See also 4.1 Pangram lists

5 References

Logographic scripts[edit]

Logographic scripts, that is, writing systems composed principally of logograms, cannot be used to produce pangrams in the literal sense, since they are radically different from alphabets or other phonetic writing systems. In such scripts, the total number of signs is large and imprecisely defined, so producing a text with every possible sign is impossible. However, various analogies to pangrams are feasible, including traditional pangrams in a romanization. In Japanese, although typical orthography uses kanji (logograms), pangrams are instead required to contain every kana (syllabic character) when written out in kana alone: the Iroha is a classic example.

In addition, it is possible to create pangrams that demonstrate certain aspects of logographic characters.
Chinese: The Thousand Character Classic is a 1000-character poem in which each character is used exactly once, but it does not include all Chinese characters.
The single character 永 (permanence) incorporates every basic stroke used to write Chinese characters exactly once, as described in the Eight Principles of Yong.

Self-enumerating pangrams[edit]

A self-enumerating pangram is a pangrammatic autogram, or a sentence that inventories its own letters, each of which occurs at least once. The first ever example was produced by Rudy Kousbroek, a Dutch journalist and essayist, who publicly challenged Lee Sallows, a British recreational mathematician resident in the Netherlands, to produce an English translation of his Dutch pangram. In the sequel, Sallows built an electronic "pangram machine", that performed a systematic search among millions of candidate solutions. The machine was successful in identifying the following 'magic' translation:[2][3][4]
This pangram contains four As, one B, two Cs, one D, thirty Es, six Fs, five Gs, seven Hs, eleven Is, one J, one K, two Ls, two Ms, eighteen Ns, fifteen Os, two Ps, one Q, five Rs, twenty-seven Ss, eighteen Ts, two Us, seven Vs, eight Ws, two Xs, three Ys, & one Z.
Other approaches have been taken to find self-enumerating pangrams, too. Chris Patuzzo, a British computer scientist was able to reduce the problem of finding a self-enumerating pangram to the Boolean satisfiability problem. He did this by using a bespoke Hardware description language as a stepping stone and then applied the Tseitin transformation to the resulting chip.[5]

Pangrams in literature[edit]

Pangram "The quick brown fox..." and searches of a shorter pangram are the cornerstone of a plot of the novel by Mark Dunn "Ella Minnow Pea".[6] Search successfully comes to the end with finding "Pack my box with five dozen liquor jugs".

 

 

HURRAH FOR RAH FOR RAH HURRAH

 

 

T
=
2
-
3
THE
33
15
6
A
=
1
-
6
ANUBIS
66
21
3
-
-
3
Q
9
First Total
99
36
9
-
-
-
-
-
Add to Reduce
9+9
3+6
-
-
-
3
-
9
Second Total
18
9
9
-
-
-
-
-
Reduce to Deduce
1+8
-
-
-
-
3
-
9
Essence of Number
9
9
9

 

 

www.merriam-webster.com/dictionary/algorithm

a procedure for solving a mathematical problem (as of finding the greatest common divisor) in a finite number of steps that frequently involves repetition of an ...

algorithm [ˈælgəˌrɪðəm]
n
1. (Mathematics) a logical arithmetical or computational procedure that if correctly applied ensures the solution of a problem Compare heuristic
2. (Mathematics) Logic Maths a recursive procedure whereby an infinite sequence of terms can be generated Also called algorism
[changed from algorism, through influence of Greek arithmos number]
algorithmic adj
aal·go·rithm (lg-rm)
n.
A step-by-step problem-solving procedure, especially an established, recursive computational procedure for solving a problem in a finite number of steps.
algorithmically adv

algorithm (lg-rthm)
A finite set of unambiguous instructions performed in a prescribed sequence to achieve a goal, especially a mathematical rule or procedure used to compute a desired result. Algorithms are the basis for most computer programming.

Noun 1. algorithm - a precise rule (or set of rules) specifying how to solve some problem
algorithmic program, algorithmic rule
formula, rule - (mathematics) a standard procedure for solving a class of mathematical problems; "he determined the upper bound with Descartes' rule of signs"; "he gave us a general formula for attacking polynomials"
sorting algorithm - an algorithm for sorting a list
stemming algorithm, stemmer - an algorithm for removing inflectional and derivational endings in order to reduce word forms to a common stem algorithm
any methodology for solving a certain kind of problem.
See also: Mathematics

 

 

Algorithm
From Wikipedia, the free encyclopedia

Flow chart of an algorithm (Euclid's algorithm) for calculating the greatest common divisor (g.c.d.) of two numbers a and b in locations named A and B. The algorithm proceeds by successive subtractions in two loops: IF the test B ≥ A yields "yes" (or true) (more accurately the number b in location B is greater than or equal to the number a in location A) THEN, the algorithm specifies B ← B − A (meaning the number b − a replaces the old b). Similarly, IF A > B, THEN A ← A − B. The process terminates when (the contents of) B is 0, yielding the g.c.d. in A. (Algorithm derived from Scott 2009:13; symbols and drawing style from Tausworthe 1977).
In mathematics and computer science, an algorithm (i/ˈælɡərɪðəm/) is a step-by-step procedure for calculations. Algorithms are used for calculation, data processing, and automated reasoning.

More precisely, an algorithm is an effective method expressed as a finite list[1] of well-defined instructions[2] for calculating a function.[3] Starting from an initial state and initial input (perhaps empty),[4] the instructions describe a computation that, when executed, will proceed through a finite [5] number of well-defined successive states, eventually producing "output"[6] and terminating at a final ending state. The transition from one state to the next is not necessarily deterministic; some algorithms, known as randomized algorithms, incorporate random input.[7]

Though al-Khwārizmī's algorism referred to the rules of performing arithmetic using Hindu-Arabic numerals and the systematic solution of linear and quadratic equations, a partial formalization of what would become the modern algorithm began with attempts to solve the Entscheidungsproblem (the "decision problem") posed by David Hilbert in 1928. Subsequent formalizations were framed as attempts to define "effective calculability"[8] or "effective method";[9] those formalizations included the Gödel–Herbrand–Kleene recursive functions of 1930, 1934 and 1935, Alonzo Church's lambda calculus of 1936, Emil Post's "Formulation 1" of 1936, and Alan Turing's Turing machines of 1936–7 and 1939. Giving a formal definition of algorithms, corresponding to the intuitive notion, remains a challenging problem.[10]

Informal definition
For a detailed presentation of the various points of view around the definition of "algorithm" see Algorithm characterizations. For examples of simple addition algorithms specified in the detailed manner described in Algorithm characterizations, see Algorithm examples.
While there is no generally accepted formal definition of "algorithm," an informal definition could be "a set of rules that precisely defines a sequence of operations."[11] For some people, a program is only an algorithm if it stops eventually; for others, a program is only an algorithm if it stops before a given number of calculation steps.[12]

A prototypical example of an algorithm is Euclid's algorithm to determine the maximum common divisor of two integers; an example (there are others) is described by the flow chart above and as an example in a later section.

Boolos & Jeffrey (1974, 1999) offer an informal meaning of the word in the following quotation:

No human being can write fast enough, or long enough, or small enough† ( †"smaller and smaller without limit ...you'd be trying to write on molecules, on atoms, on electrons") to list all members of an enumerably infinite set by writing out their names, one after another, in some notation. But humans can do something equally useful, in the case of certain enumerably infinite sets: They can give explicit instructions for determining the nth member of the set, for arbitrary finite n. Such instructions are to be given quite explicitly, in a form in which they could be followed by a computing machine, or by a human who is capable of carrying out only very elementary operations on symbols.[13]

The term "enumerably infinite" means "countable using integers perhaps extending to infinity." Thus, Boolos and Jeffrey are saying that an algorithm implies instructions for a process that "creates" output integers from an arbitrary "input" integer or integers that, in theory, can be chosen from 0 to infinity. Thus an algorithm can be an algebraic equation such as y = m + n—two arbitrary "input variables" m and n that produce an output y. But various authors' attempts to define the notion indicate that the word implies much more than this, something on the order of (for the addition example):
Precise instructions (in language understood by "the computer")[14] for a fast, efficient, "good"[15] process that specifies the "moves" of "the computer" (machine or human, equipped with the necessary internally contained information and capabilities)[16] to find, decode, and then process arbitrary input integers/symbols m and n, symbols + and = ... and "effectively"[17] produce, in a "reasonable" time,[18] output-integer y at a specified place and in a specified format.
The concept of algorithm is also used to define the notion of decidability. That notion is central for explaining how formal systems come into being starting from a small set of axioms and rules. In logic, the time that an algorithm requires to complete cannot be measured, as it is not apparently related with our customary physical dimension. From such uncertainties, that characterize ongoing work, stems the unavailability of a definition of algorithm that suits both concrete (in some sense) and abstract usage of the term.

[edit] Formalization

Algorithms are essential to the way computers process data. Many computer programs contain algorithms that detail the specific instructions a computer should perform (in a specific order) to carry out a specified task, such as calculating employees' paychecks or printing students' report cards. Thus, an algorithm can be considered to be any sequence of operations that can be simulated by a Turing-complete system. Authors who assert this thesis include Minsky (1967), Savage (1987) and Gurevich (2000):

Minsky: "But we will also maintain, with Turing . . . that any procedure which could "naturally" be called effective, can in fact be realized by a (simple) machine. Although this may seem extreme, the arguments . . . in its favor are hard to refute".[19]

Gurevich: "...Turing's informal argument in favor of his thesis justifies a stronger thesis: every algorithm can be simulated by a Turing machine ... according to Savage [1987], an algorithm is a computational process defined by a Turing machine".[20]

Typically, when an algorithm is associated with processing information, data is read from an input source, written to an output device, and/or stored for further processing. Stored data is regarded as part of the internal state of the entity performing the algorithm. In practice, the state is stored in one or more data structures.

For some such computational process, the algorithm must be rigorously defined: specified in the way it applies in all possible circumstances that could arise. That is, any conditional steps must be systematically dealt with, case-by-case; the criteria for each case must be clear (and computable).

Because an algorithm is a precise list of precise steps, the order of computation will always be critical to the functioning of the algorithm. Instructions are usually assumed to be listed explicitly, and are described as starting "from the top" and going "down to the bottom", an idea that is described more formally by flow of control.

So far, this discussion of the formalization of an algorithm has assumed the premises of imperative programming. This is the most common conception, and it attempts to describe a task in discrete, "mechanical" means. Unique to this conception of formalized algorithms is the assignment operation, setting the value of a variable. It derives from the intuition of "memory" as a scratchpad. There is an example below of such an assignment.

For some alternate conceptions of what constitutes an algorithm see functional programming and logic programming.

[edit] Expressing algorithms

Algorithms can be expressed in many kinds of notation, including natural languages, pseudocode, flowcharts, programming languages or control tables (processed by interpreters). Natural language expressions of algorithms tend to be verbose and ambiguous, and are rarely used for complex or technical algorithms. Pseudocode, flowcharts and control tables are structured ways to express algorithms that avoid many of the ambiguities common in natural language statements. Programming languages are primarily intended for expressing algorithms in a form that can be executed by a computer, but are often used as a way to define or document algorithms.

There is a wide variety of representations possible and one can express a given Turing machine program as a sequence of machine tables (see more at finite state machine, state transition table and control table), as flowcharts (see more at state diagram), or as a form of rudimentary machine code or assembly code called "sets of quadruples" (see more at Turing machine).

Representations of algorithms can be classed into three accepted levels of Turing machine description:[21]
1 High-level description:
"...prose to describe an algorithm, ignoring the implementation details. At this level we do not need to mention how the machine manages its tape or head." 2 Implementation description:
"...prose used to define the way the Turing machine uses its head and the way that it stores data on its tape. At this level we do not give details of states or transition function." 3 Formal description:
Most detailed, "lowest level", gives the Turing machine's "state table". For an example of the simple algorithm "Add m+n" described in all three levels see Algorithm examples.
[edit] Implementation

Most algorithms are intended to be implemented as computer programs. However, algorithms are also implemented by other means, such as in a biological neural network (for example, the human brain implementing arithmetic or an insect looking for food), in an electrical circuit, or in a mechanical device.

[edit] Computer algorithms

Flowchart examples of the canonical Böhm-Jacopini structures: the SEQUENCE (rectangles descending the page), the WHILE-DO and the IF-THEN-ELSE. The three structures are made of the primitive conditional GOTO (IF test=true THEN GOTO step xxx) (a diamond), the unconditional GOTO (rectangle), various assignment operators (rectangle), and HALT (rectangle). Nesting of these structures inside assignment-blocks result in complex diagrams (cf Tausworthe 1977:100,114).
In computer systems, an algorithm is basically an instance of logic written in software by software developers to be effective for the intended "target" computer(s), in order for the target machines to produce output from given input (perhaps null).

"Elegant" (compact) programs, "good" (fast) programs : The notion of "simplicity and elegance" appears informally in Knuth and precisely in Chaitin:
Knuth: ". . .we want good algorithms in some loosely defined aesthetic sense. One criterion . . . is the length of time taken to perform the algorithm . . .. Other criteria are adaptability of the algorithm to computers, its simplicity and elegance, etc"[22] Chaitin: " . . . a program is 'elegant,' by which I mean that it's the smallest possible program for producing the output that it does"[23]
Chaitin prefaces his definition with: "I'll show you can't prove that a program is 'elegant'"—such a proof would solve the Halting problem (ibid).

Algorithm versus function computable by an algorithm: For a given function multiple algorithms may exist. This will be true, even without expanding the available instruction set available to the programmer. Rogers observes that "It is . . . important to distinguish between the notion of algorithm, i.e. procedure and the notion of function computable by algorithm, i.e. mapping yielded by procedure. The same function may have several different algorithms".[24]

Unfortunately there may be a tradeoff between goodness (speed) and elegance (compactness)—an elegant program may take more steps to complete a computation than one less elegant. An example of using Euclid's algorithm will be shown below.

Computers (and computors), models of computation: A computer (or human "computor"[25]) is a restricted type of machine, a "discrete deterministic mechanical device"[26] that blindly follows its instructions.[27] Melzak's and Lambek's primitive models[28] reduced this notion to four elements: (i) discrete, distinguishable locations, (ii) discrete, indistinguishable counters[29] (iii) an agent, and (iv) a list of instructions that are effective relative to the capability of the agent.[30]

Minsky describes a more congenial variation of Lambek's "abacus" model in his "Very Simple Bases for Computability".[31] Minsky's machine proceeds sequentially through its five (or six depending on how one counts) instructions unless either a conditional IF–THEN GOTO or an unconditional GOTO changes program flow out of sequence. Besides HALT, Minsky's machine includes three assignment (replacement, substitution)[32] operations: ZERO (e.g. the contents of location replaced by 0: L ← 0), SUCCESSOR (e.g. L ← L+1), and DECREMENT (e.g. L ← L − 1).[33] Rarely will a programmer have to write "code" with such a limited instruction set. But Minsky shows (as do Melzak and Lambek) that his machine is Turing complete with only four general types of instructions: conditional GOTO, unconditional GOTO, assignment/replacement/substitution, and HALT.[34]

Simulation of an algorithm: computer (computor) language: Knuth advises the reader that "the best way to learn an algorithm is to try it . . . immediately take pen and paper and work through an example".[35] But what about a simulation or execution of the real thing? The programmer must translate the algorithm into a language that the simulator/computer/computor can effectively execute. Stone gives an example of this: when computing the roots of a quadratic equation the computor must know how to take a square root. If they don't then for the algorithm to be effective it must provide a set of rules for extracting a square root.[36]

This means that the programmer must know a "language" that is effective relative to the target computing agent (computer/computor).

But what model should be used for the simulation? Van Emde Boas observes "even if we base complexity theory on abstract instead of concrete machines, arbitrariness of the choice of a model remains. It is at this point that the notion of simulation enters".[37] When speed is being measured, the instruction set matters. For example, the subprogram in Euclid's algorithm to compute the remainder would execute much faster if the programmer had a "modulus" (division) instruction available rather than just subtraction (or worse: just Minsky's "decrement").

Structured programming, canonical structures: Per the Church-Turing thesis any algorithm can be computed by a model known to be Turing complete, and per Minsky's demonstrations Turing completeness requires only four instruction types—conditional GOTO, unconditional GOTO, assignment, HALT. Kemeny and Kurtz observe that while "undisciplined" use of unconditional GOTOs and conditional IF-THEN GOTOs can result in "spaghetti code" a programmer can write structured programs using these instructions; on the other hand "it is also possible, and not too hard, to write badly structured programs in a structured language".[38] Tausworthe augments the three Böhm-Jacopini canonical structures:[39] SEQUENCE, IF-THEN-ELSE, and WHILE-DO, with two more: DO-WHILE and CASE.[40] An additional benefit of a structured program will be one that lends itself to proofs of correctness using mathematical induction.[41]

Canonical flowchart symbols[42]: The graphical aide called a flowchart offers a way to describe and document an algorithm (and a computer program of one). Like program flow of a Minsky machine, a flowchart always starts at the top of a page and proceeds down. Its primary symbols are only 4: the directed arrow showing program flow, the rectangle (SEQUENCE, GOTO), the diamond (IF-THEN-ELSE), and the dot (OR-tie). The Böhm-Jacopini canonical structures are made of these primitive shapes. Sub-structures can "nest" in rectangles but only if a single exit occurs from the superstructure. The symbols and their use to build the canonical structures are shown in the diagram.

 

 

EVOLVE LOVE EVOLVE

LOVES SOLVE LOVES

EVOLVE LOVE EVOLVE

 

 

Algorithm - Wikipedia, the free encyclopedia en.wikipedia.org/wiki/Algorithm

In mathematics and computer science, an algorithm is a step-by-step procedure for calculations. Algorithms are used for calculation, data processing, and ...

 

A
=
1
-
9
ALGORITHM
103
49
4
A
=
1
-
10
ALGORITHMS
122
59
5
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
A
=
1
-
-
ALGORITHMS
-
-
-
-
-
-
-
1
A
1
1
1
-
-
-
-
1
L
12
3
3
-
-
-
-
1
G
7
7
7
-
-
-
-
1
O
15
6
6
-
-
-
-
1
R
18
9
9
-
-
-
-
1
I
9
9
9
-
-
-
-
1
T
20
2
2
-
-
-
-
1
H
8
8
8
-
-
-
-
1
M+S
32
14
5
A
=
1
-
10
ALGORITHMS
122
59
50
-
-
-
-
1+0
-
1+2+2
5+9
5+0
A
=
1
-
1
ALGORITHMS
5
14
5
-
-
-
-
-
-
-
1+4
-
A
=
1
-
1
ALGORITHMS
5
5
5

 

 

-
10
A
L
G
O
R
I
T
H
M
S
-
-
-
-
-
-
-
-
-
-
-
-
-
6
-
9
-
8
-
1
+
=
24
2+4
=
6
=
6
-
-
-
-
-
15
-
9
-
8
-
19
+
=
51
5+1
=
6
=
6
-
10
A
L
G
O
R
I
T
H
M
S
-
-
-
-
-
-
-
-
-
-
1
3
7
-
9
-
2
-
4
-
+
=
26
2+6
=
8
=
8
-
-
1
12
7
-
18
-
20
-
13
-
+
=
71
7+1
=
8
=
8
-
10
A
L
G
O
R
I
T
H
M
S
-
-
-
-
-
-
-
-
-
-
1
12
7
15
18
9
20
8
13
19
+
=
122
1+2+2
=
5
1+0
5
-
-
1
3
7
6
9
9
2
8
4
1
+
=
50
5+0
=
5
1+0
5
-
10
A
L
G
O
R
I
T
H
M
S
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
1
-
-
1
occurs
x
2
=
2
-
-
-
-
-
-
-
-
2
-
-
-
-
-
2
occurs
x
1
=
2
-
-
-
3
-
-
-
-
-
-
-
-
-
-
3
occurs
x
1
=
3
-
-
-
-
-
-
-
-
-
-
4
-
-
-
4
occurs
x
1
=
4
5
-
-
-
-
-
-
-
-
-
-
-
-
-
5
FIVE
5
-
-
-
-
-
-
-
-
6
-
-
-
-
-
-
-
-
6
occurs
x
1
=
6
-
-
-
-
7
-
-
-
-
-
-
-
-
-
7
occurs
x
1
=
7
-
-
-
-
-
-
-
-
-
8
-
-
-
-
8
occurs
x
1
=
8
-
-
-
-
-
-
9
9
-
-
-
-
-
-
9
occurs
x
1
=
9
5
10
A
L
G
O
R
I
T
H
M
S
-
-
27
-
-
10
-
41
-
1+0
-
-
-
-
9
9
-
-
-
-
-
-
2+7
-
-
1+0
-
4+1
5
1
A
L
G
O
R
I
T
H
M
S
-
-
9
-
-
1
-
5
-
-
1
3
7
6
9
9
2
8
4
1
-
-
-
-
-
-
-
-
5
1
A
L
G
O
R
I
T
H
M
S
-
-
9
-
-
1
-
5

 

 

A
=
1
-
10
ALGORITHMS
122
59
5
A
=
1
-
9
ALGORITHM
103
49
4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
ALGORITHM
-
-
-
A
=
1
-
1
A
1
1
1
L
=
3
-
1
L
12
3
3
G
=
7
-
1
G
7
7
7
O
=
6
-
1
O
15
6
6
R
=
9
-
1
R
18
9
9
I
=
9
-
1
I
9
9
9
T
=
2
-
1
T
20
2
2
H
=
8
-
1
H
8
8
8
M
=
4
-
1
M
13
4
4
-
-
49
-
9
ALGORITHM
103
49
49
-
-
4+9
-
-
-
1+0+3
4+9
4+9
-
-
13
-
9
ALGORITHM
103
13
13
-
-
1+3
-
-
-
-
1+3
1+3
-
-
4
-
9
ALGORITHM
103
4
4

 

 

A
=
1
-
10
ALGORITHMS
122
59
5
A
=
1
-
9
ALGORITHM
103
49
4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
ALGORITHM
-
-
-
A
=
1
-
1
A
1
1
1
T
=
2
-
1
T
20
2
2
L
=
3
-
1
L
12
3
3
M
=
4
-
1
M
13
4
4
5
-
5
-
-
5
-
-
5
O
=
6
-
1
O
15
6
6
G
=
7
-
1
G
7
7
7
H
=
8
-
1
H
8
8
8
R
=
9
-
1
R
18
9
9
I
=
9
-
1
I
9
9
9
-
-
49
-
9
ALGORITHM
103
49
49
-
-
4+9
-
-
-
1+0+3
4+9
4+9
-
-
13
-
9
ALGORITHM
103
13
13
-
-
1+3
-
-
-
-
1+3
1+3
-
-
4
-
9
ALGORITHM
103
4
4

 

 

A
=
1
-
10
ALGORITHMS
122
59
5
A
=
1
-
9
ALGORITHM
103
49
4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
ALGORITHM
-
-
-
A
=
1
-
1
A
1
1
1
L
=
3
-
1
L
12
3
3
G
=
7
-
1
G
7
7
7
O
=
6
-
1
O
15
6
6
R
=
9
-
1
R
18
9
9
I
=
9
-
1
I
9
9
9
T
=
2
-
1
T
20
2
2
H
=
8
-
1
H
8
8
8
M
=
4
-
1
M
13
4
4
-
-
49
-
9
ALGORITHM
103
49
49
-
-
4+9
-
-
-
1+0+3
4+9
4+9
-
-
13
-
9
ALGORITHM
103
13
13
-
-
1+3
-
-
-
-
1+3
1+3
-
-
4
-
9
ALGORITHM
103
4
4

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
ALGORITHMS
-
-
-
-
-
-
-
-
-
-
-
-
-
A
=
1
1
1
A
1
1
1
-
1
-
-
-
-
-
-
-
-
L
=
3
2
1
L
12
3
3
-
-
-
3
-
-
-
-
-
-
G
=
7
3
1
G
7
7
7
-
-
-
-
-
-
-
7
-
-
O
=
6
4
1
O
15
6
6
-
-
-
-
-
-
6
-
-
-
R
=
9
5
1
R
18
9
9
-
-
-
-
-
-
-
-
-
9
I
=
9
6
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
T
=
2
7
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
H
=
8
8
1
H
8
8
8
-
-
-
-
-
-
-
-
8
-
M
=
4
9
1
M
13
4
4
-
-
-
-
4
-
-
-
-
-
S
=
1
10
1
S
1
1
1
-
1
-
-
-
-
-
-
-
-
-
-
50
-
10
ALGORITHMS
122
50
50
-
2
2
3
4
5
6
7
8
18
-
-
5+0
-
1+0
-
1+2+2
5+5
5+0
-
-
-
-
-
-
-
-
-
1+8
-
-
5
-
1
ALGORITHMS
5
5
5
-
2
2
3
4
5
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
6
7
8
9
-
-
-
-
-
ALGORITHMS
-
-
-
-
-
-
-
-
-
-
-
-
A
=
1
1
1
A
1
1
1
-
1
-
-
-
-
-
-
-
L
=
3
2
1
L
12
3
3
-
-
-
3
-
-
-
-
-
G
=
7
3
1
G
7
7
7
-
-
-
-
-
-
7
-
-
O
=
6
4
1
O
15
6
6
-
-
-
-
-
6
-
-
-
R
=
9
5
1
R
18
9
9
-
-
-
-
-
-
-
-
9
I
=
9
6
1
I
9
9
9
-
-
-
-
-
-
-
-
9
T
=
2
7
1
T
20
2
2
-
-
2
-
-
-
-
-
-
H
=
8
8
1
H
8
8
8
-
-
-
-
-
-
-
8
-
M
=
4
9
1
M
13
4
4
-
-
-
-
4
-
-
-
-
S
=
1
10
1
S
1
1
1
-
1
-
-
-
-
-
-
-
-
-
50
-
10
ALGORITHMS
122
50
50
-
2
2
3
4
6
7
8
18
-
-
5+0
-
1+0
-
1+2+2
5+5
5+0
-
-
-
-
-
-
-
-
1+8
-
-
5
-
1
ALGORITHMS
5
5
5
-
2
2
3
4
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
ALGORITHMS
-
-
-
-
-
-
-
-
-
-
-
-
-
A
=
1
1
1
A
1
1
1
-
1
-
-
-
5
-
-
-
-
S
=
1
10
1
S
1
1
1
-
1
-
-
-
5
-
-
-
-
T
=
2
7
1
T
20
2
2
-
-
2
-
-
5
-
-
-
-
L
=
3
2
1
L
12
3
3
-
-
-
3
-
5
-
-
-
-
M
=
4
9
1
M
13
4
4
-
-
-
-
4
5
-
-
-
-
O
=
6
4
1
O
15
6
6
-
-
-
-
-
5
6
-
-
-
G
=
7
3
1
G
7
7
7
-
-
-
-
-
5
-
7
-
-
H
=
8
8
1
H
8
8
8
-
-
-
-
-
5
-
-
8
-
R
=
9
5
1
R
18
9
9
-
-
-
-
-
5
-
-
-
9
I
=
9
6
1
I
9
9
9
-
-
-
-
-
5
-
-
-
9
-
-
50
-
10
ALGORITHMS
122
50
50
-
2
2
3
4
5
6
7
8
18
-
-
5+0
-
1+0
-
1+2+2
5+5
5+0
-
-
-
-
-
-
-
-
-
1+8
-
-
5
-
1
ALGORITHMS
5
5
5
-
2
2
3
4
5
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
6
7
8
9
-
-
-
-
-
ALGORITHMS
-
-
-
-
-
-
-
-
-
-
-
-
A
=
1
1
1
A
1
1
1
-
1
-
-
-
-
-
-
-
S
=
1
10
1
S
1
1
1
-
1
-
-
-
-
-
-
-
T
=
2
7
1
T
20
2
2
-
-
2
-
-
-
-
-
-
L
=
3
2
1
L
12
3
3
-
-
-
3
-
-
-
-
-
M
=
4
9
1
M
13
4
4
-
-
-
-
4
-
-
-
-
O
=
6
4
1
O
15
6
6
-
-
-
-
-
6
-
-
-
G
=
7
3
1
G
7
7
7
-
-
-
-
-
-
7
-
-
H
=
8
8
1
H
8
8
8
-
-
-
-
-
-
-
8
-
R
=
9
5
1
R
18
9
9
-
-
-
-
-
-
-
-
9
I
=
9
6
1
I
9
9
9
-
-
-
-
-
-
-
-
9
-
-
50
-
10
ALGORITHMS
122
50
50
-
2
2
3
4
6
7
8
18
-
-
5+0
-
1+0
-
1+2+2
5+5
5+0
-
-
-
-
-
-
-
-
1+8
-
-
5
-
1
ALGORITHMS
5
5
5
-
2
2
3
4
6
7
8
9

 

 

NUMBER

9

THE SEARCH FOR THE SIGMA CODE

Cecil Balmond 1998

Preface to the New Edition

Page 5
Twelve years ago a little boy entered my imagination as he hopped across the centuries and played with numbers. I began to see how the simple architecture of our decimal system could be constructed in secret ways — not a building project this time but an abstract one. On the surface of our arithmetic countless combinations of numbers take part in tedious and exacting calculations but underneath it all there is pattern, governed by a repeating code of integers. The Sigma Code reduces numbers to a single digit and the illusion of the many is seen to be but the reflection of a few. This is not a book on maths: this is a book for anyone who can carry out simple sums in their heads, and who won't be short-changed knowingly.
When Number 9 first came out I received mail from many who played with numbers. They chased patterns; some had special numbers and even mystical systems. I was tempted to write about numerology but resisted. I wanted to write about the intricacy of what the.. numbers actually do and leave the reader to wonder about the larger irrational that seems to hover around such constructions.
If I were writing this book today the numbers would have featured in a wider context of structuring nature's patterns, and also playing the role of animator in algorithms that create unique architectural forms and shapes. I would also include my previous research into other base systems. But this book was a first step which came from a child-like urge, like playing with building blocks, to build out of our numbers — just the simple 1, 2, 3, up to number 9.

 

RESEARCH R E SEARCH ER RESEARCH

 

 

THE LIGHT IS RISING NOW RISING IS THE LIGHT

 

 

NUMBER = 534259 = 1 = 534259 NUMBER

NUMBER = 234559 NUMBER

NUMBER = 534259 = 1 = 534259 NUMBER

 

 

NUMBERS = 5342591 = 2 = 5342591 NUMBERS

SBUMNER = 1234559 = SBUMNER

NUMBERS = 5342591 = 2 = 5342591 NUMBERS

 

-
-
-
-
Q
NUMBERS
-
Q
Q
-
1
2
3
4
5
6
7
8
-
N
=
5
-
1
N
14
5
5
-
-
-
-
-
5
6
7
8
-
U
=
3
-
1
U
21
3
3
-
-
-
3
-
-
6
7
8
-
M
=
4
-
1
M
13
4
4
-
-
-
-
4
-
6
7
8
-
B
=
2
-
1
B
2
2
2
-
-
2
-
-
-
6
7
8
-
E
=
5
-
1
E
5
5
5
-
-
-
-
-
5
6
7
8
-
R
=
9
-
1
R
18
9
9
-
-
-
-
-
-
6
7
8
9
S
=
1
-
1
S
19
1
1
-
1
-
-
-
-
6
7
8
-
-
-
29
4
7
NUMBERS
92
29
29
-
1
2
3
4
10
6
7
8
9
-
-
2+9
Q
-
Q
9+2
2+9
2+9
-
-
-
-
-
1+0
-
-
-
-
Q
-
11
-
7
NUMBERS
11
11
11
-
1
2
3
4
1
6
7
8
9
-
-
1+1
Q
-
Q
1+1
1+1
1+1
-
-
-
-
-
-
-
-
-
-
Q
-
2
-
7
NUMBERS
2
2
2
-
1
2
3
4
1
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
9
-
-
-
-
Q
NUMBERS
-
Q
Q
-
-
-
-
-
-
-
N
=
5
-
1
N
14
5
5
-
-
-
-
-
5
-
U
=
3
-
1
U
21
3
3
-
-
-
3
-
-
-
M
=
4
-
1
M
13
4
4
-
-
-
-
4
-
-
B
=
2
-
1
B
2
2
2
-
-
2
-
-
-
-
E
=
5
-
1
E
5
5
5
-
-
-
-
-
5
-
R
=
9
-
1
R
18
9
9
-
-
-
-
-
-
9
S
=
1
-
1
S
19
1
1
-
1
-
-
-
-
-
-
-
29
4
7
NUMBERS
92
29
29
-
1
2
3
4
10
9
-
-
2+9
Q
-
Q
9+2
2+9
2+9
-
-
-
-
-
1+0
-
Q
-
11
-
7
NUMBERS
11
11
11
-
1
2
3
4
1
9
-
-
1+1
Q
-
Q
1+1
1+1
1+1
-
-
-
-
-
-
-
Q
-
2
-
7
NUMBERS
2
2
2
-
1
2
3
4
1
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
3
-
-
-
-
Q
NUMBERS
-
Q
Q
-
-
-
-
-
-
-
S
=
1
-
1
S
19
1
1
-
1
-
-
-
-
-
B
=
2
-
1
B
2
2
2
-
-
2
-
-
-
-
U
=
3
-
1
U
21
3
3
-
-
-
3
-
-
-
M
=
4
-
1
M
13
4
4
-
-
-
-
4
-
-
N
=
5
-
1
N
14
5
5
-
-
-
-
-
5
-
E
=
5
-
1
E
5
5
5
-
-
-
-
-
5
-
R
=
9
-
1
R
18
9
9
-
-
-
-
-
-
9
-
-
29
4
7
NUMBERS
92
29
29
-
1
2
3
4
10
9
-
-
2+9
Q
-
Q
9+2
2+9
2+9
-
-
-
-
-
1+0
-
Q
-
11
-
7
NUMBERS
11
11
11
-
1
2
3
4
1
9
-
-
1+1
Q
-
Q
1+1
1+1
1+1
-
-
-
-
-
-
-
Q
-
2
-
7
NUMBERS
2
2
2
-
1
2
3
4
1
9

 

 

I = 9 9 = I
ME = 9 9 = ME
BRAIN + BODY = 9 9 = BODY + BRAIN
LIGHT + DARK = 9 9 = DARK + LIGHT
ENERGY + MASS = 9 9 = MASS +ENERGY
MIND + MATTER = 9 9 = MATTER + MIND
MAGNETIC + FIELD = 9 9 = FIELD + MAGNETIC
POSITIVE + NEGATIVE = 9 9 = NEGATIVE + POSITIVE
973 OM AZAZAZAZAZAZAZAZAZZAZAZAZAZAZAZAZAZAOM 973

 

 

-
7
A
L
G
E
B
R
A
-
-
-
-
-
-
-
-
-
-
1
3
7
5
2
9
1
+
=
28
2+8
=
10
1+0
1
-
-
1
12
7
5
2
18
1
+
=
46
4+6
=
10
1+0
1
-
7
A
L
G
E
B
R
A
-
-
-
-
-
-
-
-
-
-
1
3
7
5
2
9
1
+
=
28
2+8
=
10
1+0
1
-
-
1
12
7
5
2
18
1
+
=
46
4+6
=
10
1+0
1
-
7
A
L
G
E
B
R
A
-
-
-
-
-
-
-
-
-
-
1
12
7
5
2
18
1
+
=
46
4+6
=
10
1+0
1
-
-
1
3
7
5
2
9
1
+
=
28
2+8
=
10
1+0
1
-
7
A
L
G
E
B
R
A
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
1
-
-
1
occurs
x
2
=
2
-
-
-
-
-
-
2
-
-
-
-
2
occurs
x
1
=
2
-
-
-
3
-
-
-
-
-
-
-
3
occurs
x
1
=
3
4
-
-
-
-
-
-
-
-
-
-
4
FOUR
4
-
-
-
-
-
-
-
-
5
-
-
-
-
-
5
occurs
x
1
=
5
6
-
-
-
-
-
-
-
-
-
-
6
SIX
6
-
-
-
-
-
-
-
7
-
-
-
-
-
-
7
occurs
x
1
=
7
8
-
-
-
-
-
-
-
-
-
-
8
EIGHT
8
-
-
-
-
-
-
-
-
-
-
9
-
-
-
9
occurs
x
1
=
9
18
7
A
L
G
E
B
R
A
-
-
27
-
-
7
-
28
1+8
-
-
-
-
-
-
9
-
-
-
2+7
-
-
-
-
2+8
9
7
A
L
G
E
B
R
A
-
-
9
-
-
7
-
10
-
-
1
3
7
5
2
9
1
-
-
-
-
-
-
-
1+0
9
7
A
L
G
E
B
R
A
-
-
9
-
-
7
-
1

 

 

7
A
L
G
E
B
R
A
-
-
-
-
-
-
-
-
-
1
3
7
5
2
9
1
+
=
28
2+8
=
10
1+0
1
-
1
12
7
5
2
18
1
+
=
46
4+6
=
10
1+0
1
7
A
L
G
E
B
R
A
-
-
-
-
-
-
-
-
-
1
3
7
5
2
9
1
+
=
28
2+8
=
10
1+0
1
-
1
12
7
5
2
18
1
+
=
46
4+6
=
10
1+0
1
7
A
L
G
E
B
R
A
-
-
-
-
-
-
-
-
-
1
12
7
5
2
18
1
+
=
46
4+6
=
10
1+0
1
-
1
3
7
5
2
9
1
+
=
28
2+8
=
10
1+0
1
7
A
L
G
E
B
R
A
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
1
-
-
1
occurs
x
2
=
2
-
-
-
-
-
2
-
-
-
-
2
occurs
x
1
=
2
-
-
3
-
-
-
-
-
-
-
3
occurs
x
1
=
3
-
-
-
-
5
-
-
-
-
-
5
occurs
x
1
=
5
-
-
-
7
-
-
-
-
-
-
7
occurs
x
1
=
7
-
-
-
-
-
-
9
-
-
-
9
occurs
x
1
=
9
7
A
L
G
E
B
R
A
-
-
27
-
-
7
-
28
-
-
-
-
-
-
9
-
-
-
2+7
-
-
-
-
2+8
7
A
L
G
E
B
R
A
-
-
9
-
-
7
-
10
-
1
3
7
5
2
9
1
-
-
-
-
-
-
-
1+0
7
A
L
G
E
B
R
A
-
-
9
-
-
7
-
1

 

 

REAL REALITY REVEALED HAVE I MENTIONED GODS DIVINE THOUGHT HAVE I MENTIONED

THAT

9 9 9 9 9 9 9 9 9 9 9 9

4

 

 

-
REAL
-
-
-
1
R
18
9
9
3
E+A+L
18
9
9
4
REAL
36
18
18
-
-
3+6
1+8
1+8
4
REAL
9
9
9

 

 

-
REALITY
-
-
-
1
R
18
9
9
3
E+A+L
18
9
9
1
I
9
9
9
2
T+Y
45
9
9
7
REALITY
90
36
36
-
-
9+0
3+6
3+6
7
REALITY
9
9
9

 

 

-
REVEALED
-
-
-
1
R
18
9
9
2
E+V
27
9
9
3
E+A+L
18
9
9
2
E+D
9
9
9
8
REVEALED
72
36
36
-
-
7+2
3+6
3+6
8
REVEALED
9
9
9

 

 

-
REAL
-
-
-
1
R
18
9
9
3
E+A+L
18
9
9
-
REALITY
-
-
-
1
R
18
9
9
3
E+A+L
18
9
9
1
I
9
9
9
2
T+Y
45
9
9
12
REVEALED
-
-
-
1
R
18
9
9
2
E+V
27
9
9
3
E+A+L
18
9
9
2
E+D
9
9
9
19
First Total
198
90
36
1+9
Add to Reduce
1+9+8
9+0
3+6
10
Second Total
18
9
9
1+0
Reduce to Deduce
1+8
-
-
1
Essence of Number
9
9
9

 

 

-
4
R
E
A
L
-
-
-
-
-
--
-
-
`-
`-
-
-
-
-
+
=
-
-
-
-
-
-
-
-
-
-
-
--
+
=
-
-
-
-
-
--
-
4
R
E
A
L
-
-
-
-
-
--
-
-
-
-
9
5
1
3
+
=
18
1+8
=
9
-
9
`-
`-
18
5
1
12
+
=
36
3+6
=
9
-
9
-
4
R
E
A
L
-
-
-
-
-
--
-
-
`-
`-
18
5
1
12
+
=
36
3+6
=
9
-
9
-
-
9
5
1
3
+
=
18
1+8
=
9
-
9
-
4
R
E
A
L
-
-
-
-
-
-
-
-
-
-
-
-
1
-
--
-
1
occurs
x
1
=
1
2
-
-
-
-
-
-
-
2
TWO
2
-
-
-
-
-
-
-
-
3
-
-
3
occurs
x
1
=
3
4
-
-
-
-
-
-
-
4
FOUR
4
-
-
-
-
--
-
5
-
-
-
-
5
occurs
x
1
=
5
6
-
-
-
-
-
--
-
6
SIX
6
-
-
-
7
-
-
-
-
-
-
-
7
SEVEN
6
-
-
-
8
-
-
-
-
-
--
-
8
EIGHT
6
-
-
-
-
-
9
-
-
-
-
-
9
occurs
x
1
=
9
27
4
R
E
A
L
-
-
18
-
1
4
-
18
2+7
-
9
-
-
-
-
-
1+8
-
-
-
-
1+8
9
4
R
E
A
L
-
-
9
-
-
4
-
9
-
-
9
5
1
3
-
-
-
-
-
-
-
-
9
4
R
E
A
L
-
-
9
-
-
4
-
9

 

 

4
R
E
A
L
-
-
-
-
-
--
-
-
`-
-
-
-
-
+
=
-
-
-
-
-
-
-
-
-
-
--
+
=
-
-
-
-
-
--
4
R
E
A
L
-
-
-
-
-
--
-
-
-
9
5
1
3
+
=
18
1+8
=
9
-
9
`-
18
5
1
12
+
=
36
3+6
=
9
-
9
4
R
E
A
L
-
-
-
-
-
--
-
-
`-
18
5
1
12
+
=
36
3+6
=
9
-
9
-
9
5
1
3
+
=
18
1+8
=
9
-
9
4
R
E
A
L
-
-
-
-
-
-
-
-
-
-
-
1
-
--
-
1
occurs
x
1
=
1
-
-
-
-
3
-
-
3
occurs
x
1
=
3
--
-
5
-
-
-
-
5
occurs
x
1
=
5
-
9
-
-
-
-
-
9
occurs
x
1
=
9
4
R
E
A
L
-
-
18
-
1
4
-
18
-
9
-
-
-
-
-
1+8
-
-
-
-
1+8
4
R
E
A
L
-
-
9
-
-
4
-
9
-
9
5
1
3
-
-
-
-
-
-
-
-
4
R
E
A
L
-
-
9
-
-
4
-
9

 

 

-
7
R
E
A
L
I
T
Y
-
-
-
-
-
--
-
-
-
-
`-
`-
-
-
-
-
9
-
-
+
=
9
-
=
9
-
9
-
9
`-
`-
-
-
-
-
9
-
-
+
=
9
-
=
9
-
9
-
9
-
7
R
E
A
L
I
T
Y
-
-
-
-
-
--
-
-
-
-
-
-
9
5
1
3
-
2
7
+
=
27
2+7
=
9
-
9
-
9
`-
`-
18
5
1
12
-
20
25
+
=
81
8+1
=
9
-
9
-
9
-
7
R
E
A
L
I
T
Y
-
-
-
-
-
--
-
-
-
-
`-
`-
18
5
1
12
9
20
25
+
=
90
9+0
=
9
-
9
-
9
-
-
9
5
1
3
9
2
7
+
=
36
3+6
=
9
-
9
-
9
-
7
R
E
A
L
I
T
Y
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
1
occurs
x
1
=
1
=
1
-
-
-
-
-
-
-
2
-
-
-
2
occurs
x
1
=
2
=
2
-
-
-
-
-
3
-
-
-
--
-
3
occurs
x
1
=
3
=
3
4
-
-
-
-
-
-
-
-
-
-
4
FOUR
4
-
-
-
-
-
--
--
-
5
-
-
-
-
-
-
-
5
occurs
x
1
=
5
=
5
6
-
-
-
-
-
-
-
-
-
-
6
SIX
6
-
-
-
-
-
--
--
-
-
-
-
-
-
7
-
-
7
occurs
x
1
=
7
=
7
8
-
-
-
-
-
-
-
-
-
-
8
EIGHT
8
-
-
-
-
-
-
-
9
-
-
-
9
-
-
-
-
9
occurs
x
2
=
18
1+8
9
18
7
R
E
A
L
I
T
Y
--
-
27
-
1
7
-
36
-
27
1+8
-
9
-
-
-
9
-
-
--
-
2+7
-
-
-
-
3+6
-
2+7
9
7
R
E
A
L
I
T
Y
-
-
9
-
-
7
-
9
-
9
-
-
9
5
1
3
9
2
7
-
-
-
-
-
-
-
-
-
-
9
7
R
E
A
L
I
T
Y
-
-
9
-
-
7
-
9
-
9

 

 

7
R
E
A
L
I
T
Y
-
-
-
-
-
--
-
-
-
-
`-
-
-
-
-
9
-
-
+
=
9
-
=
9
-
9
-
9
`-
-
-
-
-
9
-
-
+
=
9
-
=
9
-
9
-
9
7
R
E
A
L
I
T
Y
-
-
-
-
-
--
-
-
-
-
-
9
5
1
3
-
2
7
+
=
27
2+7
=
9
-
9
-
9
`-
18
5
1
12
-
20
25
+
=
81
8+1
=
9
-
9
-
9
7
R
E
A
L
I
T
Y
-
-
-
-
-
--
-
-
-
-
`-
18
5
1
12
9
20
25
+
=
90
9+0
=
9
-
9
-
9
-
9
5
1
3
9
2
7
+
=
36
3+6
=
9
-
9
-
9
7
R
E
A
L
I
T
Y
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
1
occurs
x
1
=
1
=
1
-
-
-
-
-
-
2
-
-
-
2
occurs
x
1
=
2
=
2
-
-
-
-
3
-
-
-
--
-
3
occurs
x
1
=
3
=
3
--
-
5
-
-
-
-
-
-
-
5
occurs
x
1
=
5
=
5
--
-
-
-
-
-
-
7
-
-
7
occurs
x
1
=
7
=
7
-
9
-
-
-
9
-
-
-
-
9
occurs
x
2
=
18
1+8
9
7
R
E
A
L
I
T
Y
--
-
27
-
1
7
-
36
-
27
-
9
-
-
-
9
-
-
--
-
2+7
-
-
-
-
3+6
-
2+7
7
R
E
A
L
I
T
Y
-
-
9
-
-
7
-
9
-
9
-
9
5
1
3
9
2
7
-
-
-
-
-
-
-
-
-
-
7
R
E
A
L
I
T
Y
-
-
9
-
-
7
-
9
-
9

 

 

-
11
R
E
A
L
-
R
E
A
L
I
T
Y
-
-
-
-
-
--
-
-
-
-
-
`-
-
-
-
-
-
-
-
-
-
9
-
-
+
=
9
-
-
9
-
9
-
9
-
`-
-
-
-
-
-
-
-
-
-
9
-
-
+
=
9
-
-
9
-
9
-
9
-
`-
R
E
A
L
-
R
E
A
L
I
T
Y
-
-
-
-
-
--
-
-
-
-
-
11
18
5
1
12
-
18
5
1
12
-
20
25
+
=
45
4+5
=
9
-
9
-
9
-
-
9
5
1
3
-
9
5
1
3
-
2
7
+
=
117
1+1+7
=
9
=
9
-
9
-
`-
R
E
A
L
-
R
E
A
L
I
T
Y
-
-
-
-
-
--
-
-
-
-
-
11
18
5
1
12
-
18
5
1
12
9
20
25
+
=
126
1+2+6
=
9
=
9
-
9
-
`-
9
5
1
3
-
9
5
1
3
9
2
7
+
=
54
5+4
=
9
-
9
-
9
-
-
R
E
A
L
-
R
E
A
L
I
T
Y
-
-
-
-
-
--
-
-
-
-
-
11
-
-
1
-
-
-
-
1
-
-
1
-
-
-
1
occurs
x
2
=
2
=
2
-
-
-
-
-
-
-
-
-
-
-
-
2
-
-
-
2
occurs
x
1
=
2
=
2
-
-
-
-
4
3
-
-
-
4
3
-
-
-
-
-
3
occurs
x
2
=
6
=
6
4
-
-
-
4
-
-
-
-
4
-
-
-
-
-
-
4
FOUR
4
-
-
-
-
-
-
-
-
5
-
5
-
-
5
-
5
-
-
-
-
-
5
occurs
x
2
=
10
1+0
1
6
-
-
-
4
-
-
-
-
4
-
-
-
-
-
-
6
SIX
6
-
-
-
-
-
-
-
-
-
4
-
-
-
-
4
-
-
-
7
-
-
7
occurs
x
1
=
7
=
7
8
-
-
-
4
-
-
-
-
4
-
-
-
-
-
-
8
EIGHT
8
-
-
-
-
-
-
-
9
-
-
9
-
9
-
-
9
9
-
-
-
-
9
occurs
x
3
=
27
2+7
9
18
11
R
E
A
L
-
R
E
A
L
I
T
Y
-
-
27
-
-
11
-
54
-
27
1+8
1+1
9
-
-
9
-
9
-
-
9
9
-
-
-
-
2+7
-
-
1+1
-
5+4
-
2+7
9
2
R
E
A
L
-
R
E
A
L
I
T
Y
-
-
9
-
-
2
-
9
-
9
-
`-
9
5
1
3
-
9
5
1
3
9
2
7
-
-
-
-
-
--
-
-
-
-
9
2
R
E
A
L
-
R
E
A
L
I
T
Y
-
-
9
-
-
2
-
9
-
9

 

 

11
R
E
A
L
-
R
E
A
L
I
T
Y
-
-
-
-
-
--
-
-
-
-
`-
-
-
-
-
-
-
-
-
-
9
-
-
+
=
9
-
-
9
-
9
-
9
`-
-
-
-
-
-
-
-
-
-
9
-
-
+
=
9
-
-
9
-
9
-
9
`-
R
E
A
L
-
R
E
A
L
I
T
Y
-
-
-
-
-
--
-
-
-
-
11
18
5
1
12
-
18
5
1
12
-
20
25
+
=
45
4+5
=
9
-
9
-
9
-
9
5
1
3
-
9
5
1
3
-
2
7
+
=
117
1+1+7
=
9
=
9
-
9
`-
R
E
A
L
-
R
E
A
L
I
T
Y
-
-
-
-
-
--
-
-
-
-
11
18
5
1
12
-
18
5
1
12
9
20
25
+
=
126
1+2+6
=
9
=
9
-
9
`-
9
5
1
3
-
9
5
1
3
9
2
7
+
=
54
5+4
=
9
-
9
-
9
-
R
E
A
L
-
R
E
A
L
I
T
Y
-
-
-
-
-
--
-
-
-
-
11
-
-
1
-
-
-
-
1
-
-
1
-
-
-
1
occurs
x
2
=
2
=
2
-
-
-
-
-
-
-
-
-
-
-
2
-
-
-
2
occurs
x
1
=
2
=
2
-
-
-
4
3
-
-
-
4
3
-
-
-
-
-
3
occurs
x
2
=
6
=
6
-
-
5
-
5
-
-
5
-
5
-
-
-
-
-
5
occurs
x
2
=
10
1+0
1
-
-
-
4
-
-
-
-
4
-
-
-
7
-
-
7
occurs
x
1
=
7
=
7
-
9
-
-
9
-
9
-
-
9
9
-
-
-
-
9
occurs
x
3
=
27
2+7
9
11
R
E
A
L
-
R
E
A
L
I
T
Y
-
-
27
-
-
11
-
54
-
27
1+1
9
-
-
9
-
9
-
-
9
9
-
-
-
-
2+7
-
-
1+1
-
5+4
-
2+7
2
R
E
A
L
-
R
E
A
L
I
T
Y
-
-
9
-
-
2
-
9
-
9
`-
9
5
1
3
-
9
5
1
3
9
2
7
-
-
-
-
-
--
-
-
-
-
2
R
E
A
L
-
R
E
A
L
I
T
Y
-
-
9
-
-
2
-
9
-
9

 

 

4
REAL
36
18
9
7
REALITY
90
36
9
8
REVEALED
72
36
9
19
First Total
198
90
27
1+9
Add to Reduce
1+9+8
9+0
2+7
10
Second Total
18
9
9
1+0
Reduce to Deduce
1+8
-
-
1
Essence of Number
9
9
9

 

 

-
-
-
-
-
REAL REALITY REVEALED
-
-
-
R
=
18
=
9
R
18
9
9
--
-
-
-
-
E+A+L
18
9
9
R
=
18
=
9
R
18
9
9
--
-
-
-
-
E+A+L
18
9
9
--
-
-
-
-
I
9
9
9
--
-
-
-
-
T+Y
45
9
9
R
=
18
=
9
R
18
9
9
--
-
-
-
-
E+V
27
9
9
-
-
-
-
-
E+A+L
18
9
9
-
-
-
-
-
E+D
9
9
9
-
-
54
-
27
REAL REALITY REVEALED
-
-
-
-
-
5+4
-
2+7
-
-
-
-
-
-
9
-
9
REAL REALITY REVEALED
-
-
-

 

 

-
19
R
E
A
L
-
R
E
A
L
I
T
Y
-
R
E
V
E
A
L
E
D
-
-
-
-
-
--
-
-
-
-
-
`-
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
-
+
+
9
-
-
9
-
9
-
9
-
`-
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
-
+
+
9
-
-
9
-
9
-
9
-
19
R
E
A
L
-
R
E
A
L
I
T
Y
-
R
E
V
E
A
L
E
D
-
-
-
-
-
--
-
-
-
-
-
`-
18
5
1
12
-
18
5
1
12
-
20
25
-
18
5
22
5
1
12
5
4
+
+
189
1+8+9
=
18
1+8
9
-
9
-
-
9
5
1
3
-
9
5
1
3
-
2
7
-
9
5
4
5
1
3
5
4
+
+
81
8+1
=
9
-
9
-
9
-
19
R
E
A
L
-
R
E
A
L
I
T
Y
-
R
E
V
E
A
L
E
D
-
-
-
-
-
--
-
-
-
-
-
`-
18
5
1
12
-
18
5
1
12
9
20
25
-
18
5
22
5
1
12
5
4
+
+
198
1+9+8
=
18
1+8
9
-
9
-
-
9
5
1
3
-
9
5
1
3
9
2
7
-
9
5
4
5
1
3
5
4
+
+
90
9+0
=
9
-
9
-
9
-
19
R
E
A
L
-
R
E
A
L
I
T
Y
-
R
E
V
E
A
L
E
D
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
1
-
-
1
-
-
-
-
1
-
1
1
-
-
-
-
1
occurs
x
3
=
3
=
3
-
-
-
-
-
-
-
-
-
-
-
-
2
-
-
-
-
-
-
-
-
-
-
-
-
2
occurs
x
1
=
2
=
2
-
-
-
-
4
3
-
-
-
4
3
-
-
-
-
-
-
4
-
-
3
-
-
-
-
3
occurs
x
3
=
9
=
9
-
-
-
-
4
-
-
-
-
4
-
-
-
-
-
-
-
4
-
-
-
-
4
-
-
4
occurs
x
2
=
8
=
8
-
-
-
5
-
5
-
-
5
-
5
-
-
-
-
-
5
-
5
-
-
5
-
-
-
5
occurs
x
5
=
25
=
7
6
-
-
-
4
-
-
-
-
4
-
-
-
-
-
-
-
4
-
-
-
-
-
-
-
6
SIX
6
-
-
-
-
-
-
-
-
-
4
-
-
-
-
4
-
-
-
7
-
-
-
4
-
-
-
-
-
-
-
7
occurs
x
1
=
7
=
7
8
-
-
-
4
-
-
-
-
4
-
-
-
-
-
-
-
4
-
-
-
-
-
-
-
8
EIGHT
8
-
-
-
-
-
-
-
9
-
-
9
-
9
-
-
9
9
-
-
-
9
-
-
-
-
-
-
-
-
-
9
occurs
x
4
=
36
=
9
14
19
R
E
A
L
-
R
E
A
L
I
T
Y
-
R
E
V
E
A
L
E
D
-
-
31
-
-
19
-
90
-
45
1+4
1+9
-
5
-
5
-
-
5
-
5
-
-
-
-
-
5
-
5
-
-
5
-
-
-
3+1
-
-
-
-
9+0
-
4+5
5
10
R
E
A
L
-
R
E
A
L
I
T
Y
-
R
E
V
E
A
L
E
D
-
-
4
-
-
1
-
9
-
9
-
1+0
9
5
1
3
-
9
5
1
3
9
2
7
-
9
5
4
5
1
3
5
4
-
-
-
-
-
-
-
-
-
-
5
1
R
E
A
L
-
R
E
A
L
I
T
Y
-
R
E
V
E
A
L
E
D
-
-
4
-
-
1
-
9
-
9

 

 

19
R
E
A
L
-
R
E
A
L
I
T
Y
-
R
E
V
E
A
L
E
D
-
-
-
-
-
--
-
-
-
-
`-
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
-
+
+
9
-
-
9
-
9
-
9
`-
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
-
+
+
9
-
-
9
-
9
-
9
19
R
E
A
L
-
R
E
A
L
I
T
Y
-
R
E
V
E
A
L
E
D
-
-
-
-
-
--
-
-
-
-
`-
18
5
1
12
-
18
5
1
12
-
20
25
-
18
5
22
5
1
12
5
4
+
+
189
1+8+9
=
18
1+8
9
-
9
-
9
5
1
3
-
9
5
1
3
-
2
7
-
9
5
4
5
1
3
5
4
+
+
81
8+1
=
9
-
9
-
9
19
R
E
A
L
-
R
E
A
L
I
T
Y
-
R
E
V
E
A
L
E
D
-
-
-
-
-
--
-
-
-
-
`-
18
5
1
12
-
18
5
1
12
9
20
25
-
18
5
22
5
1
12
5
4
+
+
198
1+9+8
=
18
1+8
9
-
9
-
9
5
1
3
-
9
5
1
3
9
2
7
-
9
5
4
5
1
3
5
4
+
+
90
9+0
=
9
-
9
-
9
19
R
E
A
L
-
R
E
A
L
I
T
Y
-
R
E
V
E
A
L
E
D
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
1
-
-
1
-
-
-
-
1
-
1
1
-
-
-
-
1
occurs
x
3
=
3
=
3
-
-
-
-
-
-
-
-
-
-
-
2
-
-
-
-
-
-
-
-
-
-
-
-
2
occurs
x
1
=
2
=
2
-
-
-
4
3
-
-
-
4
3
-
-
-
-
-
-
4
-
-
3
-
-
-
-
3
occurs
x
3
=
9
=
9
-
-
-
4
-
-
-
-
4
-
-
-
-
-
-
-
4
-
-
-
-
4
-
-
4
occurs
x
2
=
8
=
8
-
-
5
-
5
-
-
5
-
5
-
-
-
-
-
5
-
5
-
-
5
-
-
-
5
occurs
x
5
=
25
=
7
-
-
-
4
-
-
-
-
4
-
-
-
7
-
-
-
4
-
-
-
-
-
-
-
7
occurs
x
1
=
7
=
7
-
9
-
-
9
-
9
-
-
9
9
-
-
-
9
-
-
-
-
-
-
-
-
-
9
occurs
x
4
=
36
=
9
19
R
E
A
L
-
R
E
A
L
I
T
Y
-
R
E
V
E
A
L
E
D
-
-
31
-
-
19
-
90
-
45
1+9
-
5
-
5
-
-
5
-
5
-
-
-
-
-
5
-
5
-
-
5
-
-
-
3+1
-
-
-
-
9+0
-
4+5
10
R
E
A
L
-
R
E
A
L
I
T
Y
-
R
E
V
E
A
L
E
D
-
-
4
-
-
1
-
9
-
9
1+0
9
5
1
3
-
9
5
1
3
9
2
7
-
9
5
4
5
1
3
5
4
-
-
-
-
-
-
-
-
-
-
1
R
E
A
L
-
R
E
A
L
I
T
Y
-
R
E
V
E
A
L
E
D
-
-
4
-
-
1
-
9
-
9

 

 

19
R
E
A
L
R
E
A
L
I
T
Y
R
E
V
E
A
L
E
D
-
-
-
-
-
--
-
-
-
-
`-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
+
+
9
-
-
9
-
9
-
9
`-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
+
+
9
-
-
9
-
9
-
9
19
R
E
A
L
R
E
A
L
I
T
Y
R
E
V
E
A
L
E
D
-
-
-
-
-
--
-
-
-
-
`-
18
5
1
12
18
5
1
12
-
20
25
18
5
22
5
1
12
5
4
+
+
189
1+8+9
=
18
1+8
9
-
9
-
9
5
1
3
9
5
1
3
-
2
7
9
5
4
5
1
3
5
4
+
+
81
8+1
=
9
-
9
-
9
19
R
E
A
L
R
E
A
L
I
T
Y
R
E
V
E
A
L
E
D
-
-
-
-
-
--
-
-
-
-
`-
18
5
1
12
18
5
1
12
9
20
25
18
5
22
5
1
12
5
4
+
+
198
1+9+8
=
18
1+8
9
-
9
-
9
5
1
3
9
5
1
3
9
2
7
9
5
4
5
1
3
5
4
+
+
90
9+0
=
9
-
9
-
9
19
R
E
A
L
R
E
A
L
I
T
Y
R
E
V
E
A
L
E
D
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
1
-
-
1
-
-
-
1
-
1
1
-
-
-
-
1
occurs
x
3
=
3
=
3
-
-
-
-
-
-
-
-
-
-
2
-
-
-
-
-
-
-
-
-
-
-
2
occurs
x
1
=
2
=
2
-
-
-
4
3
-
-
4
3
-
-
-
-
-
4
-
-
3
-
-
-
-
3
occurs
x
3
=
9
=
9
-
-
-
4
-
-
-
4
-
-
-
-
-
-
4
-
-
-
-
4
-
-
4
occurs
x
2
=
8
=
8
-
-
5
-
5
-
5
-
5
-
-
-
-
5
-
5
-
-
5
-
-
-
5
occurs
x
5
=
25
=
7
-
-
-
4
-
-
-
4
-
-
-
7
-
-
4
-
-
-
-
-
-
-
7
occurs
x
1
=
7
=
7
-
9
-
-
9
9
-
-
9
9
-
-
9
-
-
-
-
-
-
-
-
-
9
occurs
x
4
=
36
=
9
19
R
E
A
L
R
E
A
L
I
T
Y
R
E
V
E
A
L
E
D
-
-
31
-
-
19
-
90
-
45
1+9
-
5
-
5
-
5
-
5
-
-
-
-
5
-
5
-
-
5
-
-
-
3+1
-
-
-
-
9+0
-
4+5
10
R
E
A
L
R
E
A
L
I
T
Y
R
E
V
E
A
L
E
D
-
-
4
-
-
1
-
9
-
9
1+0
9
5
1
3
9
5
1
3
9
2
7
9
5
4
5
1
3
5
4
-
-
-
-
-
-
-
-
-
-
1
R
E
A
L
R
E
A
L
I
T
Y
R
E
V
E
A
L
E
D
-
-
4
-
-
1
-
9
-
9

 

 

REAL REALITY REVEALED HAVE I MENTIONED GODS DIVINE THOUGHT HAVE I MENTIONED

THAT

9 9 9 9 9 9 9 9 9 9 9 9

4

 

 

I

ME

THAT

HE AZIN SHE THAT IS THEE THAT IS ME

I AM THE OPPOSITE OF THE OPPOSITE I

AM THE OPPOSITE OF OPPOSITE IS THE AM

I

ALWAYS

AM

BEYOND THE VEIL ANOTHER VEIL ANOTHER VEIL BEYOND

ISISISISISISISISISISISIS 919919919919 ISISISISISISISISISISISIS

999181818181818181818 AZAZAZAZAZAZAZAZAZAZAZ818181818181818181999

122333444455555666666777777788888888999999999888888887777777666666555554444333221

999999999AUMMANIPADMEHUMAUMMANIPADMEHUMAUMMANIPADMEHUM999999999

HAIL AND HEARTY SALUTATIONS AND FRATERNAL GREETINGS SENTIENT BEINGS OF PLANET EARTH


THOUGHTS OF LOVE LIGHT AND PEACE UNTO THE ALL AND SUNDRY OF UNIVERSAL

DIVINE THOUGHT DIVINE

OUR

MESSAGE

CREATORS

LOVE EVOLVE LOVE EVOLVE LOVE

999999999999

LOVE EVOLVE LOVE EVOLVE LOVE

ADDED TO ALL MINUS NONE SHARED BY EVERYTHING MULTIPLIED IN ABUNDANCE

NAMASTE

GODS AND GODDESSES AND GODDESSES AND GODS

 

 

 

-
ROTATORS
-
-
-
1
R
18
9
9
3
O+T+A
36
9
9
4
T+O+R+S
72
18
9
8
ROTATORS
126
36
27
-
-
1+2+6
3+6
2+7
8
ROTATORS
9
9
9

 

 

-
8
R
O
T
A
T
O
R
S
-
-
-
-
-
--
-
-
-
-
-
-
-
6
-
-
-
6
-
1
+
=
13
1+3
=
4
=
4
=
4
-
-
-
15
-
-
-
15
-
19
+
=
49
4+9
=
13
1+3
4
=
4
-
8
R
O
T
A
T
O
R
S
-
-
-
-
-
--
-
-
-
-
-
-
9
-
2
1
2
-
9
-
+
=
23
2+6
=
8
=
5
=
5
-
-
18
-
20
1
20
-
18
-
+
=
77
7+7
=
14
1+4
5
=
5
-
8
R
O
T
A
T
O
R
S
-
-
-
-
-
--
-
-
-
-
-
-
18
15
20
1
20
15
18
19
+
=
126
1+2=6
=
9
=
9
=
9
-
-
9
6
2
1
2
6
9
1
+
=
36
3+6
=
9
=
9
=
9
-
8
R
O
T
A
T
O
R
S
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
1
-
-
1
occurs
x
2
=
2
=
2
-
``-
-
-
2
-
2
-
-
-
-
-
2
occurs
x
2
=
4
=
4
3
-
-
-
-
-
-
-
-
-
-
-
3
THREE
3
-
-
-
-
-
4
-
-
-
-
-
-
-
-
-
-
-
4
FOUR
4
-
-
-
-
-
5
-
-
-
-
-
-
-
-
-
-
-
5
FIVE
5
-
-
-
-
-
-
-
-
6
-
-
-
6
-
-
-
-
6
occurs
x
2
=
12
1+2
3
7
-
-
-
-
-
-
-
-
-
-
-
7
SEVEN
7
-
-
-
-
-
8
-
-
-
-
-
-
-
-
-
-
-
8
EIGHT
8
-
-
-
-
-
-
-
9
-
-
-
-
-
9
-
-
-
9
occurs
x
2
=
18
1+8
9
27
8
R
O
T
A
T
O
R
S
-
-
18
-
-
8
-
36
-
18
2+7
-
9
-``
-
-
-
-``
9
-
-
-
1+8
-
-
-
-
3+6
-
1+8
9
8
R
O
T
A
T
O
R
S
-
-
9
-
-
8
-
9
-
9
-
-
9
6
2
1
2
6
9
1
-
-
-
-
-
-
-
-
-
-
9
8
R
O
T
A
T
O
R
S
-
-
9
-
-
8
-
9
-
9

 

 

-
8
R
O
T
A
T
O
R
S
-
-
-
-
-
--
-
-
-
-
-
-
-
6
-
-
-
6
-
1
+
=
13
1+3
=
4
=
4
=
4
-
-
-
15
-
-
-
15
-
19
+
=
49
4+9
=
13
1+3
4
=
4
-
8
R
O
T
A
T
O
R
S
-
-
-
-
-
--
-
-
-
-
-
-
9
-
2
1
2
-
9
-
+
=
23
2+6
=
8
=
5
=
5
-
-
18
-
20
1
20
-
18
-
+
=
77
7+7
=
14
1+4
5
=
5
-
8
R
O
T
A
T
O
R
S
-
-
-
-
-
--
-
-
-
-
-
-
18
15
20
1
20
15
18
19
+
=
126
1+2=6
=
9
=
9
=
9
-
-
9
6
2
1
2
6
9
1
+
=
36
3+6
=
9
=
9
=
9
-
8
R
O
T
A
T
O
R
S
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
1
-
-
1
occurs
x
2
=
2
=
2
-
``-
-
-
2
-
2
-
-
-
-
-
2
occurs
x
2
=
4
=
4
3
-
-
-
-
-
-
-
-
-
-
-
3
-
3
-
-
-
-
-
4
-
-
-
-
-
-
-
-
-
-
-
4
-
4
-
-
-
-
-
5
-
-
-
-
-
-
-
-
-
-
-
5
-
5
-
-
-
-
-
-
-
-
6
-
-
-
6
-
-
-
-
6
occurs
x
2
=
12
1+2
3
7
-
-
-
-
-
-
-
-
-
-
-
7
-
7
-
-
-
-
-
8
-
-
-
-
-
-
-
-
-
-
-
8
-
8
-
-
-
-
-
-
-
9
-
-
-
-
-
9
-
-
-
9
occurs
x
2
=
18
1+8
9
27
8
R
O
T
A
T
O
R
S
-
-
18
-
-
8
-
36
-
18
2+7
-
9
-``
-
-
-
-``
9
-
-
-
1+8
-
-
-
-
3+6
-
1+8
9
8
R
O
T
A
T
O
R
S
-
-
9
-
-
8
-
9
-
9
-
-
9
6
2
1
2
6
9
1
-
-
-
-
-
-
-
-
-
-
9
8
R
O
T
A
T
O
R
S
-
-
9
-
-
8
-
9
-
9

 

 

8
R
O
T
A
T
O
R
S
-
-
-
-
-
--
-
-
-
-
-
-
6
-
-
-
6
-
1
+
=
13
1+3
=
4
=
4
=
4
-
-
15
-
-
-
15
-
19
+
=
49
4+9
=
13
1+3
4
=
4
8
R
O
T
A
T
O
R
S
-
-
-
-
-
--
-
-
-
-
-
9
-
2
1
2
-
9
-
+
=
23
2+6
=
8
=
5
=
5
-
18
-
20
1
20
-
18
-
+
=
77
7+7
=
14
1+4
5
=
5
8
R
O
T
A
T
O
R
S
-
-
-
-
-
--
-
-
-
-
-
18
15
20
1
20
15
18
19
+
=
126
1+2=6
=
9
=
9
=
9
-
9
6
2
1
2
6
9
1
+
=
36
3+6
=
9
=
9
=
9
8
R
O
T
A
T
O
R
S
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
1
-
-
1
occurs
x
2
=
2
=
2
``-
-
-
2
-
2
-
-
-
-
-
2
occurs
x
2
=
4
=
4
-
-
6
-
-
-
6
-
-
-
-
6
occurs
x
2
=
12
1+2
3
-
9
-
-
-
-
-
9
-
-
-
9
occurs
x
2
=
18
1+8
9
8
R
O
T
A
T
O
R
S
-
-
18
-
-
8
-
36
-
18
-
9
-``
-
-
-
-``
9
-
-
-
1+8
-
-
-
-
3+6
-
1+8
8
R
O
T
A
T
O
R
S
-
-
9
-
-
8
-
9
-
9
-
9
6
2
1
2
6
9
1
-
-
-
-
-
-
-
-
-
-
8
R
O
T
A
T
O
R
S
-
-
9
-
-
8
-
9
-
9

 

 

-
ROTATOR
-
-
-
1
R
18
9
9
3
O+T+A
36
9
9
3
T+O+R
52
17
8
7
ROTATOR
53
35
26
-
-
5+3
3+5
2+6
7
ROTATOR
8
8
8

 

 

-
7
R
O
T
A
T
O
R
-
-
-
-
-
--
-
-
-
-
-
-
-
6
-
-
-
6
-
+
=
12
1+3
=
3
=
3
=
3
-
-
-
15
-
-
-
15
-
+
=
30
3+0
=
3
=
3
=
3
-
7
R
O
T
A
T
O
R
-
-
-
-
-
--
-
-
-
-
-
-
9
-
2
1
2
-
9
+
=
23
2+6
=
8
=
5
=
5
-
-
18
-
20
1
20
-
18
+
=
77
7+7
=
14
1+4
5
=
5
-
7
R
O
T
A
T
O
R
-
-
-
-
-
--
-
-
-
-
-
-
18
15
20
1
20
15
18
+
=
107
1+0=7
=
8
=
8
=
8
-
-
9
6
2
1
2
6
9
+
=
35
3+5
=
8
=
8
=
8
-
7
R
O
T
A
T
O
R
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
1
occurs
x
1
=
1
=
1
-
``-
-
-
2
-
2
-
-
-
-
2
occurs
x
2
=
4
=
4
3
-
-
-
-
-
-
-
-
-
-
3
THREE
3
-
-
-
-
-
4
-
-
-
-
-
-
-
-
-
-
4
FOUR
4
-
-
-
-
-
5
-
-
-
-
-
-
-
-
-
-
5
FIVE
5
-
-
-
-
-
-
-
-
6
-
-
-
6
-
-
-
6
occurs
x
2
=
12
1+2
3
7
-
-
-
-
-
-
-
-
-
-
7
SEVEN
7
-
-
-
-
-
8
-
-
-
-
-
-
-
-
-
-
8
EIGHT
8
-
-
-
-
-
-
-
9
-
-
-
-
-
9
-
-
9
occurs
x
2
=
18
1+8
9
27
7
R
O
T
A
T
O
R
-
-
18
-
-
8
-
35
-
17
2+7
-
9
-``
-
-
-
-``
9
-
-
1+8
-
-
-
-
3+5
-
1+7
9
7
R
O
T
A
T
O
R
-
-
9
-
-
8
-
8
-
8
-
-
9
6
2
1
2
6
9
-
-
-
-
-
-
-
-
-
-
9
7
R
O
T
A
T
O
R
-
-
9
-
-
8
-
8
-
8

 

 

-
7
R
O
T
A
T
O
R
-
-
-
-
-
--
-
-
-
-
-
-
-
6
-
-
-
6
-
+
=
12
1+3
=
3
=
3
=
3
-
-
-
15
-
-
-
15
-
+
=
30
3+0
=
3
=
3
=
3
-
7
R
O
T
A
T
O
R
-
-
-
-
-
--
-
-
-
-
-
-
9
-
2
1
2
-
9
+
=
23
2+6
=
8
=
5
=
5
-
-
18
-
20
1
20
-
18
+
=
77
7+7
=
14
1+4
5
=
5
-
7
R
O
T
A
T
O
R
-
-
-
-
-
--
-
-
-
-
-
-
18
15
20
1
20
15
18
+
=
107
1+0=7
=
8
=
8
=
8
-
-
9
6
2
1
2
6
9
+
=
35
3+5
=
8
=
8
=
8
-
7
R
O
T
A
T
O
R
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
1
occurs
x
1
=
1
=
1
-
``-
-
-
2
-
2
-
-
-
-
2
occurs
x
2
=
4
=
4
3
-
-
-
-
-
-
-
-
-
-
3
-
3
-
-
-
-
-
4
-
-
-
-
-
-
-
-
-
-
4
-
4
-
-
-
-
-
5
-
-
-
-
-
-
-
-
-
-
5
-
5
-
-
-
-
-
-
-
-
6
-
-
-
6
-
-
-
6
occurs
x
2
=
12
1+2
3
7
-
-
-
-
-
-
-
-
-
-
7
-
7
-
-
-
-
-
8
-
-
-
-
-
-
-
-
-
-
8
-
8
-
-
-
-
-
-
-
9
-
-
-
-
-
9
-
-
9
occurs
x
2
=
18
1+8
9
27
7
R
O
T
A
T
O
R
-
-
18
-
-
8
-
35
-
17
2+7
-
9
-``
-
-
-
-``
9
-
-
1+8
-
-
-
-
3+5
-
1+7
9
7
R
O
T
A
T
O
R
-
-
9
-
-
8
-
8
-
8
-
-
9
6
2
1
2
6
9
-
-
-
-
-
-
-
-
-
-
9
7
R
O
T
A
T
O
R
-
-
9
-
-
8
-
8
-
8

 

 

7
R
O
T
A
T
O
R
-
-
-
-
-
--
-
-
-
-
-
-
6
-
-
-
6
-
+
=
12
1+3
=
3
=
3
=
3
-
-
15
-
-
-
15
-
+
=
30
3+0
=
3
=
3
=
3
7
R
O
T
A
T
O
R
-
-
-
-
-
--
-
-
-
-
-
9
-
2
1
2
-
9
+
=
23
2+6
=
8
=
5
=
5
-
18
-
20
1
20
-
18
+
=
77
7+7
=
14
1+4
5
=
5
7
R
O
T
A
T
O
R
-
-
-
-
-
--
-
-
-
-
-
18
15
20
1
20
15
18
+
=
107
1+0=7
=
8
=
8
=
8
-
9
6
2
1
2
6
9
+
=
35
3+5
=
8
=
8
=
8
7
R
O
T
A
T
O
R
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
1
occurs
x
1
=
1
=
1
``-
-
-
2
-
2
-
-
-
-
2
occurs
x
2
=
4
=
4
-
-
6
-
-
-
6
-
-
-
6
occurs
x
2
=
12
1+2
3
-
9
-
-
-
-
-
9
-
-
9
occurs
x
2
=
18
1+8
9
7
R
O
T
A
T
O
R
-
-
18
-
-
8
-
35
-
17
-
9
-``
-
-
-
-``
9
-
-
1+8
-
-
-
-
3+5
-
1+7
7
R
O
T
A
T
O
R
-
-
9
-
-
8
-
8
-
8
-
9
6
2
1
2
6
9
-
-
-
-
-
-
-
-
-
-
7
R
O
T
A
T
O
R
-
-
9
-
-
8
-
8
-
8

 

 

 

The Upside Down of the Downside Up

 

 

A
T
U
M
-
R
A
-
A
R
-
M
U
T
A
1
20
21
13
-
18
1
-
1
18
-
13
21
20
1
1
2
3
4
-
9
1
-
1
9
-
4
3
2
1
A
T
U
M
-
R
A
-
A
R
-
M
U
T
A
1
-
-
-
-
-
1
-
1
-
-
-
-
-
1
-
2
-
-
-
-
-
-
-
-
-
-
-
2
-
-
-
3
-
-
-
-
-
-
-
-
-
3
-
-
-
-
-
4
-
-
-
-
-
-
-
4
-
-
-
-
-
-
-
-
9
-
-
-
9
-
-
-
-
-
A
T
U
M
-
R
A
-
A
R
-
M
U
T
A

 

 

-
-
-
-
9
-
-
-
9
-
-
-
-
-
-
-
4
-
-
-
-
-
4
-
-
-
-
-
3
-
-
-
-
-
-
-
3
-
-
-
2
-
-
-
-
-
-
-
-
-
2
-
1
-
-
-
-
1
-
1
-
-
-
-
1
A
T
U
M
R
A
-
A
R
M
U
T
A
1
20
21
13
18
1
-
1
18
13
21
20
1
1
2
3
4
9
1
-
1
9
4
3
2
1
A
T
U
M
R
A
-
A
R
M
U
T
A
1
2
3
4
9
1
-
1
9
4
3
2
1
A
T
U
M
R
A
-
A
R
M
U
T
A

 

 

-
-
-
4
-
4
-
-
-
-
-
3
-
-
-
3
-
-
-
2
-
-
-
-
-
2
-
1
-
-
-
-
-
-
-
1
A
T
U
M
-
M
U
T
A
1
20
21
13
-
13
21
20
1
1
2
3
4
-
4
3
2
1
A
T
U
M
-
M
U
T
A
1
2
3
4
-
4
3
2
1
A
T
U
M
-
M
U
T
A

 

 

-
-
-
4
4
-
-
-
-
-
3
-
-
3
-
-
-
2
-
-
-
-
2
-
1
-
-
-
-
-
-
1
A
T
U
M
M
U
T
A
1
20
21
13
13
21
20
1
1
2
3
4
4
3
2
1
A
T
U
M
M
U
T
A
1
2
3
4
4
3
2
1
A
T
U
M
M
U
T
A

 

 

6
A
T
U
M
-
R
A
-
-
-
-
-
--
-
-
`-
1
20
21
13
-
18
1
+
=
74
7+4
=
11
1+1
2
-
1
2
3
4
-
9
1
+
=
20
2+0
=
2
-
2
6
A
T
U
M
-
R
A
-T
-
-
-
-
-
-
-
-
1
-
-
-
-
-
1
-
-
1
occurs
x
2
=
2
-
-
2
-
-
-
-
-
-
-
2
occurs
x
1
=
2
-
-
-
3
-
-
-
-
-
-
3
occurs
x
1
=
3
-
-
-
-
4
-
-
-
-
-
4
occurs
x
1
=
4
-
-
-
-
-
-
9
-
-
-
9
occurs
x
1
=
9
6
A
T
U
M
-
R
A
-
-
19
-
-
6
-
20
-
-
-
-
-
-
9
-
-
-
1+9
-
-
-
Q
2+0
6
A
T
U
M
-
R
A
-
-
10
-
-
6
-
2
-
-
-
-
-
-
9
-
-
-
1+0
-
-
-
-
Q
6
A
T
U
M
-
R
A
-
-
1
-
-
6
-
2

 

 

10
LOVE + EVOLVE
-
-
-
-
LOVE
-
-
-
-
L+O
27
9
9
-
V+E
27
9
9
-
EVOLVE
-
-
-
-
E+V
27
9
9
-
O+L
27
9
9
-
V+E
27
9
9
-
LOVE EVOLVE
-
-
-
-
-
-
-
-
-
-
-
-
-
10
LOVE + EVOLVE
135
45
9

 

 

IN SEARCH OF SCHRODINGER'S CAT

 John Gribbin 1984

"QUANTUM PHYSICS AND REALITY"

 

7
QUANTUM
107
26
8
7
PHYSICS
99
36
9
3
AND
19
10
1
7
REALITY
90
36
9
24
Add to Reduce
315
108
27
2+4
Reduce to Deduce
3+1+5
1+0+8
2+7
6
Essence of Number
9
9
9

 

 

7
SERVICE
-
-
-
-
S+E
24
15
6
R
R
18
9
9
-
V
22
4
4
-
I
9
9
9
-
C+E
8
8
8
7
SERVICE
81
45
36
-
-
8+1
4+5
3+6
7
SERVICE
9
9
9

 

 

A TO Z
351
126
9

 

 

9
ALPHA BETA
66
30
3
8
ALPHABET
65
29
2
9
TWENTY SIX
159
42
6
7
LETTERS
99
27
9

 

 

15
ANUBIS A NUMBER IS
-
-
-
1
ANUBIS
66
30
3
-
A
1
1
1
1
NUMBER
73
28
1
2
IS
28
19
1
15
ANUBIS A NUMBER IS
168
78
6
1+5
1+6+8
7+8
-
6
ANUBIS A NUMBER IS
15
15
6
-
1+5
1+5
-
6
ANUBIS A NUMBER IS
6
6
6

 

 

18
THE MAGICAL ALPHABET
-
-
-
1
THE
33
15
6
-
MAGICAL
46
28
1
1
ALPHABET
65
29
2
18
THE MAGICAL ALPHABET
144
72
9
1+8
1+4+4
7+2
-
9
THE MAGICAL ALPHABET
9
9
9

 

 

-
18
T
H
E
-
M
A
G
I
C
A
L
-
A
L
P
H
A
B
E
T
-
-
-
-
-
--
-
-
-
-
-
-
-
8
-
-
-
-
-
9
-
-
-
-
-
-
-
8
-
-
-
-
+
=
25
2+5
=
7
=
7
=
7
-
18
T
H
E
-
M
A
G
I
C
A
L
-
A
L
P
H
A
B
E
T
-
-
-
-
-
--
-
-
-
-
-
-
2
-
5
-
4
1
7
-
3
1
3
-
1
3
7
-
1
2
5
2
+
=
47
4+7
=
11
1+1
2
=
2
-
-
20
-
5
-
13
1
7
-
3
1
12
-
1
12
16
-
1
2
5
20
+
=
119
1+1+9
=
11
1+1
2
=
2
-
18
T
H
E
-
M
A
G
I
C
A
L
-
A
L
P
H
A
B
E
T
-
-
-
-
-
--
-
-
-
-
-
-
20
8
5
-
13
1
7
9
3
1
12
-
1
12
16
8
1
2
5
20
+
=
144
1+4+4
=
9
=
9
=
9
-
-
2
8
5
-
4
1
7
9
3
1
3
-
1
3
7
8
1
2
5
2
+
=
72
7+2
=
9
=
9
=
9
-
18
T
H
E
-
M
A
G
I
C
A
L
-
A
L
P
H
A
B
E
T
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
1
-
-
1
-
-
-
1
-
-
-
-
-
1
occurs
x
4
=
4
=
4
-
-
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
2
-
2
-
-
2
occurs
x
3
=
6
=
6
-
-
-
-
-
-
--
-
-
-
3
-
3
-
-
3
-
-
-
-
-
-
-
-
3
occurs
x
3
=
9
=
9
-
-
-
-
-
-
4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
4
occurs
x
1
=
4
=
4
-
-
-
-
5
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
5
-
-
-
5
occurs
x
2
=
10
1+0
1
6
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
6
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
7
occurs
x
2
=
14
1+4
5
-
-
-
8
-
-
-
-
-
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
8
occurs
x
2
=
16
1+6
7
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
occurs
x
1
=
9
=
9
6
18
T
H
E
-
M
A
G
I
C
A
L
-
A
L
P
H
A
B
E
T
-
-
39
-
-
18
-
72
-
45
-
1+8
-
-
-
-
--
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
12
-
-
1+8
-
7+2
-
4+5
6
9
T
H
E
-
M
A
G
I
C
A
L
-
A
L
P
H
A
B
E
T
-
-
3
-
-
9
-
9
-
9

 

 

THE USBORNE BOOK OF

FACTS AND LISTS

Lynn Bressler (no date)

Page 82

10 most spoken languages
Chinese 700,000,000 English 400,000,000 Russian 265,000,000 Spanish 240,000,000 Hindustani 230,000,000 Arabic 146,000,000 Portuguese 145,000,000 Bengali 144,000,000 German 119,000,000 Japanese 116,000,000

The first alphabet
The Phoenicians, who once lived where Syria, Jordan and Lebanon are today, had an alphabet of 29 letters as early as 1,700 BC. It was adopted by the Greeks and the Romans. Through the Romans, who went on to conquer most of Europe, it became the alphabet of Western countries.

Sounds strange
One tribe of Mexican Indians hold entire conversations just by whistling. The different pitches provide meaning.

The Rosetta Stone
 The Rosetta Stone was found by Napoleon in the sands of Egypt. It dates to about 196 BC.
On it is an inscription in hieroglyphics and a translation in Greek. , Because scholars knew ancient Greek, they could work out what the Egyptian hieroglyphics meant. From this they learned the language of the ancient Egyptians.

Did You KnowMany Chinese cannot understand each other. They have different ways of speaking (called dialects) in different
parts of the country. But today in schools allover China, the children are being taught one dialect (Mandarin), so that one day all Chinese will understand each other.

Translating computers
Computers can be used to help people of different nationalities, who do not know each others' language, talk to each other. By giving a computer a message in one language it will translate it into another specified language.

Worldwide language
English is spoken either as a first or second language in at least 45 countries. This is more than any other language. It is the language of international business and scientific conferences and is used by airtraffic controllers worldwide. In all, about one third of the world speaks it.

Page 83

Earliest writing Chinese writing has been found on pottery, and even on a tortoise shell, going back 6,000 years. Pictures made the basis for their writing, each picture showing an object or idea. Probably the earliest form of writing came from the Middle East, where Iraq and Iran are now. This region was then ruled by the Sumerians.

The most words

English has more words in it than any other language. There are about1 million in all, a third of which are technical terms. Most
people only use about 1 per cent of the words available, that is, about 10,000. William Shakespeare is reputed to have made most use of the English vocabulary.

A scientific word describing a process in the human cell is 207,000 letters long. This makes this single word equal in length to a short novel or about 80 typed sheets of A4 paper.

Many tongues
A Frenchman, named Georges Henri Schmidt, is fluent (meaning he reads and writes well) in 31 different languages.

International language
Esperanto was invented in the 1880s by a Pole, Dr Zamenhof. It was hoped that it would become the international language of Europe. It took words from many European countries and has a very easy grammar that can be learned in an hour or two.
The same language

The languages of India and Europe may originally come from just one source. Many words in different languages sound similar. For example, the word for King in Latin is Rex, in Indian, Raj, in Italian Re, in French Roi and in Spanish Rey. The original language has been named Indo-European. Basque, spoken in the French and Spanish Pyrenees, is an exception. It seems to have a different source which is still unknown.

Number of alphabets
There are 65 alphabets in use in the world today. Here are some of them: Roman
ABCDEFGHUKLMNOPQRS Greek  Russian (Cyrillic) Hebrew  Chinese (examples omitted)

 

 

THE

MAGICALALPHABET

ABCDEFGHIJKLMNOPQRSTUVWXYZZYXWVUTSRQPONMLKJIHGFEDCBA

12345678910111213141516171819202122232425262625242322212019181716151413121110987654321

 

26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
8
9
-
-
-
-
5
6
-
-
-
1
-
-
-
-
6
-
8
+
=
43
4+3
=
7
-
7
-
7
-
-
-
-
-
-
-
-
8
9
-
-
-
-
14
15
-
-
-
19
-
-
-
-
24
-
26
+
=
115
1+1+5
=
7
-
7
-
7
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
-
-
1
2
3
4
-
-
7
8
9
-
2
3
4
5
-
7
-
+
=
83
8+3
=
11
1+1
2
-
2
-
1
2
3
4
5
6
7
-
-
10
11
12
13
-
-
16
17
18
-
20
21
22
23
-
25
-
+
=
236
2+3+6
=
11
1+1
2
-
2
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
+
=
351
3+5+1
=
9
-
9
-
9
-
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
+
=
126
1+2+6
=
9
-
9
-
9
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
+
=
1
occurs
x
3
=
3
-
3
-
-
2
-
-
-
-
-
-
-
-
2
-
-
-
-
-
-
-
-
2
-
-
-
-
-
-
+
=
2
occurs
x
3
=
6
-
6
-
-
-
3
-
-
-
-
-
-
-
-
3
-
-
-
-
-
-
-
-
3
-
-
-
-
-
+
=
3
occurs
x
3
=
9
-
9
-
-
-
-
4
-
-
-
-
-
-
-
-
4
-
-
-
-
-
-
-
-
4
-
-
-
-
+
=
4
occurs
x
3
=
12
1+2
3
-
-
-
-
-
5
-
-
-
-
-
-
-
-
5
-
-
-
-
-
-
-
-
5
-
-
-
+
=
5
occurs
x
3
=
15
1+5
6
-
-
-
-
-
-
6
-
-
-
-
-
-
-
-
6
-
-
-
-
-
-
-
-
6
-
-
+
=
6
occurs
x
3
=
18
1+8
9
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
-
7
-
+
=
7
occurs
x
3
=
21
2+1
3
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
8
+
=
8
occurs
x
3
=
24
2+4
6
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
+
=
9
occurs
x
2
=
18
1+8
9
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
45
-
-
26
-
126
-
54
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
4+5
-
-
2+6
-
1+2+6
-
5+4
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
9
-
-
8
-
9
-
9
-
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
-
-
-
-
-
-
-
-
-
-
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
9
-
-
8
-
9
-
9

 

 

BEYOND THE VEIL ANOTHER VEIL ANOTHER VEIL BEYOND

 

 

18
THE ENGLISH ALPHABET
-
-
-
1
THE
33
15
6
-
ENGLISH
74
38
2
1
ALPHABET
65
29
2
18
THE ENGLISH ALPHABET
172
82
10
1+8
1+7+2
8+2
1+0
9
THE ENGLISH ALPHABET
10
10
10
-
1+0
1+0
1+0
9
THE ENGLISH ALPHABET
1
1
1

 

 

-
18
T
H
E
-
E
N
G
L
I
S
H
-
A
L
P
H
A
B
E
T
-
-
-
-
-
--
-
-
-
-
-
-
-
8
-
-
-
5
-
-
9
1
8
-
-
-
-
8
-
-
-
-
+
=
39
3+9
=
12
1+2
3
=
3
-
-
-
8
-
-
-
14
-
-
9
19
8
-
-
-
-
8
-
-
-
-
+
=
66
6+6
=
12
1+2
3
=
3
-
18
T
H
E
-
E
N
G
L
I
S
H
-
A
L
P
H
A
B
E
T
-
-
-
-
-
--
-
-
-
-
-
-
2
-
5
-
5
-
7
3
-
-
-
-
1
3
7
-
1
2
5
2
+
=
43
4+3
=
7
=
7
=
7
-
-
20
-
5
-
5
-
7
12
-
-
-
-
1
12
16
-
1
2
5
20
+
=
106
1+0+6
=
7
=
7
=
7
-
18
T
H
E
-
E
N
G
L
I
S
H
-
A
L
P
H
A
B
E
T
-
-
-
-
-
--
-
-
-
-
-
-
20
8
5
-
5
14
7
12
9
19
8
-
1
12
16
8
1
2
5
20
+
=
172
1+7+2
=
10
1+0
1
=
1
-
-
2
8
5
-
5
5
7
3
9
1
8
-
1
3
7
8
1
2
5
2
+
=
82
8+2
=
10
1+0
1
=
1
-
18
T
H
E
-
E
N
G
L
I
S
H
-
A
L
P
H
A
B
E
T
-
-
-
-
-
--
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
1
-
-
-
1
-
-
-
-
-
1
occurs
x
3
=
3
=
3
-
-
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
2
-
2
-
-
2
occurs
x
3
=
6
=
6
-
-
-
-
-
-
--
-
-
3
-
-
-
-
-
3
-
-
-
-
-
-
-
-
3
occurs
x
2
=
6
=
6
4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
4
FOUR
4
-
-
-
-
-
-
-
-
-
5
-
5
5
-
-
-
-
-
-
-
-
-
-
-
-
5
-
-
-
5
occurs
x
4
=
20
2+0
2
6
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
6
SIX
6
-
-
-
-
-
-
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
7
occurs
x
2
=
14
1+4
5
-
-
-
8
-
-
-
-
-
-
-
-
8
-
-
-
-
8
-
-
-
-
-
-
8
occurs
x
3
=
24
2+4
6
-
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
9
occurs
x
1
=
9
=
9
10
18
T
H
E
-
E
N
G
L
I
S
H
-
A
L
P
H
A
B
E
T
-
-
35
-
-
18
-
82
-
37
1+0
1+8
-
-
-
-
--
-
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
3+5
-
-
1+8
-
8+2
-
3+7
1
9
T
H
E
-
E
N
G
L
I
S
H
-
A
L
P
H
A
B
E
T
-
-
8
-
-
9
-
10
-
10
-
-
2
8
5
-
5
5
7
3
9
1
8
-
1
3
7
8
1
2
5
2
-
-
-
-
-
-
-
1+0
-
1+0
1
9
T
H
E
-
E
N
G
L
I
S
H
-
A
L
P
H
A
B
E
T
-
-
8
-
-
9
-
1
-
1

 

 

3
THE
33
15
6
7
ENGLISH
74
38
2
8
ALPHABET
65
29
2

 

 

T
=
2
-
3
THE
33
15
6
E
=
5
-
7
ENGLISH
74
47
2
A
=
1
-
8
ALPHABET
65
29
2
-
-
8
4
18
First Total
172
91
10
-
-
1+0
-
1+8
Add to Reduce
1+7+2
9+1
1+0
-
-
1
-
9
Second Total
10
10
1
-
-
-
-
-
Reduce to Deduce
1+0
1+0
-
-
-
1
-
9
Essence of Number
1
1
5

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
T
=
2
-
3
THE
33
15
6
-
-
-
-
-
-
-
-
-
-
E
=
5
-
7
ENGLISH
74
47
2
-
-
-
-
-
-
-
-
-
-
A
=
1
-
8
ALPHABET
65
29
2
-
-
-
-
-
-
-
-
-
-
-
-
8
4
18
First Total
172
91
10
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
T
=
2
1
1
T
20
2
2
-
-
2
-
4
-
6
-
-
-
H
=
8
2
1
H
8
8
8
-
-
-
-
4
-
6
-
8
-
E
=
5
3
1
E
5
5
5
-
-
-
-
4
5
6
-
-
-
-
-
15
-
3
-
33
15
15
-
-
-
-
12
-
18
-
-
-
E
=
5
4
1
E
5
5
5
-
-
-
-
4
5
6
-
-
-
N
=
5
5
1
N
14
5
5
-
-
-
-
4
5
6
-
-
-
G
=
7
6
1
G
7
7
7
-
-
-
-
4
-
6
7
-
-
L
=
3
7
1
L
12
3
3
-
-
-
3
4
-
6
-
-
-
I
=
9
8
1
I
9
9
9
-
-
-
-
4
-
6
-
-
9
S
=
1
9
1
S
19
10
1
-
1
-
-
4
-
6
-
-
-
H
=
8
10
1
H
8
8
8
-
-
-
-
4
-
6
-
8
-
-
-
38
-
7
-
74
47
38
-
-
-
-
28
-
42
-
-
-
A
=
1
11
1
A
1
1
1
-
1
-
-
4
-
6
-
-
-
L
=
3
12
1
L
12
3
3
-
-
-
3
4
-
6
-
-
-
P
=
7
13
1
P
16
7
7
-
-
-
-
4
-
6
7
-
-
H
=
8
14
1
H
8
8
8
-
-
-
-
4
-
6
-
8
-
A
=
1
15
1
A
1
1
1
-
1
-
-
4
-
6
-
-
-
B
=
2
16
1
B
2
2
2
-
-
2
-
4
-
6
-
-
-
E
=
5
17
1
E
5
5
5
-
-
-
-
4
5
6
-
-
-
T
=
2
18
1
T
20
2
2
-
-
2
-
4
-
6
-
-
-
29
-
8
-
65
29
29
-
-
-
-
32
-
48
-
-
-
-
-
-
-
-
-
-
-
-
-
3
6
6
4
20
6
14
24
9
T
=
2
-
3
THE
33
15
6
-
-
-
-
-
2+0
-
1+4
2+4
-
E
=
5
-
7
ENGLISH
74
47
2
-
3
6
6
4
2
6
5
6
9
A
=
1
-
8
ALPHABET
65
29
2
-
-
-
-
-
-
-
-
-
-
-
-
8
4
18
First Total
172
91
10
-
3
6
6
4
2
6
5
6
9
-
-
1+0
-
1+8
Add to Reduce
1+7+2
9+1
1+0
-
-
-
-
-
-
-
-
-
-
-
-
1
-
9
Second Total
10
10
1
-
3
6
6
4
2
6
5
6
9
-
-
-
-
-
Reduce to Deduce
1+0
1+0
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
9
Essence of Number
1
1
5
-
3
6
6
4
2
6
5
6
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
T
=
2
-
3
THE
33
15
6
-
-
-
-
-
-
-
-
-
-
E
=
5
-
7
ENGLISH
74
47
2
-
-
-
-
-
-
-
-
-
-
A
=
1
-
8
ALPHABET
65
29
2
-
-
-
-
-
-
-
-
-
-
-
-
8
4
18
First Total
172
91
10
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
T
=
2
1
1
T
20
2
2
-
-
2
-
4
-
6
-
-
-
H
=
8
2
1
H
8
8
8
-
-
-
-
4
-
6
-
8
-
E
=
5
3
1
E
5
5
5
-
-
-
-
4
5
6
-
-
-
E
=
5
4
1
E
5
5
5
-
-
-
-
4
5
6
-
-
-
N
=
5
5
1
N
14
5
5
-
-
-
-
4
5
6
-
-
-
G
=
7
6
1
G
7
7
7
-
-
-
-
4
-
6
7
-
-
L
=
3
7
1
L
12
3
3
-
-
-
3
4
-
6
-
-
-
I
=
9
8
1
I
9
9
9
-
-
-
-
4
-
6
-
-
9
S
=
1
9
1
S
19
10
1
-
1
-
-
4
-
6
-
-
-
H
=
8
10
1
H
8
8
8
-
-
-
-
4
-
6
-
8
-
A
=
1
11
1
A
1
1
1
-
1
-
-
4
-
6
-
-
-
L
=
3
12
1
L
12
3
3
-
-
-
3
4
-
6
-
-
-
P
=
7
13
1
P
16
7
7
-
-
-
-
4
-
6
7
-
-
H
=
8
14
1
H
8
8
8
-
-
-
-
4
-
6
-
8
-
A
=
1
15
1
A
1
1
1
-
1
-
-
4
-
6
-
-
-
B
=
2
16
1
B
2
2
2
-
-
2
-
4
-
6
-
-
-
E
=
5
17
1
E
5
5
5
-
-
-
-
4
5
6
-
-
-
T
=
2
18
1
T
20
2
2
-
-
2
-
4
-
6
-
-
-
-
-
-
-
-
-
-
-
-
-
3
6
6
4
20
6
14
24
9
T
=
2
-
3
THE
33
15
6
-
-
-
-
-
2+0
-
1+4
2+4
-
E
=
5
-
7
ENGLISH
74
47
2
-
3
6
6
4
2
6
5
6
9
A
=
1
-
8
ALPHABET
65
29
2
-
-
-
-
-
-
-
-
-
-
-
-
8
4
18
First Total
172
91
10
-
3
6
6
4
2
6
5
6
9
-
-
1+0
-
1+8
Add to Reduce
1+7+2
9+1
1+0
-
-
-
-
-
-
-
-
-
-
-
-
1
-
9
Second Total
10
10
1
-
3
6
6
4
2
6
5
6
9
-
-
-
-
-
Reduce to Deduce
1+0
1+0
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
9
Essence of Number
1
1
5
-
3
6
6
4
2
6
5
6
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
T
=
2
-
3
THE
33
15
6
-
-
-
-
-
-
-
-
-
-
E
=
5
-
7
ENGLISH
74
47
2
-
-
-
-
-
-
-
-
-
-
A
=
1
-
8
ALPHABET
65
29
2
-
-
-
-
-
-
-
-
-
-
-
-
8
4
18
First Total
172
91
10
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
S
=
1
9
1
S
19
10
1
-
1
-
-
4
-
6
-
-
-
A
=
1
11
1
A
1
1
1
-
1
-
-
4
-
6
-
-
-
A
=
1
15
1
A
1
1
1
-
1
-
-
4
-
6
-
-
-
T
=
2
1
1
T
20
2
2
-
-
2
-
4
-
6
-
-
-
B
=
2
16
1
B
2
2
2
-
-
2
-
4
-
6
-
-
-
T
=
2
18
1
T
20
2
2
-
-
2
-
4
-
6
-
-
-
L
=
3
7
1
L
12
3
3
-
-
-
3
4
-
6
-
-
-
L
=
3
12
1
L
12
3
3
-
-
-
3
4
-
6
-
-
-
E
=
5
3
1
E
5
5
5
-
-
-
-
4
5
6
-
-
-
E
=
5
4
1
E
5
5
5
-
-
-
-
4
5
6
-
-
-
N
=
5
5
1
N
14
5
5
-
-
-
-
4
5
6
-
-
-
E
=
5
17
1
E
5
5
5
-
-
-
-
4
5
6
-
-
-
G
=
7
6
1
G
7
7
7
-
-
-
-
4
-
6
7
-
-
P
=
7
13
1
P
16
7
7
-
-
-
-
4
-
6
7
-
-
H
=
8
2
1
H
8
8
8
-
-
-
-
4
-
6
-
8
-
H
=
8
10
1
H
8
8
8
-
-
-
-
4
-
6
-
8
-
H
=
8
14
1
H
8
8
8
-
-
-
-
4
-
6
-
8
-
I
=
9
8
1
I
9
9
9
-
-
-
-
4
-
6
-
-
9
-
-
-
-
-
-
-
-
-
-
3
6
6
4
20
6
14
24
9
T
=
2
-
3
THE
33
15
6
-
-
-
-
-
2+0
-
1+4
2+4
-
E
=
5
-
7
ENGLISH
74
47
2
-
3
6
6
4
2
6
5
6
9
A
=
1
-
8
ALPHABET
65
29
2
-
-
-
-
-
-
-
-
-
-
-
-
8
4
18
First Total
172
91
10
-
3
6
6
4
2
6
5
6
9
-
-
1+0
-
1+8
Add to Reduce
1+7+2
9+1
1+0
-
-
-
-
-
-
-
-
-
-
-
-
1
-
9
Second Total
10
10
1
-
3
6
6
4
2
6
5
6
9
-
-
-
-
-
Reduce to Deduce
1+0
1+0
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
9
Essence of Number
1
1
5
-
3
6
6
4
2
6
5
6
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
5
7
8
9
T
=
2
-
3
THE
33
15
6
-
-
-
-
-
-
-
-
E
=
5
-
7
ENGLISH
74
47
2
-
-
-
-
-
-
-
-
A
=
1
-
8
ALPHABET
65
29
2
-
-
-
-
-
-
-
-
-
-
8
4
18
First Total
172
91
10
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
2
3
5
7
8
9
S
=
1
9
1
S
19
10
1
-
1
-
-
-
-
-
-
A
=
1
11
1
A
1
1
1
-
1
-
-
-
-
-
-
A
=
1
15
1
A
1
1
1
-
1
-
-
-
-
-
-
T
=
2
1
1
T
20
2
2
-
-
2
-
-
-
-
-
B
=
2
16
1
B
2
2
2
-
-
2
-
-
-
-
-
T
=
2
18
1
T
20
2
2
-
-
2
-
-
-
-
-
L
=
3
7
1
L
12
3
3
-
-
-
3
-
-
-
-
L
=
3
12
1
L
12
3
3
-
-
-
3
-
-
-
-
E
=
5
3
1
E
5
5
5
-
-
-
-
5
-
-
-
E
=
5
4
1
E
5
5
5
-
-
-
-
5
-
-
-
N
=
5
5
1
N
14
5
5
-
-
-
-
5
-
-
-
E
=
5
17
1
E
5
5
5
-
-
-
-
5
-
-
-
G
=
7
6
1
G
7
7
7
-
-
-
-
-
7
-
-
P
=
7
13
1
P
16
7
7
-
-
-
-
-
7
-
-
H
=
8
2
1
H
8
8
8
-
-
-
-
-
-
8
-
H
=
8
10
1
H
8
8
8
-
-
-
-
-
-
8
-
H
=
8
14
1
H
8
8
8
-
-
-
-
-
-
8
-
I
=
9
8
1
I
9
9
9
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
3
6
6
20
14
24
9
T
=
2
-
3
THE
33
15
6
-
-
-
-
2+0
1+4
2+4
-
E
=
5
-
7
ENGLISH
74
47
2
-
3
6
6
2
5
6
9
A
=
1
-
8
ALPHABET
65
29
2
-
-
-
-
-
-
-
-
-
-
8
4
18
First Total
172
91
10
-
3
6
6
2
5
6
9
-
-
1+0
-
1+8
Add to Reduce
1+7+2
9+1
1+0
-
-
-
-
-
-
-
-
-
-
1
-
9
Second Total
10
10
1
-
3
6
6
2
5
6
9
-
-
-
-
-
Reduce to Deduce
1+0
1+0
-
-
-
-
-
-
-
-
-
-
-
1
-
9
Essence of Number
1
1
5
-
3
6
6
2
5
6
9

 

 

 

O
=
6
-
3
OUT
56
11
2
O
=
6
-
2
OF
21
12
3
Z
=
8
-
4
ZERO
64
28
1
C
=
3
-
6
COMETH
64
28
1
O
=
6
-
3
ONE
34
16
7
Q
Q
29
Q
18
Q
239
95
14
-
-
2+9
-
1+8
-
2+3+9
9+5
1+4
-
-
11
-
9
-
14
14
5
-
-
1+1
-
-
-
1+4
1+4
-
-
-
2
-
9
-
5
5
5

 

 

-
18
T
H
E
-
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
-
8
-
-
-
5
-
-
9
1
8
-
-
-
5
-
-
-
-
-
+
=
36
3+6
=
9
=
9
=
9
-
-
-
8
-
-
-
14
-
-
9
19
8
-
-
-
14
-
-
-
-
-
+
=
72
7+2
=
9
=
9
=
9
-
18
T
H
E
-
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
2
-
5
-
5
-
7
3
-
-
-
-
3
1
-
7
3
1
7
5
+
=
49
4+9
=
13
1+3
4
=
4
-
-
20
-
5
-
5
-
7
12
-
-
-
-
12
1
-
7
21
1
7
5
+
=
103
1+0+3
=
4
=
4
=
4
-
18
T
H
E
-
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
20
8
5
-
5
14
7
12
9
19
8
-
12
1
14
7
21
1
7
5
+
=
175
1+7+5
=
13
1+3
4
=
4
-
-
2
8
5
-
5
5
7
3
9
1
8
-
3
1
5
7
3
1
7
5
+
=
85
8+5
=
13
1+3
4
=
4
-
18
T
H
E
-
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
1
-
-
-
1
-
-
-
-
1
occurs
x
3
=
3
=
3
-
-
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
2
occurs
x
1
=
2
=
2
-
-
-
-
--
-
--
-
-
3
-
-
-
-
3
-
-
-
3
-
-
-
-
-
3
occurs
x
3
=
9
=
9
4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
4
FOUR
4
-
-
-
-
-
-
-
-
-
5
-
5
5
-
-
-
-
-
-
-
-
5
-
-
-
-
5
-
-
5
occurs
x
5
=
25
2+5
7
6
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
6
SIX
6
-
-
-
-
-
-
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
-
7
-
-
7
-
-
-
7
occurs
x
3
=
21
2+1
3
-
-
-
8
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
-
-
-
8
occurs
x
2
=
16
1+6
7
-
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
9
occurs
x
1
=
9
=
9
10
18
T
H
E
-
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
35
-
-
18
-
85
-
40
1+0
1+8
-
-
5
-
5
5
-
-
-
-
-
-
-
-
5
-
-
-
-
5
-
-
3+5
-
-
1+8
-
8+5
-
4+0
1
9
T
H
E
-
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
8
-
-
9
-
13
-
4
-
-
2
8
5
-
5
5
7
3
9
1
8
-
3
1
5
7
3
1
7
5
-
-
-
-
-
-
-
1+3
-
-
1
9
T
H
E
-
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
8
-
-
9
-
4
-
4

 

 

18
T
H
E
-
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
-
-
-
--
-
-
-
-
-
-
8
-
-
-
5
-
-
9
1
8
-
-
-
5
-
-
-
-
-
+
=
36
3+6
=
9
=
9
=
9
-
-
8
-
-
-
14
-
-
9
19
8
-
-
-
14
-
-
-
-
-
+
=
72
7+2
=
9
=
9
=
9
18
T
H
E
-
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
2
-
5
-
5
-
7
3
-
-
-
-
3
1
-
7
3
1
7
5
+
=
49
4+9
=
13
1+3
4
=
4
-
20
-
5
-
5
-
7
12
-
-
-
-
12
1
-
7
21
1
7
5
+
=
103
1+0+3
=
4
=
4
=
4
18
T
H
E
-
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
20
8
5
-
5
14
7
12
9
19
8
-
12
1
14
7
21
1
7
5
+
=
175
1+7+5
=
13
1+3
4
=
4
-
2
8
5
-
5
5
7
3
9
1
8
-
3
1
5
7
3
1
7
5
+
=
85
8+5
=
13
1+3
4
=
4
18
T
H
E
-
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
1
-
-
-
1
-
-
-
-
1
occurs
x
3
=
3
=
3
-
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
2
occurs
x
1
=
2
=
2
-
-
-
--
-
--
-
-
3
-
-
-
-
3
-
-
-
3
-
-
-
-
-
3
occurs
x
3
=
9
=
9
-
-
-
5
-
5
5
-
-
-
-
-
-
-
-
5
-
-
-
-
5
-
-
5
occurs
x
5
=
25
2+5
7
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
-
7
-
-
7
-
-
-
7
occurs
x
3
=
21
2+1
3
-
-
8
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
-
-
-
8
occurs
x
2
=
16
1+6
7
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
9
occurs
x
1
=
9
=
9
18
T
H
E
-
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
35
-
-
18
-
85
-
40
1+8
-
-
5
-
5
5
-
-
-
-
-
-
-
-
5
-
-
-
-
5
-
-
3+5
-
-
1+8
-
8+5
-
4+0
9
T
H
E
-
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
8
-
-
9
-
13
-
4
-
2
8
5
-
5
5
7
3
9
1
8
-
3
1
5
7
3
1
7
5
-
-
-
-
-
-
-
1+3
-
-
9
T
H
E
-
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
8
-
-
9
-
4
-
4

 

 

18
T
H
E
E
N
G
L
I
S
H
L
A
N
G
U
A
G
E
-
-
-
-
-
--
-
-
-
-
-
-
8
-
-
5
-
-
9
1
8
-
-
5
-
-
-
-
-
+
=
36
3+6
=
9
=
9
=
9
-
-
8
-
-
14
-
-
9
19
8
-
-
14
-
-
-
-
-
+
=
72
7+2
=
9
=
9
=
9
18
T
H
E
E
N
G
L
I
S
H
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
2
-
5
5
-
7
3
-
-
-
3
1
-
7
3
1
7
5
+
=
49
4+9
=
13
1+3
4
=
4
-
20
-
5
5
-
7
12
-
-
-
12
1
-
7
21
1
7
5
+
=
103
1+0+3
=
4
=
4
=
4
18
T
H
E
E
N
G
L
I
S
H
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
20
8
5
5
14
7
12
9
19
8
12
1
14
7
21
1
7
5
+
=
175
1+7+5
=
13
1+3
4
=
4
-
2
8
5
5
5
7
3
9
1
8
3
1
5
7
3
1
7
5
+
=
85
8+5
=
13
1+3
4
=
4
18
T
H
E
E
N
G
L
I
S
H
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
1
-
-
-
1
-
-
-
-
1
occurs
x
3
=
3
=
3
-
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
2
occurs
x
1
=
2
=
2
-
-
-
--
--
-
-
3
-
-
-
3
-
-
-
3
-
-
-
-
-
3
occurs
x
3
=
9
=
9
-
-
-
5
5
5
-
-
-
-
-
-
-
5
-
-
-
-
5
-
-
5
occurs
x
5
=
25
2+5
7
-
-
-
-
-
-
7
-
-
-
-
-
-
-
7
-
-
7
-
-
-
7
occurs
x
3
=
21
2+1
3
-
-
8
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
-
-
8
occurs
x
2
=
16
1+6
7
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
9
occurs
x
1
=
9
=
9
18
T
H
E
E
N
G
L
I
S
H
L
A
N
G
U
A
G
E
-
-
35
-
-
18
-
85
-
40
1+8
-
-
5
5
5
-
-
-
-
-
-
-
5
-
-
-
-
5
-
-
3+5
-
-
1+8
-
8+5
-
4+0
9
T
H
E
E
N
G
L
I
S
H
L
A
N
G
U
A
G
E
-
-
8
-
-
9
-
13
-
4
-
2
8
5
5
5
7
3
9
1
8
3
1
5
7
3
1
7
5
-
-
-
-
-
-
-
1+3
-
-
9
T
H
E
E
N
G
L
I
S
H
L
A
N
G
U
A
G
E
-
-
8
-
-
9
-
4
-
4

 

 

E
=
5
-
7
ENGLISH
74
38
2
L
=
3
-
8
LANGUAGE
68
32
5
-
-
10
-
15
First Total
142
79
7
-
-
1+0
-
1+5
Add to Reduce
1+4+2
7+9
-
=-
-
1
-
6
Second Total
7
16
7
-
-
-
-
-
Reduce to Deduce
-
1+6
-
-
-
1
-
6
Essence of Number
7
7
7

 

 

-
15
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
-
-
-
--
-
-
-
-
-
-
-
5
-
-
9
1
8
-
-
-
5
-
-
-
-
-
+
=
28
2+8
=
10
1+0
1
=
1
-
-
-
14
-
-
9
19
8
-
-
-
14
-
-
-
-
-
+
=
64
6+4
=
10
1+0
1
=
1
-
15
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
5
-
7
3
-
-
-
-
3
1
-
7
3
1
7
5
+
=
42
4+2
=
6
=
6
=
6
-
-
5
-
7
12
-
-
-
-
12
1
-
7
21
1
7
5
+
=
78
7+8
=
15
1+5
6
=
6
-
15
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
5
14
7
12
9
19
8
-
12
1
14
7
21
1
7
5
+
=
142
1+4+2
=
7
=
7
=
7
-
-
5
5
7
3
9
1
8
-
3
1
5
7
3
1
7
5
+
=
78
7+0
=
7
=
7
=
7
-
15
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
1
-
-
-
1
-
-
-
-
1
occurs
x
3
=
3
=
3
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
2
TWO
2
-
-
-
-
-
-
-
--
-
-
3
-
-
-
-
3
-
-
-
3
-
-
-
-
-
3
occurs
x
3
=
9
=
9
4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
4
FOUR
4
-
-
-
-
-
-
-
5
5
-
-
-
-
-
-
-
-
5
-
-
-
-
5
-
-
5
occurs
x
4
=
20
2+0
2
6
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
6
SIX
6
-
-
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
-
7
-
-
7
-
-
-
7
occurs
x
3
=
21
2+1
3
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
-
-
-
8
occurs
x
1
=
8
=
8
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
9
occurs
x
1
=
9
=
9
12
15
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
33
-
-
15
-
70
-
34
1+2
1+5
5
5
-
-
-
-
-
-
-
-
5
-
-
-
-
5
-
-
3+3
-
-
1+5
-
7+0
-
3+4
3
6
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
6
-
-
6
-
7
-
7
-
-
5
5
7
3
9
1
8
-
3
1
5
7
3
1
7
5
-
-
-
-
-
-
-
1+3
-
-
3
6
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
6
-
-
6
-
7
-
7

 

 

15
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
-
-
-
--
-
-
-
-
-
-
5
-
-
9
1
8
-
-
-
5
-
-
-
-
-
+
=
28
2+8
=
10
1+0
1
=
1
-
-
14
-
-
9
19
8
-
-
-
14
-
-
-
-
-
+
=
64
6+4
=
10
1+0
1
=
1
15
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
5
-
7
3
-
-
-
-
3
1
-
7
3
1
7
5
+
=
42
4+2
=
6
=
6
=
6
-
5
-
7
12
-
-
-
-
12
1
-
7
21
1
7
5
+
=
78
7+8
=
15
1+5
6
=
6
15
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
5
14
7
12
9
19
8
-
12
1
14
7
21
1
7
5
+
=
142
1+4+2
=
7
=
7
=
7
-
5
5
7
3
9
1
8
-
3
1
5
7
3
1
7
5
+
=
78
7+0
=
7
=
7
=
7
15
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
1
-
-
-
1
-
-
-
-
1
occurs
x
3
=
3
=
3
-
--
-
-
3
-
-
-
-
3
-
-
-
3
-
-
-
-
-
3
occurs
x
3
=
9
=
9
-
5
5
-
-
-
-
-
-
-
-
5
-
-
-
-
5
-
-
5
occurs
x
4
=
20
2+0
2
-
-
-
7
-
-
-
-
-
-
-
-
7
-
-
7
-
-
-
7
occurs
x
3
=
21
2+1
3
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
-
-
-
8
occurs
x
1
=
8
=
8
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
9
occurs
x
1
=
9
=
9
15
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
33
-
-
15
-
70
-
34
1+5
5
5
-
-
-
-
-
-
-
-
5
-
-
-
-
5
-
-
3+3
-
-
1+5
-
7+0
-
3+4
6
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
6
-
-
6
-
7
-
7
-
5
5
7
3
9
1
8
-
3
1
5
7
3
1
7
5
-
-
-
-
-
-
-
1+3
-
-
6
E
N
G
L
I
S
H
-
L
A
N
G
U
A
G
E
-
-
6
-
-
6
-
7
-
7

 

 

15
E
N
G
L
I
S
H
L
A
N
G
U
A
G
E
-
-
-
-
-
--
-
-
-
-
-
-
5
-
-
9
1
8
-
-
5
-
-
-
-
-
+
=
28
2+8
=
10
1+0
1
=
1
-
-
14
-
-
9
19
8
-
-
14
-
-
-
-
-
+
=
64
6+4
=
10
1+0
1
=
1
15
E
N
G
L
I
S
H
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
5
-
7
3
-
-
-
3
1
-
7
3
1
7
5
+
=
42
4+2
=
6
=
6
=
6
-
5
-
7
12
-
-
-
12
1
-
7
21
1
7
5
+
=
78
7+8
=
15
1+5
6
=
6
15
E
N
G
L
I
S
H
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
5
14
7
12
9
19
8
12
1
14
7
21
1
7
5
+
=
142
1+4+2
=
7
=
7
=
7
-
5
5
7
3
9
1
8
3
1
5
7
3
1
7
5
+
=
78
7+0
=
7
=
7
=
7
15
E
N
G
L
I
S
H
L
A
N
G
U
A
G
E
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
1
-
-
-
1
-
-
-
-
1
occurs
x
3
=
3
=
3
-
--
-
-
3
-
-
-
3
-
-
-
3
-
-
-
-
-
3
occurs
x
3
=
9
=
9
-
5
5
-
-
-
-
-
-
-
5
-
-
-
-
5
-
-
5
occurs
x
4
=
20
2+0
2
-
-
-
7
-
-
-
-
-
-
-
7
-
-
7
-
-
-
7
occurs
x
3
=
21
2+1
3
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
-
-
8
occurs
x
1
=
8
=
8
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
9
occurs
x
1
=
9
=
9
15
E
N
G
L
I
S
H
L
A
N
G
U
A
G
E
-
-
33
-
-
15
-
70
-
34
1+5
5
5
-
-
-
-
-
-
-
5
-
-
-
-
5
-
-
3+3
-
-
1+5
-
7+0
-
3+4
6
E
N
G
L
I
S
H
L
A
N
G
U
A
G
E
-
-
6
-
-
6
-
7
-
7
-
5
5
7
3
9
1
8
3
1
5
7
3
1
7
5
-
-
-
-
-
-
-
1+3
-
-
6
E
N
G
L
I
S
H
L
A
N
G
U
A
G
E
-
-
6
-
-
6
-
7
-
7

 

 

7
ENGLISH
74
38
2
8
LANGUAGE
68
32
5
15
First Total
142
79
7
1+5
Add to Reduce
1+4+2
7+9
-
6
Second Total
7
16
7
-
Reduce to Deduce
-
1+6
-
6
Essence of Number
7
7
7

 

 

-
ENGLISH
-
-
-
4
E+N+G+L
38
20
2
1
I
36
18
9
4
S+H
27
9
9
7
ENGLISH
74
38
11
-
-
7+4
3+9
1+1
7
ENGLISH
11
11
2
-
-
1+1
1+1
-
7
ENGLISH
2
2
2

 

 

THE LIGHT IS RISING RISING IS THE LIGHT

 

 

3
THE
33
15
6
7
ENGLISH
74
38
2
8
LANGUAGE
68
32
5

 

 

No curved lines - A.E.F.H.I.K.L.M.N.T.V.W.X.Y.Z.

No straight lines-C.O.S.

No enclosed areas-C.E.F.G.H.I.J.K.L.M.N.S.T.U.V.W.X.Y.Z.

Horizontal symmetry-B.C.D.E.H.I.K.O.X.

Vertical symmetry-A.H.I.M.O.T.U.V.W.X.Y.

Roman numerals-C.D.I.L.M.V.X.

Just dots in Morse code-E.H.I.S. Just dashes in Morse code-M.O.T.

Horizontal and vertical symmetry-H.I.O.X.

Look the same upside down-H.I.N.O.S.X.Z.

Can be drawn in one stroke-B.C.D.G.I.J.L.M.N.O.P.R.S.U.V.W.Z.

Capitals which look like lowercase-C.O.P.S.U.V.W.X.Z.

 

 

THE ADVENTURE OF ENGLISH

THE BIOGRAPHY OF A LANGUAGE

Page 7

"Then came the great work, the laying of the foundations of the English language, and one which endures vigorously to this day.
Our everyday conversation is still founded on and funded by Old English. All of the following are Old English: is, you, man, son, daughter, friend, house, drink, here, there, the, in, on, intO, by, from, come, go, sheep, shepherd, ox, earth, home, horse, ground, plough, swine, mouse, dog, wood, field, work, eyes, ears, mouth, nose - 'my dog has no nose' - broth, fish, fowl, herring, love, lust, like, sing, glee, mirth, laughter, night, day, sun, word - 'come hell or high water'. These words are our foundation. We can have intelligent conversations in Old English and only rarely need we swerve away from it. Almost all of the hundred most common words in our language worldwide, wherever it is spoken, come from Old English. There are three from Old Norse, 'they', 'their' and 'them', and the first French-derived word is 'number', in at seventy-six.

The hundred words are:

1. the; 2. of; 3. and; 4. a; 5. to; 6. in; 7. is; 8. you; 9. that; lO. it; 11. he; 12. was; 13. for; 14. on; 15. are; 16. as; 17. with; 18. his; 19. they; 20. I; 21. at; 22. be; 23. this; 24. have; 25. from; 26. or; 27. one; 28. had; 29. by; 30. word; 31. but; 32. not; 33. what; 34. all; 35. were; 36. we; 37. when; 38. your; 39. can; 40. said; 41. there; 42. use; 43. an; 44. each; 45. which; 46. she; 47. do; 48. how; 49. their; 50. if; 51. will; 52. up; 53. other; 54. abour; 55. out; 56; many; 57. then; 58. them; 59. these; 60. so; 61. some; 62. her; 63. would; 64. make; 65. like; 66. him; 67. into; 68. time; 69. has; 70. look; 71. two; 72. more; 73. write; 74. go; 75. see; 76. number; 77. no; 78. way; 79. could; 80. people; 81. my; 82. than; 83. first; 84. water; 85. been; 86. call; 87. who; 88. oil; 89. its; 90. now; 91. find; 92. long; 93. down; 94. day; 95. did; 96. get; 97. come; 98. made; 99. may; 100. part."

 

 

1
T
=
2
-
3
THE
33
15
6
2
O
=
6
-
2
OF
21
12
3
3
A
=
1
-
3
AND
19
10
1
4
A
=
1
-
1
A
1
1
1
5
T
=
2
-
2
TO
35
8
8
6
I
=
9
-
2
IN
23
14
5
7
I
=
9
-
2
IS
28
10
1
8
Y
=
7
-
3
YOU
61
16
7
9
T
=
2
-
4
THAT
49
13
4
10
I
=
9
-
2
IT
29
11
2
11
H
=
8
-
2
HE
13
13
4
12
W
=
5
-
3
WAS
43
7
7
13
F
=
6
-
3
FOR
39
21
3
14
O
=
6
-
2
ON
29
11
2
15
A
=
1
-
3
ARE
24
15
6
16
A
=
1
-
2
AS
20
2
2
17
W
=
5
-
4
WITH
60
24
6
18
H
=
8
-
3
HIS
36
18
9
19
T
=
2
-
4
THEY
58
22
4
20
I
=
9
-
1
I
9
9
9
21
A
=
1
-
2
AT
21
3
3
22
B
=
2
-
2
BE
7
7
7
23
T
=
2
-
4
THIS
56
20
2
24
H
=
8
-
4
HAVE
36
18
9
25
F
=
6
-
4
FROM
52
25
7
26
O
=
6
-
2
OR
33
15
6
27
O
=
6
-
3
ONE
34
16
7
28
H
=
8
-
3
HAD
13
13
4
29
B
=
2
-
2
BY
27
9
9
30
W
=
5
-
4
WORD
60
24
6
31
B
=
2
-
3
BUT
43
7
7
32
N
=
5
-
3
NOT
49
13
4
33
W
=
5
-
4
WHAT
52
16
7
34
A
=
1
-
3
ALL
25
7
7
35
W
=
5
-
4
WERE
51
24
6
36
W
=
5
-
2
WE
28
10
1
37
W
=
5
-
4
WHEN
50
23
5
38
Y
=
7
-
4
YOUR
79
25
7
39
C
=
3
-
3
CAN
18
9
9
40
S
=
1
-
4
SAID
33
15
6
41
T
=
2
-
5
THERE
56
29
2
42
U
=
3
-
3
USE
45
9
9
43
A
=
1
-
2
AN
15
6
6
44
E
=
5
-
4
EACH
17
17
8
45
W
=
5
-
5
WHICH
51
33
6
46
S
=
1
-
3
SHE
32
14
5
47
D
=
4
-
2
DO
19
10
1
48
H
=
8
-
3
HOW
46
19
1
49
T
=
2
-
5
THEIR
60
33
6
50
I
=
9
-
2
IF
15
15
6
51
W
=
5
-
4
WILL
56
20
2
52
U
=
3
-
2
UP
37
10
1
53
O
=
6
-
5
OTHER
66
30
3
54
A
=
1
-
5
ABOUT
59
14
5
55
O
=
6
-
3
OUT
56
11
2
56
M
=
4
-
4
MANY
53
17
8
57
T
=
2
-
4
THEN
47
20
2
58
T
=
2
-
4
THEM
46
19
1
59
T
=
2
-
5
THESE
57
21
3
60
S
=
1
-
2
SO
34
7
7
61
S
=
1
-
4
SOME
52
16
7
62
H
=
8
-
3
HER
31
22
4
63
W
=
5
-
5
WOULD
75
21
3
64
M
=
4
-
4
MAKE
30
12
3
65
L
=
3
-
4
LIKE
37
19
1
66
H
=
8
-
3
HIM
30
21
3
67
I
=
9
-
4
INTO
58
22
4
68
T
=
2
-
4
TIME
47
20
2
69
H
=
8
-
3
HAS
28
10
1
70
L
=
3
-
4
LOOK
53
17
8
71
T
=
2
-
3
TWO
58
13
4
72
M
=
4
-
4
MORE
51
24
6
73
W
=
5
-
5
WRITE
75
30
3
74
G
=
7
-
2
GO
22
13
4
75
S
=
1
-
3
SEE
29
11
2
76
N
=
5
-
6
NUMBER
73
28
1
77
N
=
5
-
2
NO
29
11
2
78
W
=
5
-
3
WAY
49
13
4
79
C
=
3
-
5
COULD
55
19
1
80
P
=
7
-
6
PEOPLE
69
33
6
81
M
=
4
-
2
MY
38
11
2
82
T
=
2
-
4
THAN
43
16
7
83
F
=
6
-
5
FIRST
72
27
9
84
W
=
5
-
5
WATER
67
22
4
85
B
=
2
-
4
BEEN
26
17
8
86
C
=
3
-
4
CALL
28
10
1
87
W
=
5
-
3
WHO
46
19
1
88
O
=
6
3
3
OIL
36
18
9
89
I
=
9
-
3
ITS
48
12
3
90
N
=
5
-
3
NOW
52
16
7
91
F
=
6
-
4
FIND
33
24
6
92
L
=
3
-
4
LONG
48
21
3
93
D
=
4
-
4
DOWN
56
20
2
94
D
=
4
-
3
DAY
30
12
3
95
D
=
4
-
3
DID
17
17
8
96
G
=
7
-
3
GET
32
14
5
97
C
=
3
-
4
COME
36
18
9
98
M
=
4
-
4
MADE
23
14
5
99
M
=
4
-
3
MAY
39
12
3
100
P
=
7
-
4
PART
55
19
1
4860
-
-
634
-
336
-
4057
1618
457
4+8+6+0
-
-
6+3+4
-
3+3+6
-
4+0+5+7
1+6+1+8
4+5+7
18
-
-
13
-
12
-
16
16
16
1+8
-
-
1+3
-
1+2
-
1+6
1+6
1+6
9
-
-
4
-
3
-
7
7
7

 

 

1
T
=
2
-
3
THE
33
15
6
2
O
=
6
-
2
OF
21
12
3
3
A
=
1
-
3
AND
19
10
1
4
A
=
1
-
1
A
1
1
1
5
T
=
2
-
2
TO
35
8
8
6
I
=
9
-
2
IN
23
14
5
7
I
=
9
-
2
IS
28
10
1
8
Y
=
7
-
3
YOU
61
16
7
9
T
=
2
-
4
THAT
49
13
4
10
I
=
9
-
2
IT
29
11
2
11
H
=
8
-
2
HE
13
13
4
12
W
=
5
-
3
WAS
43
7
7
13
F
=
6
-
3
FOR
39
21
3
14
O
=
6
-
2
ON
29
11
2
15
A
=
1
-
3
ARE
24
15
6
16
A
=
1
-
2
AS
20
2
2
17
W
=
5
-
4
WITH
60
24
6
18
H
=
8
-
3
HIS
36
18
9
19
T
=
2
-
4
THEY
58
22
4
20
I
=
9
-
1
I
9
9
9
21
A
=
1
-
2
AT
21
3
3
22
B
=
2
-
2
BE
7
7
7
23
T
=
2
-
4
THIS
56
20
2
24
H
=
8
-
4
HAVE
36
18
9
25
F
=
6
-
4
FROM
52
25
7
26
O
=
6
-
2
OR
33
15
6
27
O
=
6
-
3
ONE
34
16
7
28
H
=
8
-
3
HAD
13
13
4
29
B
=
2
-
2
BY
27
9
9
30
W
=
5
-
4
WORD
60
24
6
31
B
=
2
-
3
BUT
43
7
7
32
N
=
5
-
3
NOT
49
13
4
33
W
=
5
-
4
WHAT
52
16
7
34
A
=
1
-
3
ALL
25
7
7
35
W
=
5
-
4
WERE
51
24
6
36
W
=
5
-
2
WE
28
10
1
37
W
=
5
-
4
WHEN
50
23
5
38
Y
=
7
-
4
YOUR
79
25
7
39
C
=
3
-
3
CAN
18
9
9
40
S
=
1
-
4
SAID
33
15
6
41
T
=
2
-
5
THERE
56
29
2
42
U
=
3
-
3
USE
45
9
9
43
A
=
1
-
2
AN
15
6
6
44
E
=
5
-
4
EACH
17
17
8
45
W
=
5
-
5
WHICH
51
33
6
46
S
=
1
-
3
SHE
32
14
5
47
D
=
4
-
2
DO
19
10
1
48
H
=
8
-
3
HOW
46
19
1
49
T
=
2
-
5
THEIR
60
33
6
50
I
=
9
-
2
IF
15
15
6
51
W
=
5
-
4
WILL
56
20
2
52
U
=
3
-
2
UP
37
10
1
53
O
=
6
-
5
OTHER
66
30
3
54
A
=
1
-
5
ABOUT
59
14
5
55
O
=
6
-
3
OUT
56
11
2
56
M
=
4
-
4
MANY
53
17
8
57
T
=
2
-
4
THEN
47
20
2
58
T
=
2
-
4
THEM
46
19
1
59
T
=
2
-
5
THESE
57
21
3
60
S
=
1
-
2
SO
34
7
7
61
S
=
1
-
4
SOME
52
16
7
62
H
=
8
-
3
HER
31
22
4
63
W
=
5
-
5
WOULD
75
21
3
64
M
=
4
-
4
MAKE
30
12
3
65
L
=
3
-
4
LIKE
37
19
1
66
H
=
8
-
3
HIM
30
21
3
67
I
=
9
-
4
INTO
58
22
4
68
T
=
2
-
4
TIME
47
20
2
69
H
=
8
-
3
HAS
28
10
1
70
L
=
3
-
4
LOOK
53
17
8
71
T
=
2
-
3
TWO
58
13
4
72
M
=
4
-
4
MORE
51
24
6
73
W
=
5
-
5
WRITE
75
30
3
74
G
=
7
-
2
GO
22
13
4
75
S
=
1
-
3
SEE
29
11
2
76
N
=
5
-
6
NUMBER
73
28
1
77
N
=
5
-
2
NO
29
11
2
78
W
=
5
-
3
WAY
49
13
4
79
C
=
3
-
5
COULD
55
19
1
80
P
=
7
-
6
PEOPLE
69
33
6
81
M
=
4
-
2
MY
38
11
2
82
T
=
2
-
4
THAN
43
16
7
83
F
=
6
-
5
FIRST
72
27
9
84
W
=
5
-
5
WATER
67
22
4
85
B
=
2
-
4
BEEN
26
17
8
86
C
=
3
-
4
CALL
28
10
1
87
W
=
5
-
3
WHO
46
19
1
88
O
=
6
3
3
OIL
36
18
9
89
I
=
9
-
3
ITS
48
12
3
90
N
=
5
-
3
NOW
52
16
7
91
F
=
6
-
4
FIND
33
24
6
92
L
=
3
-
4
LONG
48
21
3
93
D
=
4
-
4
DOWN
56
20
2
94
D
=
4
-
3
DAY
30
12
3
95
D
=
4
-
3
DID
17
17
8
96
G
=
7
-
3
GET
32
14
5
97
C
=
3
-
4
COME
36
18
9
98
M
=
4
-
4
MADE
23
14
5
99
M
=
4
-
3
MAY
39
12
3
4760
-
-
627
-
332
-
4002
1599
456
4+7+6+0
-
-
6+2+7
-
3+3+2
-
4+0+0+2
1+5+9+9
4+5+6
17
-
-
15
-
8
-
6
24
15
1+7
--
1
1+5
-
-
-
-
2+4
1+5
8
-
-
6
-
8
-
6
6
6

 

 

ANTIDISESTABLISHMENTARIANISM

 

A
=
1
-
3
ANT
35
8
8
-
=
-
-
1
I
9
9
9
-
=
-
-
1
D
4
4
4
-
=
-
-
1
I
9
9
9
-
=
-
-
4
SEST
63
9
9
-
=
-
-
3
ABL
15
6
6
-
=
-
-
1
I
9
9
9
-
=
-
-
2
SH
27
9
9
-
=
-
-
2
ME
18
9
9
-
=
-
-
3
NTA
35
8
8
-
=
-
-
1
R
18
9
9
-
=
-
-
1
I
9
9
9
-
=
-
-
2
AN
15
6
6
-
=
-
-
1
I
9
9
9
-
=
-
-
2
SM
32
5
5
-
-
1
4
28
First Total
307
118
118
-
-
-
-
2+8
Add to Reduce
3+0+7
1+1+8
1+1+8
-
-
1
=
10
Second Total
10
10
10
-
-
-
-
1+0
Reduce to Deduce
1+0
1+0
1+0
-
-
1
-
1
Essence of Number
1
1
1

 

ANTIDISESTABLISHMENTARIANISM

 

28
A
N
T
I
D
I
S
E
S
T
A
B
L
I
S
H
M
E
N
T
A
R
I
A
N
I
S
M
-
-
-
-
-
-
-
-
-
-
-
-
5
-
9
-
9
1
-
1
-
-
-
-
9
1
8
-
-
5
-
-
-
9
-
5
9
1
-
+
=
43
4+3
=
7
=
7
=
7
-
-
14
-
9
-
9
19
-
19
-
-
-
-
9
19
8
-
-
14
-
-
-
9
-
14
9
19
-
+
=
115
1+1+5
=
7
=
7
=
7
28
A
N
T
I
D
I
S
E
S
T
A
B
L
I
S
H
M
E
N
T
A
R
I
A
N
I
S
M
-
-
-
-
-
-
-
-
-
-
-
1
-
2
-
4
-
-
5
-
2
1
2
3
-
-
-
4
5
-
2
1
9
-
1
-
-
-
4
+
=
83
8+3
=
11
1+1
2
=
2
-
1
-
20
-
4
-
-
5
-
20
1
2
12
-
-
-
13
5
-
20
1
18
-
1
-
-
-
13
+
=
236
2+3+6
=
11
1+1
2
=
2
28
A
N
T
I
D
I
S
E
S
T
A
B
L
I
S
H
M
E
N
T
A
R
I
A
N
I
S
M
-
-
-
-
-
-
-
-
-
-
-
1
14
20
9
4
9
19
5
19
20
1
2
12
9
19
8
13
5
14
20
1
18
9
1
14
9
19
13
+
=
307
3+0+7
=
10
1+0
1
=
1
-
1
5
2
9
4
9
1
5
1
2
1
2
3
9
1
8
4
5
5
2
1
9
9
1
5
9
1
4
+
=
118
1+1+8
=
10
1+0
1
=
1
28
A
N
T
I
D
I
S
E
S
T
A
B
L
I
S
H
M
E
N
T
A
R
I
A
N
I
S
M
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
1
-
1
-
1
-
-
-
1
-
-
-
-
-
1
-
-
1
-
-
1
-
+
=
1
occurs
x
8
=
8
=
8
-
-
-
2
-
-
-
-
-
-
2
-
2
-
-
-
-
-
-
-
2
-
-
-
-
-
-
-
-
+
=
2
occurs
x
4
=
8
=
8
-
-
-
-
-
-
-
-
-
-
-
-
-
3
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
+
=
3
occurs
x
1
=
3
=
3
-
-
-
-
-
4
-
-
-
-
-
-
-
-
-
-
-
4
-
-
-
-
-
-
-
-
-
-
4
+
=
4
occurs
x
3
=
12
1+2
3
-
-
5
-
-
-
-
-
5
-
-
-
-
-
-
-
-
-
5
5
-
-
-
-
-
5
-
-
-
+
=
5
occurs
x
5
=
25
2+5
7
6
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
+
=
6
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
+
=
7
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
-
-
-
-
+
=
8
occurs
x
1
=
8
=
8
-
-
-
-
9
-
9
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
9
9
-
-
9
-
-
+
=
9
occurs
x
6
=
54
5+4
9
13
A
N
T
I
D
I
S
E
S
T
A
B
L
I
S
H
M
E
N
T
A
R
I
A
N
I
S
M
-
-
45
-
-
26
-
118
-
46
-
1
-
-
-
-
-
1
-
1
-
1
-
-
-
1
-
-
-
-
-
1
-
-
1
-
-
1
-
-
-
4+5
-
-
2+6
-
1+1+8
-
4+6
13
A
N
T
I
D
I
S
E
S
T
A
B
L
I
S
H
M
E
N
T
A
R
I
A
N
I
S
M
-
-
9
-
-
8
-
10
-
10
-
1
5
2
9
4
9
1
5
1
2
1
2
3
9
1
8
4
5
5
2
1
9
9
1
5
9
1
4
-
-
-
-
-
-
-
1+0
-
1+0
13
A
N
T
I
D
I
S
E
S
T
A
B
L
I
S
H
M
E
N
T
A
R
I
A
N
I
S
M
-
-
9
-
-
8
-
1
-
1

 

 

What is a 'neener' - WikiAnswers

wiki.answers.com › ... › Idioms, Cliches, and Slang

Meaning of 'Neener' Neener Neener is an expression that most Americans aged 40 or under are probably familiar with. Following is a typical example of usage: ...

 

Where does "neener neener neener" come from? - Straight Dope ...

boards.straightdope.com › ... › Main › General Questions

28 Nov 2000 - 12 posts - ‎10 authors
You all know the song. "neener neener neener" This melody usually has improvised lyrics, aimed at the subject of some ridicule. But where ...

 

neener - Wiktionary

en.wiktionary.org/wiki/neener

Grizzy shouted. She ran up to some old Grouch ladies. She stuck her tongue out at them. She blew a great big razzberry at them. "Neener, neener, neener!"...linguaphiles: Neener-neener

 

 

linguaphiles.livejournal.com/1509243.html

28 Mar 2005 - Is the childhood taunt 'neener-neener' always considered an insult, or is there a use that's not an insult? Any ideas about its origins? Thanks.

 

 

neener, neener, pumpkin eater - definition and meaning

https://www.wordnik.com/.../neener,%20neener,%20pumpkin%20eater

neener, neener, pumpkin eater. Define; Relate; List; Discuss ... These user-created lists contain the word 'neener, neener, pumpkin eater'. Nyah, nyah, nyah.

 

Dubya Pee'z Geekology Cogitation Manual

books.google.co.uk/books?isbn=1456729314 Robert Tracy - 2011 - ‎Fiction
Double yellow lines mid-road reside multiple instances directly underneath ancient Voreign hot rod belly sections. 32... “NEENER NEENER NEENER NEENER"

 

 

-
18
N
E
E
N
E
R
-
N
E
E
N
E
R
-
N
E
E
N
E
R
-
-
-
-
-
-
-
-
-
-
-
-
-
-
5
-
-
5
-
-
-
5
-
-
5
-
-
-
5
-
-
5
-
-
+
=
30
3+0
=
3
=
3
=
3
=
3
-
-
14
-
-
14
-
-
-
14
-
-
14
-
-
-
14
-
-
14
-
-
+
=
84
8+4
=
12
1+2
3
=
3
=
3
-
18
N
E
E
N
E
R
-
N
E
E
N
E
R
-
N
E
E
N
E
R
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
5
5
-
5
9
-
-
5
5
-
5
9
-
-
5
5
-
5
9
+
=
72
7+2
=
9
=
9
=
9
=
9
-
-
-
5
5
-
5
18
-
-
5
5
-
5
18
-
-
5
5
-
5
18
+
=
99
9+9
=
18
1+8
9
=
9
=
9
-
18
N
E
E
N
E
R
-
N
E
E
N
E
R
-
N
E
E
N
E
R
-
-
-
-
-
-
-
-
-
-
-
-
-
-
14
5
5
14
5
18
-
14
5
5
14
5
18
-
14
5
5
14
5
18
+
=
183
1+8+3
=
12
1+2
3
=
3
=
3
-
-
5
5
5
5
5
9
-
5
5
5
5
5
9
-
5
5
5
5
5
9
+
=
102
1+0+2
=
3
=
3
=
3
=
3
-
18
N
E
E
N
E
R
-
N
E
E
N
E
R
-
N
E
E
N
E
R
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
ONE
1
-
-
-
-
-
-
-
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
2
TWO
2
-
-
-
-
-
-
-
3
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
3
THREE
3
-
-
-
-
-
-
-
4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
4
FOUR
4
-
-
-
-
-
-
-
-
-
5
5
5
5
5
-
-
5
5
5
5
5
-
-
5
5
5
5
5
-
-
-
5
occurs
x
15
=
75
7+5
12
1+2
3
6
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
6
SIX
6
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
7
SEVEN
7
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
8
EIGHT
8
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
9
-
-
-
-
-
-
9
-
-
9
occurs
x
3
=
27
2+7
9
-
9
31
18
N
E
E
N
E
R
-
N
E
E
N
E
R
-
N
E
E
N
E
R
-
-
14
-
-
13
-
102
-
21
-
12
3+1
1+8
5
5
5
5
5
-
-
5
5
5
5
5
-
-
5
5
5
5
5
-
-
-
1+4
-
-
1+3
-
1+1
-
2+1
-
1+2
4
9
N
E
E
N
E
R
-
N
E
E
N
E
R
-
N
E
E
N
E
R
-
-
5
-
-
4
-
8
-
3
-
3
-
-
5
5
5
5
5
9
-
5
5
5
5
5
9
-
5
5
5
5
5
9
-
-
-
-
-
-
-
-
-
-
-
-
4
9
N
E
E
N
E
R
-
N
E
E
N
E
R
-
N
E
E
N
E
R
-
-
5
-
-
4
-
8
-
3
-
3

 

 

-
VOWEL
-
-
-
1
V
22
4
4
1
O
15
6
6
1
W
23
5
5
1
E
5
5
5
1
L
12
3
3
5
VOWEL
77
23
23
-
-
1+4
2+3
2+3
5
VOWEL
5
5
5

 

 

-
VOWELS
-
-
-
1
V
22
4
4
1
O
15
6
6
1
W
23
5
5
1
E
5
5
5
1
L
12
3
3
1
S
19
10
1
6
VOWELS
96
33
24
-
-
9+6
3+3
2+4
6
VOWELS
15
6
6
-
-
1+5
-
-
6
VOWELS
6
6
6

 

 

-
A E I O U
-
-
-
1
A
1
1
1
1
E
5
5
5
1
I
9
9
9
1
O
15
6
6
1
U
21
3
3
5
A E I O U
51
24
24
-
-
5+1
2+4
2+4
5
A E I O U
6
6
6

 

 

-
5
A
-
E
-
I
-
O
-
U
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
-
6
-
-
+
=
15
1+5
=
6
=
6
-
-
-
-
-
-
9
-
15
-
-
+
=
24
2+4
=
6
=
6
-
5
A
-
E
-
I
-
O
-
U
-
-
-
-
-
-
-
-
-
-
1
-
5
-
-
-
-
-
3
+
=
9
-
=
9
=
9
-
-
1
-
5
-
-
-
-
-
21
+
=
27
2+7
=
9
=
9
-
5
A
-
E
-
I
-
O
-
U
-
-
-
-
-
-
-
-
-
-
1
-
5
-
9
-
15
-
21
+
=
51
5+1
=
6
=
6
-
-
1
-
5
-
9
-
6
-
3
+
=
24
2+4
=
6
=
6
-
5
A
-
E
-
I
-
O
-
U
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
-
-
1
occurs
x
1
=
1
2
-
-
-
-
-
-
-
-
-
-
-
-
2
TWO
2
-
-
-
-
-
-
-
-
-
-
-
-
-
3
-
-
3
occurs
x
1
=
3
4
-
-
-
-
-
-
-
-
-
-
-
-
4
FOUR
4
-
-
-
-
-
-
-
5
-
-
-
-
-
-
-
-
5
occurs
x
1
=
5
-
-
-
-
-
-
-
-
6
-
-
-
-
6
occurs
x
1
=
6
7
-
-
-
-
-
-
-
-
-
-
-
-
7
SEVEN
7
-
-
-
8
-
-
-
-
-
-
-
-
-
-
-
-
8
EIGHT
8
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
9
occurs
x
1
=
9
21
5
A
-
E
-
I
-
O
-
U
-
-
24
-
-
5
-
24
2+1
-
-
-
-
-
9
-
-
-
-
-
-
2+4
-
-
-
-
2+4
3
5
A
-
E
-
I
-
O
-
U
-
-
6
-
-
5
-
6
-
-
1
-
5
-
9
-
6
-
3
-
-
-
-
-
-
-
-
3
5
A
-
E
-
I
-
O
-
U
-
-
6
-
-
5
-
6

 

 

5
A
-
E
-
I
-
O
-
U
-
-
-
-
-
-
-
-
-
-
-
-
-
9
-
6
-
-
+
=
15
1+5
=
6
=
6
-
-
-
-
-
9
-
15
-
-
+
=
24
2+4
=
6
=
6
5
A
-
E
-
I
-
O
-
U
-
-
-
-
-
-
-
-
-
1
-
5
-
-
-
-
-
3
+
=
9
-
=
9
=
9
-
1
-
5
-
-
-
-
-
21
+
=
27
2+7
=
9
=
9
5
A
-
E
-
I
-
O
-
U
-
-
-
-
-
-
-
-
-
1
-
5
-
9
-
15
-
21
+
=
51
5+1
=
6
=
6
-
1
-
5
-
9
-
6
-
3
+
=
24
2+4
=
6
=
6
5
A
-
E
-
I
-
O
-
U
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
-
-
1
occurs
x
1
=
1
-
-
-
-
-
-
-
-
-
3
-
-
3
occurs
x
1
=
3
-
-
-
5
-
-
-
-
-
-
-
-
5
occurs
x
1
=
5
-
-
-
-
-
-
-
6
-
-
-
-
6
occurs
x
1
=
6
-
-
-
-
-
9
-
-
-
-
-
-
9
occurs
x
1
=
9
5
A
-
E
-
I
-
O
-
U
-
-
24
-
-
5
-
24
-
-
-
-
-
9
-
-
-
-
-
-
2+4
-
-
-
-
2+4
5
A
-
E
-
I
-
O
-
U
-
-
6
-
-
5
-
6
-
1
-
5
-
9
-
6
-
3
-
-
-
-
-
-
-
-
5
A
-
E
-
I
-
O
-
U
-
-
6
-
-
5
-
6

 

 

5
A
E
I
O
U
-
-
-
-
-
-
-
-
-
-
-
9
6
-
+
=
15
1+5
=
6
=
6
-
-
-
9
15
-
+
=
24
2+4
=
6
=
6
5
A
E
I
O
U
-
-
-
-
-
-
-
-
-
1
5
-
-
3
+
=
9
-
=
9
=
9
-
1
5
-
-
21
+
=
27
2+7
=
9
=
9
5
A
E
I
O
U
-
-
-
-
-
-
-
-
-
1
5
9
15
21
+
=
51
5+1
=
6
=
6
-
1
5
9
6
3
+
=
24
2+4
=
6
=
6
5
A
E
I
O
U
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
1
occurs
x
1
=
1
-
-
-
-
-
3
-
-
3
occurs
x
1
=
3
-
-
5
-
-
-
-
-
5
occurs
x
1
=
5
-
-
-
-
6
-
-
-
6
occurs
x
1
=
6
-
-
-
9
-
-
-
-
9
occurs
x
1
=
9
5
A
E
I
O
U
-
-
24
-
-
5
-
24
-
-
-
9
-
-
-
-
2+4
-
-
-
-
2+4
5
A
E
I
O
U
-
-
6
-
-
5
-
6
-
1
5
9
6
3
-
-
-
-
-
-
-
-
5
A
E
I
O
U
-
-
6
-
-
5
-
6

 

 

-
CONSONANT
-
-
-
1
C
3
3
3
1
O
15
6
6
1
N
14
5
5
1
S
19
10
1
1
O
15
6
6
1
N
14
5
5
1
A
1
1
1
1
N
14
5
5
1
T
20
2
2
9
CONSONANT
115
43
34
-
-
1+1+5
4+3
3+4
9
CONSONANT
7
7
7

 

 

-
CONSONANTS
-
-
-
1
C
3
3
3
1
O
15
6
6
1
N
14
5
5
1
S
19
10
1
1
O
15
6
6
1
N
14
5
5
1
A
1
1
1
1
N
14
5
5
1
T
20
2
2
1
S
19
10
1
10
CONSONANTS
134
53
35
3+4
-
1+3+4
5+3
3+5
7
CONSONANTS
8
8
8

 

 

5
VOWEL
77
23
5
6
VOWELS
96
33
6
-
-
-
--
--
-
-
-
--
--
9
CONSONANT
115
43
34
10
CONSONANTS
134
53
35

 

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

 

-
ENGLISH
-
-
-
4
E+N+G+L
38
20
2
3
I+S+H
36
18
9
7
ENGLISH
74
38
11
-
-
7+4
3+9
1+1
7
ENGLISH
11
11
2
-
-
1+1
1+1
-
7
ENGLISH
2
2
2

 

 

Daily Mail

Thursday, June 11 2009

Page 37

Web 2.0 - the one millionth English word

ALMOST 1,500 years after it was first recorded, the English language has its one millionth word.

At 10.22am yesterday Web 2.0 - describing the next generation of internet services entered the dictionary.

To be accepted a word must be used at least 25,000 times across national boundaries and outside specialisms.

U.S-based Global Language Monitor surveys print publications, online news sites, blogs and social media for useage.

Jai Ho!, a Hindi phrase signifying the joy of victory became the 999,999th word thanks to the Oscar-Winning film Slumdog millionaire.

At 1,000,001 is Financial Tsunami - a sudden financial restructuring.

 

 

"JAI HO! A HINDI PHRASE SIGNIFYING THE JOY OF VICTORY BECAME THE 999,999TH WORD..."

 

 

3
THE
33
15
6
7
ENGLISH
74
38
2
8
LANGUAGE
68
32
5
18
175
85
13
1+8
1+7+5
8+5
1+3
9
13
13
4
8
THIRTEEN
99
45
9

 

 

7
ENGLISH
74
38
2
8
LANGUAGE
68
32
5
15
First Total
142
79
7
1+5
Add to Reduce
1+4+2
7+9
-
6
Second Total
7
16
7
-
Reduce to Deduce
-
1+6
-
6
Essence of Number
7
7
7

 

 

 

O
=
6
-
3
OUT
56
11
2
O
=
6
-
2
OF
21
12
3
Z
=
8
-
4
ZERO
64
28
1
C
=
3
-
6
COMETH
64
28
1
O
=
6
-
3
ONE
34
16
7
Q
Q
29
Q
18
Q
239
95
14
-
-
2+9
-
1+8
-
2+3+9
9+5
1+4
-
-
11
-
9
-
14
14
5
-
-
1+1
-
-
-
1+4
1+4
-
-
-
2
-
9
-
5
5
5

 

 

THERE IS NO ATTEMPT MADE TO DESCRIBE THE CREATIVE PROCESS REALISTICALLY

THE ACCOUNT IS SYMBOLIC AND SHOWS GOD CREATING THE WORLD BY MEANS OF LANGUAGE

AS THOUGH WRITING A BOOK BUT LANGUAGE ENTIRELY TRANSFORMED

THE MESSAGE OF CREATION IS CLEAR EACH LETTER OF

THE

ALPHABET

IS

GIVEN

A

NUMERICAL

VALUE BY COMBINING THE LETTERS WITH THE SACRED NUMBERS

REARRANGING THEM IN ENDLESS CONFIGURATIONS

THE MYSTIC WEANED THE MIND AWAY FROM THE NORMAL CONNOTATIONS OF WORDS

 

....

 

THE LIGHT IS RISING RISING IS THE LIGHT

 

 

9
LANGUAGES
87
33
6
3
AND
19
10
1
7
NUMBERS
92
29
2
19
-
198
72
9
1+9
-
1+9+8
7+2
-
10
-
18
9
9
1+0
-
1+8
-
-
1
-
9
9
9

 

 

L
=
3
-
8
LANGUAGE
68
32
5
T
=
2
-
7
TALKING
74
29
2
N
=
5
-
7
NUMBERS
92
29
2
-
=
10
-
22
-
234
90
9
-
=
1+0
-
2+2
-
2+3+4
9+0
-
-
=
1
-
4
-
9
9
9

 

 

T
=
2
-
9
THE
33
15
6
E
=
5
-
3
ENGLISH
74
29
2
A
=
1
-
7
ALPHABET
65
29
2
-
-
8
-
19
-
172
73
10
-
-
4+6
-
1+9
-
1+7+2
7+3
1+0
-
-
8
-
10
-
10
10
1
-
-
-
-
1+0
-
1+0
1+0
-
-
-
8
-
1
-
1
1
1

 

 

-
-
-
-
-
LANGUAGE
-
-
-
L
=
3
-
2
L+A+N
27
9
9
A
=
1
-
2
G+U+A+G
18
18
9
N
=
5
-
3
E
5
5
5
-
-
32
-
8
LANGUAGE
68
32
32
-
-
3+2
-
-
-
6+8
3+2
3+2
-
-
5
-
8
LANGUAGE
14
5
5
-
-
-
-
-
-
1+4
-
-
-
-
5
-
8
LANGUAGE
5
5
5

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
LANGUAGE
-
-
-
-
-
-
-
-
-
-
-
-
-
L
=
3
-
2
L
12
3
3
-
-
-
3
-
-
-
-
-
-
A
=
1
-
2
A
1
1
1
-
1
-
-
-
-
-
-
-
-
N
=
5
-
3
N
14
5
5
-
-
-
-
-
5
-
-
-
-
G
=
7
-
2
G
7
7
7
-
-
-
-
-
-
-
7
-
-
U
=
3
-
3
U
21
3
3
-
-
-
3
-
-
-
-
-
-
A
=
1
-
3
A
1
1
1
-
1
-
-
-
-
-
-
-
-
G
=
7
-
4
G
7
7
7
-
-
-
-
-
-
-
7
-
-
E
=
5
-
3
E
5
5
5
-
-
-
-
-
5
-
-
-
-
-
-
32
-
8
LANGUAGE
68
32
32
-
2
2
6
4
10
6
14
8
9
-
-
3+2
-
-
-
6+8
3+2
3+2
-
-
-
-
-
1+0
-
1+4
-
-
-
-
5
-
8
LANGUAGE
14
5
5
-
2
2
6
4
1
6
5
8
9
-
-
-
-
-
-
1+4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
5
-
8
LANGUAGE
5
5
5
-
2
2
6
4
1
6
5
8
9

 

 

LAND

ENGAGE LAND ENGAGE

 

 

BBC - Languages - Languages - Languages of the world ...

www.bbc.co.uk/languages/guide/languages.shtml‎

Languages of the world. A guide to which languages are most widely spoken, hardest to learn and other revealing facts. Open/close. 1. How many languages ...

It’s estimated that up to 7,000 different languages are spoken around the world. 90% of these languages are used by less than 100,000 people. Over a million people converse in 150-200 languages and 46 languages have just a single speaker!

Languages are grouped into families that share a common ancestry. For example, English is related to German and Dutch, and they are all part of the Indo-European family of languages. These also include Romance languages, such as French, Spanish and Italian, which come from Latin.

2,200 of the world’s languages can be found in Asia, while Europe has a mere 260.

Nearly every language uses a similar grammatical structure, even though they may not be linked in vocabulary or origin. Communities which are usually isolated from each other because of mountainous geography may have developed multiple languages. Papua New Guinea for instance, boasts no less than 832 different languages!

 


Exactly How Many Languages Are There in the World?

www.translationblog.co.uk/exactly-how-many-languages-are-there-in-th...‎

Jan 11, 2010 – One of the challenges we face as a language solutions provider is covering demand for the languages that our clients request on a daily basis.

RichardLoyer | January 11, 2010

Exactly How Many Languages Are There in the World?


One of the challenges we face as a language solutions provider is covering demand for the languages that our clients request on a daily basis. So how many languages are there in the World and how do we go about providing translation and interpreting in all of them….?

The invaluable Ethnologue quotes 6909 living languages, that’s one language for every 862,000 people on Earth. Let’s look at some more figures from Ethnologue’s database.

Europe, with ¼ of the World’s population has only 234 languages spoken on a daily basis.

Although English does well as the World’s business language-at least for the time being- it is only 3rd in the league table of native speakers of a first language, with 328M, only 1m behind Spanish but a long way from the 845M Mandarin speakers.

94% of languages are spoken by only 6% of the World’s population, which tells us that there are hundreds of languages with just a few thousand [or hundred] speakers.

Many of these languages would be classified by some as dialects i.e. languages that have evolved from but are still quite closely related to another. This definition, of course, falls down very rapidly as most Western European languages can trace their roots to Latin but would not normally be described as dialects. Some of the African and Caribbean Patois are still seen as dialects, as was Ulster-Scots until fairly recently when it was recognised as a language. http://www.ulsterscotsagency.com/

The most famous phrase “a language is a dialect with an army and a navy” is wrongly attributed to Yiddish scholar Max Weinreich, who was probably quoting an anonymous teacher from New York, but it is a neat way to make the definition.

So how many of these languages are regularly translated by Applied Language? Well, it’s a lot but not quite 6909…….we reckon that about 200 languages are translated regularly by our global offices into documents, websites, brochures and anything else you can imagine. The range of languages required by our interpreting team is rather smaller at about 100.

The difference is no mystery; companies that translate their promotional material may be selling into every part of the globe and therefore their need is very broad whilst a hospital in Manchester, for example, will only have to deal with the resident non-native speakers and unwell tourists that come through its doors. Although the interpreting requirement is significant, it rarely exceeds 100 different languages.

Some of the most difficult requests are for languages that unfortunately don’t exist; enquiries for “Indian” or “Eastern European” do pop up occasionally. Similarly, “African” or “South American” can have us scratching our heads.

As a final thought for those of you currently learning another language you might be slightly discouraged by a report from Swarthmore College linguist K. David Harrison who predicts that 90% of the World’s languages will be extinct by 2050. http://www.msnbc.msn.com/id/4387421/

This might make finding translators a little easier, but would surely make our World a rather less interesting place?

 

 

Alphabet - Wikipedia, the free encyclopedia

en.wikipedia.org/wiki/Alphabet‎

An alphabet is a standard set of letters (basic written symbols or graphemes) which is used to write one or more languages based on the general principle that ...

Alphabet

From Wikipedia, the free encyclopedia

Jump to: navigation, search

This article is about sets of letters used in written languages. For other uses, see Alphabet (disambiguation).

An alphabet is a standard set of letters (basic written symbols or graphemes) which is used to write one or more languages based on the general principle that the letters represent phonemes (basic significant sounds) of the spoken language. This is in contrast to other types of writing systems, such as syllabaries (in which each character represents a syllable) and logographies (in which each character represents a word, morpheme or semantic unit).

A true alphabet has letters for the vowels of a language as well as the consonants. The first "true alphabet" in this sense is believed to be the Greek alphabet,[1][2] which is a modified form of the Phoenician alphabet. In other types of alphabet either the vowels are not indicated at all, as was the case in the Phoenician alphabet (such systems are known as abjads), or else the vowels are shown by diacritics or modification of consonants, as in the devanagari used in India and Nepal (these systems are known as abugidas or alphasyllabaries).

There are dozens of alphabets in use today, the most popular being the Latin alphabet[3] (which was derived from the Greek). Many languages use modified forms of the Latin alphabet, with additional letters formed using diacritical marks. While most alphabets have letters composed of lines (linear writing), there are also exceptions such as the alphabets used in Braille, fingerspelling, and Morse code.

Alphabets are usually associated with a standard ordering of their letters. This makes them useful for purposes of collation, specifically by allowing words to be sorted in alphabetical order. It also means that their letters can be used as an alternative method of "numbering" ordered items, in such contexts as numbered lists.

Contents
[hide] 1 Etymology
2 History 2.1 Middle Eastern scripts
2.2 European alphabets
2.3 Asian alphabets

3 Types
4 Alphabetical order
5 Names of letters
6 Orthography and pronunciation
7 See also
8 References
9 Bibliography
10 External links

Etymology[edit]

The English word alphabet came into Middle English from the Late Latin word alphabetum, which in turn originated in the Greek ἀλφάβητος (alphabētos), from alpha and beta, the first two letters of the Greek alphabet.[4] Alpha and beta in turn came from the first two letters of the Phoenician alphabet, and originally meant ox and house respectively.

History[edit]

Main article: History of the alphabet

A Specimen of typeset fonts and languages, by William Caslon, letter founder; from the 1728 Cyclopaedia.
Middle Eastern scripts[edit]

The history of the alphabet started in ancient Egypt. By the 27th century BC Egyptian writing had a set of some 24 hieroglyphs which are called uniliterals,[5] to represent syllables that begin with a single consonant of their language, plus a vowel (or no vowel) to be supplied by the native speaker. These glyphs were used as pronunciation guides for logograms, to write grammatical inflections, and, later, to transcribe loan words and foreign names.[6]

A specimen of Proto-Sinaitic script, one of the earliest (if not the very first) phonemic scripts
In the Middle Bronze Age an apparently "alphabetic" system known as the Proto-Sinaitic script appears in Egyptian turquoise mines in the Sinai peninsula dated to circa the 15th century BC, apparently left by Canaanite workers. In 1999, John and Deborah Darnell discovered an even earlier version of this first alphabet at Wadi el-Hol dated to circa 1800 BC and showing evidence of having been adapted from specific forms of Egyptian hieroglyphs that could be dated to circa 2000 BC, strongly suggesting that the first alphabet had been developed circa that time.[7] Based on letter appearances and names, it is believed to be based on Egyptian hieroglyphs.[8] This script had no characters representing vowels. An alphabetic cuneiform script with 30 signs including three which indicate the following vowel was invented in Ugarit before the 15th century BC. This script was not used after the destruction of Ugarit.[9]

The Proto-Sinaitic script eventually developed into the Phoenician alphabet, which is conventionally called "Proto-Canaanite" before ca. 1050 BC.[10] The oldest text in Phoenician script is an inscription on the sarcophagus of King Ahiram. This script is the parent script of all western alphabets. By the tenth century two other forms can be distinguished namely Canaanite and Aramaic. The Aramaic gave rise to Hebrew.[11] The South Arabian alphabet, a sister script to the Phoenician alphabet, is the script from which the Ge'ez alphabet (an abugida) is descended. Vowelless alphabets, which are not true alphabets, are called abjads, currently exemplified in scripts including Arabic, Hebrew, and Syriac. The omission of vowels was not a satisfactory solution and some "weak" consonants were used to indicate the vowel quality of a syllable (matres lectionis). These had dual function since they were also used as pure consonants.[12]

The Proto-Sinatic or Proto Canaanite script and the Ugaritic script were the first scripts with limited number of signs, in contrast to the other widely used writing systems at the time, Cuneiform, Egyptian hieroglyphs, and Linear B. The Phoenician script was probably the first phonemic script[8][10] and it contained only about two dozen distinct letters, making it a script simple enough for common traders to learn. Another advantage of Phoenician was that it could be used to write down many different languages, since it recorded words phonemically.

The script was spread by the Phoenicians, across the Mediterranean.[10] In Greece, the script was modified to add the vowels, giving rise to the ancestor of all alphabets in the West. The indication of the vowels is the same way as the indication of the consonants, therefore it was the first true alphabet. The Greeks took letters which did not represent sounds that existed in Greek, and changed them to represent the vowels. The vowels are significant in the Greek language, and the syllabical Linear B script which was used by the Mycenaean Greeks from the 16th century BC had 87 symbols including 5 vowels. In its early years, there were many variants of the Greek alphabet, a situation which caused many different alphabets to evolve from it.

European alphabets[edit]

Codex Zographensis in the Glagolitic alphabet from Medieval Bulgaria
The Greek alphabet, in its Euboean form, was carried over by Greek colonists to the Italian peninsula, where it gave rise to a variety of alphabets used to write the Italic languages. One of these became the Latin alphabet, which was spread across Europe as the Romans expanded their empire. Even after the fall of the Roman state, the alphabet survived in intellectual and religious works. It eventually became used for the descendant languages of Latin (the Romance languages) and then for most of the other languages of Europe.

Some adaptations of the Latin alphabet are augmented with ligatures, such as æ in Old English and Icelandic and Ȣ in Algonquian; by borrowings from other alphabets, such as the thorn þ in Old English and Icelandic, which came from the Futhark runes; and by modifying existing letters, such as the eth ð of Old English and Icelandic, which is a modified d. Other alphabets only use a subset of the Latin alphabet, such as Hawaiian, and Italian, which uses the letters j, k, x, y and w only in foreign words.

Another notable script is Elder Futhark, which is believed to have evolved out of one of the Old Italic alphabets. Elder Futhark gave rise to a variety of alphabets known collectively as the Runic alphabets. The Runic alphabets were used for Germanic languages from AD 100 to the late Middle Ages. Its usage is mostly restricted to engravings on stone and jewelry, although inscriptions have also been found on bone and wood. These alphabets have since been replaced with the Latin alphabet, except for decorative usage for which the runes remained in use until the 20th century.

The Old Hungarian script is a contemporary writing system of the Hungarians. It was in use during the entire history of Hungary, albeit not as an official writing system. From the 19th century it once again became more and more popular.

The Glagolitic alphabet was the initial script of the liturgical language Old Church Slavonic and became, together with the Greek uncial script, the basis of the Cyrillic script. Cyrillic is one of the most widely used modern alphabetic scripts, and is notable for its use in Slavic languages and also for other languages within the former Soviet Union. Cyrillic alphabets include the Serbian, Macedonian, Bulgarian, and Russian alphabets. The Glagolitic alphabet is believed to have been created by Saints Cyril and Methodius, while the Cyrillic alphabet was invented by the Bulgarian scholar Clement of Ohrid, who was their disciple. They feature many letters that appear to have been borrowed from or influenced by the Greek alphabet and the Hebrew alphabet.

Asian alphabets[edit]

Beyond the logographic Chinese writing, many phonetic scripts are in existence in Asia. The Arabic alphabet, Hebrew alphabet, Syriac alphabet, and other abjads of the Middle East are developments of the Aramaic alphabet, but because these writing systems are largely consonant-based they are often not considered true alphabets.

Most alphabetic scripts of India and Eastern Asia are descended from the Brahmi script, which is often believed to be a descendant of Aramaic.

Zhuyin on a cell phone
In Korea, the Hangul alphabet was created by Sejong the Great[13] Hangul is a unique alphabet: it is a featural alphabet, where many of the letters are designed from a sound's place of articulation (P to look like the widened mouth, L to look like the tongue pulled in, etc.); its design was planned by the government of the day; and it places individual letters in syllable clusters with equal dimensions, in the same way as Chinese characters, to allow for mixed-script writing[citation needed] (one syllable always takes up one type-space no matter how many letters get stacked into building that one sound-block).

Zhuyin (sometimes called Bopomofo) is a semi-syllabary used to phonetically transcribe Mandarin Chinese in the Republic of China. After the later establishment of the People's Republic of China and its adoption of Hanyu Pinyin, the use of Zhuyin today is limited, but it's still widely used in Taiwan where the Republic of China still governs. Zhuyin developed out of a form of Chinese shorthand based on Chinese characters in the early 1900s and has elements of both an alphabet and a syllabary. Like an alphabet the phonemes of syllable initials are represented by individual symbols, but like a syllabary the phonemes of the syllable finals are not; rather, each possible final (excluding the medial glide) is represented by its own symbol. For example, luan is represented as ㄌㄨㄢ (l-u-an), where the last symbol ㄢ represents the entire final -an. While Zhuyin is not used as a mainstream writing system, it is still often used in ways similar to a romanization system—that is, for aiding in pronunciation and as an input method for Chinese characters on computers and cellphones.

European alphabets, especially Latin and Cyrillic, have been adapted for many languages of Asia. Arabic is also widely used, sometimes as an abjad (as with Urdu and Persian) and sometimes as a complete alphabet (as with Kurdish and Uyghur).

Types[edit]

Alphabets: Armenian , Cyrillic , Georgian , Greek , Latin , Latin (and Arabic) , Latin and Cyrillic
Abjads: Arabic , Hebrew
Abugidas: North Indic , South Indic , Ge'ez , Tāna , Canadian Syllabic and Latin
Logographic+syllabic: Pure logographic , Mixed logographic and syllabaries , Featural-alphabetic syllabary + limited logographic , Featural-alphabetic syllabary

History of the alphabet[show]

--------------------------------------------------------------------------------

The term "alphabet" is used by linguists and paleographers in both a wide and a narrow sense. In the wider sense, an alphabet is a script that is segmental at the phoneme level—that is, it has separate glyphs for individual sounds and not for larger units such as syllables or words. In the narrower sense, some scholars distinguish "true" alphabets from two other types of segmental script, abjads and abugidas. These three differ from each other in the way they treat vowels: abjads have letters for consonants and leave most vowels unexpressed; abugidas are also consonant-based, but indicate vowels with diacritics to or a systematic graphic modification of the consonants. In alphabets in the narrow sense, on the other hand, consonants and vowels are written as independent letters.[14] The earliest known alphabet in the wider sense is the Wadi el-Hol script, believed to be an abjad, which through its successor Phoenician is the ancestor of modern alphabets, including Arabic, Greek, Latin (via the Old Italic alphabet), Cyrillic (via the Greek alphabet) and Hebrew (via Aramaic).

Examples of present-day abjads are the Arabic and Hebrew scripts; true alphabets include Latin, Cyrillic, and Korean hangul; and abugidas are used to write Tigrinya, Amharic, Hindi, and Thai. The Canadian Aboriginal syllabics are also an abugida rather than a syllabary as their name would imply, since each glyph stands for a consonant which is modified by rotation to represent the following vowel. (In a true syllabary, each consonant-vowel combination would be represented by a separate glyph.)

All three types may be augmented with syllabic glyphs. Ugaritic, for example, is basically an abjad, but has syllabic letters for /ʔa, ʔi, ʔu/. (These are the only time vowels are indicated.) Cyrillic is basically a true alphabet, but has syllabic letters for /ja, je, ju/ (я, е, ю); Coptic has a letter for /ti/. Devanagari is typically an abugida augmented with dedicated letters for initial vowels, though some traditions use अ as a zero consonant as the graphic base for such vowels.

The boundaries between the three types of segmental scripts are not always clear-cut. For example, Sorani Kurdish is written in the Arabic script, which is normally an abjad. However, in Kurdish, writing the vowels is mandatory, and full letters are used, so the script is a true alphabet. Other languages may use a Semitic abjad with mandatory vowel diacritics, effectively making them abugidas. On the other hand, the Phagspa script of the Mongol Empire was based closely on the Tibetan abugida, but all vowel marks were written after the preceding consonant rather than as diacritic marks. Although short a was not written, as in the Indic abugidas, one could argue that the linear arrangement made this a true alphabet. Conversely, the vowel marks of the Tigrinya abugida and the Amharic abugida (ironically, the original source of the term "abugida") have been so completely assimilated into their consonants that the modifications are no longer systematic and have to be learned as a syllabary rather than as a segmental script. Even more extreme, the Pahlavi abjad eventually became logographic. (See below.)

Ge'ez Script of Ethiopia
Thus the primary classification of alphabets reflects how they treat vowels. For tonal languages, further classification can be based on their treatment of tone, though names do not yet exist to distinguish the various types. Some alphabets disregard tone entirely, especially when it does not carry a heavy functional load, as in Somali and many other languages of Africa and the Americas. Such scripts are to tone what abjads are to vowels. Most commonly, tones are indicated with diacritics, the way vowels are treated in abugidas. This is the case for Vietnamese (a true alphabet) and Thai (an abugida). In Thai, tone is determined primarily by the choice of consonant, with diacritics for disambiguation. In the Pollard script, an abugida, vowels are indicated by diacritics, but the placement of the diacritic relative to the consonant is modified to indicate the tone. More rarely, a script may have separate letters for tones, as is the case for Hmong and Zhuang. For most of these scripts, regardless of whether letters or diacritics are used, the most common tone is not marked, just as the most common vowel is not marked in Indic abugidas; in Zhuyin not only is one of the tones unmarked, but there is a diacritic to indicate lack of tone, like the virama of Indic.

The number of letters in an alphabet can be quite small. The Book Pahlavi script, an abjad, had only twelve letters at one point, and may have had even fewer later on. Today the Rotokas alphabet has only twelve letters. (The Hawaiian alphabet is sometimes claimed to be as small, but it actually consists of 18 letters, including the ʻokina and five long vowels.) While Rotokas has a small alphabet because it has few phonemes to represent (just eleven), Book Pahlavi was small because many letters had been conflated—that is, the graphic distinctions had been lost over time, and diacritics were not developed to compensate for this as they were in Arabic, another script that lost many of its distinct letter shapes. For example, a comma-shaped letter represented g, d, y, k, or j. However, such apparent simplifications can perversely make a script more complicated. In later Pahlavi papyri, up to half of the remaining graphic distinctions of these twelve letters were lost, and the script could no longer be read as a sequence of letters at all, but instead each word had to be learned as a whole—that is, they had become logograms as in Egyptian Demotic. The alphabet in the Polish language contains 32 letters.

The largest segmental script is probably an abugida, Devanagari. When written in Devanagari, Vedic Sanskrit has an alphabet of 53 letters, including the visarga mark for final aspiration and special letters for kš and jñ, though one of the letters is theoretical and not actually used. The Hindi alphabet must represent both Sanskrit and modern vocabulary, and so has been expanded to 58 with the khutma letters (letters with a dot added) to represent sounds from Persian and English.

The largest known abjad is Sindhi, with 51 letters. The largest alphabets in the narrow sense include Kabardian and Abkhaz (for Cyrillic), with 58 and 56 letters, respectively, and Slovak (for the Latin script), with 46. However, these scripts either count di- and tri-graphs as separate letters, as Spanish did with ch and ll until recently, or uses diacritics like Slovak č. The largest true alphabet where each letter is graphically independent is probably Georgian, with 41 letters.

Syllabaries typically contain 50 to 400 glyphs, and the glyphs of logographic systems typically number from the many hundreds into the thousands. Thus a simple count of the number of distinct symbols is an important clue to the nature of an unknown script.

Alphabetical order[edit]

Main article: Alphabetical order

Alphabets often come to be associated with a standard ordering of their letters, which can then be used for purposes of collation – namely for the listing of words and other items in what is called alphabetical order.

The basic ordering of the Latin alphabet (ABCDEFGHIJKLMNOPQRSTUVWXYZ), which is derived from the Northwest Semitic "Abgad" order,[15] is well established, although languages using this alphabet have different conventions for their treatment of modified letters (such as the French é, à, and ô) and of certain combinations of letters (multigraphs). In French, these are not considered to be additional letters for the purposes of collation. However, in Icelandic, the accented letters such as á, í, and ö are considered to be distinct letters of the alphabet. In Spanish, ñ is considered a separate letter, but accented vowels such as á and é are not. The ll and ch were also considered single letters, but in 1994 the Real Academia Española changed collating order so that ll is between lk and lm in the dictionary and ch is between cg and ci, and in 2010 the tenth congress of the Association of Spanish Language Academies changed it so they were no longer letters at all[16][17]

In German, words starting with sch- (constituting the German phoneme /ʃ/) would be intercalated between words with initial sca- and sci- (all incidentally loanwords) instead of this graphic cluster appearing after the letter s, as though it were a single letter—a lexicographical policy which would be de rigueur in a dictionary of Albanian, i.e. dh-, ë-, gj-, ll-, rr-, th-, xh- and zh- (all representing phonemes and considered separate single letters) would follow the letters d, e, g, l, n, r, t, x and z respectively. Nor is, in a dictionary of English, the lexical section with initial th- reserved a place after the letter t, but is inserted between te- and ti-. German words with umlaut would further be alphabetized as if there were no umlaut at all—contrary to Turkish which allegedly adopted the German graphemes ö and ü, and where a word like tüfek, would come after tuz, in the dictionary. An exception is the German phonebook where umlauts are sorted like ä = ae since names as Jäger appear also with the spelling Jaeger, and there's no telling them apart in the spoken language.

The Danish and Norwegian alphabets end with æ—ø—å, whereas the Icelandic, Swedish, Finnish and Estonian ones conventionally put å—ä—ö at the end.

It is unknown whether the earliest alphabets had a defined sequence. Some alphabets today, such as the Hanuno'o script, are learned one letter at a time, in no particular order, and are not used for collation where a definite order is required. However, a dozen Ugaritic tablets from the fourteenth century BC preserve the alphabet in two sequences. One, the ABCDE order later used in Phoenician, has continued with minor changes in Hebrew, Greek, Armenian, Gothic, Cyrillic, and Latin; the other, HMĦLQ, was used in southern Arabia and is preserved today in Ethiopic.[18] Both orders have therefore been stable for at least 3000 years.

The historical order was abandoned in Runic and Arabic, although Arabic retains the traditional abjadi order for numbering.

The Brahmic family of alphabets used in India use a unique order based on phonology: The letters are arranged according to how and where they are produced in the mouth. This organization is used in Southeast Asia, Tibet, Korean hangul, and even Japanese kana, which is not an alphabet.

Names of letters[edit]

The Phoenician letter names, in which each letter was associated with a word that begins with that sound, continue to be used to varying degrees in Samaritan, Aramaic, Syriac, Hebrew, Greek and Arabic. The names were abandoned in Latin, which instead referred to the letters by adding a vowel (usually e) before or after the consonant (the exception is zeta, which was retained from Greek). In Cyrillic originally the letters were given names based on Slavic words; this was later abandoned as well in favor of a system similar to that used in Latin.

Orthography and pronunciation[edit]

Main article: Phonemic orthography

When an alphabet is adopted or developed for use in representing a given language, an orthography generally comes into being, providing rules for the spelling of words in that language. In accordance with the principle on which alphabets are based, these rules will generally map letters of the alphabet to the phonemes (significant sounds) of the spoken language. In a perfectly phonemic orthography there would be a consistent one-to-one correspondence between the letters and the phonemes, so that a writer could predict the spelling of a word given its pronunciation, and a speaker could predict the pronunciation of a word given its spelling. However this ideal is not normally achieved in practice; some languages (such as Spanish and Finnish) come close to it, while others (such as English) deviate from it to a much larger degree.

The pronunciation of a language often evolves independently of its writing system, and writing systems have been borrowed for languages they were not designed for, so the degree to which letters of an alphabet correspond to phonemes of a language varies greatly from one language to another and even within a single language.

Languages may fail to achieve a one-to-one correspondence between letters and sounds in any of several ways:
A language may represent a given phoneme with a combination of letters rather than just a single letter. Two-letter combinations are called digraphs and three-letter groups are called trigraphs. German uses the tesseragraphs (four letters) "tsch" for the phoneme [tʃ] and "dsch" for [dʒ], although the latter is rare. Kabardian also uses a tesseragraph for one of its phonemes, namely "кхъу". Two letters representing one sound is widely used in Hungarian as well (where, for instance, cs stands for [č], sz for [s], zs for [ž], dzs for [ǰ], etc.).
A language may represent the same phoneme with two different letters or combinations of letters. An example is modern Greek which may write the phoneme [i] in six different ways: ⟨ι⟩, ⟨η⟩, ⟨υ⟩, ⟨ει⟩, ⟨οι⟩, and ⟨υι⟩ (although the last is rare).
A language may spell some words with unpronounced letters that exist for historical or other reasons. For example, the spelling of the Thai word for "beer" [เบียร์] retains a letter for the final consonant "r" present in the English word it was borrowed from, but silences it.
Pronunciation of individual words may change according to the presence of surrounding words in a sentence (sandhi).
Different dialects of a language may use different phonemes for the same word.
A language may use different sets of symbols or different rules for distinct sets of vocabulary items, such as the Japanese hiragana and katakana syllabaries, or the various rules in English for spelling words from Latin and Greek, or the original Germanic vocabulary.

National languages generally elect to address the problem of dialects by simply associating the alphabet with the national standard. However, with an international language with wide variations in its dialects, such as English, it would be impossible to represent the language in all its variations with a single phonetic alphabet.

Some national languages like Finnish, Turkish, Serbo-Croatian (Serbian, Croatian and Bosnian) and Bulgarian have a very regular spelling system with a nearly one-to-one correspondence between letters and phonemes. Strictly speaking, these national languages lack a word corresponding to the verb "to spell" (meaning to split a word into its letters), the closest match being a verb meaning to split a word into its syllables. Similarly, the Italian verb corresponding to 'spell (out)', compitare, is unknown to many Italians because the act of spelling itself is rarely needed: Italian spelling is highly phonemic. In standard Spanish, it is possible to tell the pronunciation of a word from its spelling, but not vice versa; this is because certain phonemes can be represented in more than one way, but a given letter is consistently pronounced. French, with its silent letters and its heavy use of nasal vowels and elision, may seem to lack much correspondence between spelling and pronunciation, but its rules on pronunciation, though complex, are actually consistent and predictable with a fair degree of accuracy.

At the other extreme are languages such as English, where the spelling of many words simply has to be memorized as they do not correspond to sounds in a consistent way. For English, this is partly because the Great Vowel Shift occurred after the orthography was established, and because English has acquired a large number of loanwords at different times, retaining their original spelling at varying levels. Even English has general, albeit complex, rules that predict pronunciation from spelling, and these rules are successful most of the time; rules to predict spelling from the pronunciation have a higher failure rate.

Sometimes, countries have the written language undergo a spelling reform to realign the writing with the contemporary spoken language. These can range from simple spelling changes and word forms to switching the entire writing system itself, as when Turkey switched from the Arabic alphabet to a Turkish alphabet of Latin origin.

The sounds of speech of all languages of the world can be written by a rather-small universal phonetic-alphabet. A standard for this is the International Phonetic Alphabet.

See also[edit]

A Is For Aardvark
Abecedarium
Acrophony
Akshara
Alphabet Effect
Alphabet song
Alphabetical order
Alphabetize
Butterfly Alphabet
Character encoding
Constructed script
Cyrillic
English alphabet
Hangul
ICAO spelling alphabet
Lipogram
List of alphabets
Pangram
Thai script
Transliteration
Unicode

References[edit]

1.^ Coulmas, Florian (1996). The Blackwell Encyclopedia of Writing Systems. Oxford: Blackwell Publishing. ISBN 0-631-21481-X.
2.^ Millard 1986, p. 396
3.^ Haarmann 2004, p. 96
4.^ Encyclopædia Britannica Online – Merriam-Webster's Online Dictionary
5.^ "The Development of the Western Alphabet". h2g2. BBC. 2004-04-08. Retrieved 2008-08-04.
6.^ Daniels and Bright (1996), pp. 74–75
7.^ J. C. Darnell, F. W. Dobbs-Allsopp, Marilyn J. Lundberg, P. Kyle McCarter, and Bruce Zuckermanet, “Two early alphabetic inscriptions from the Wadi el-Hol: new evidence for the origin of the alphabet from the western desert of Egypt.” The Annual of the American Schools of Oriental Research, 59 (2005).
8.^ a b Coulmas (1989), p. 140–141.
9.^ Ugaritic Writing online
10.^ a b c Daniels and Bright (1996), pp 92-96
11.^ "Coulmas"(1989),p.142
12.^ "Coulmas" (1989) p.147.
13.^ "上親制諺文二十八字…是謂訓民正音(His majesty created 28 characters himself... It is Hunminjeongeum (original name for Hangul))", 《세종실록 (The Annals of the Choson Dynasty : Sejong)》 25년 12월.
14.^ For critics of the abjad-abugida-alphabet distinction, see Reinhard G. Lehmann: "27-30-22-26. How Many Letters Needs an Alphabet? The Case of Semitic", in: The idea of writing: Writing across borders / edited by Alex de Voogt and Joachim Friedrich Quack, Leiden: Brill 2012, p. 11-52, esp p. 22-27
15.^ Reinhard G. Lehmann: "27-30-22-26. How Many Letters Needs an Alphabet? The Case of Semitic", in: The idea of writing: Writing across borders / edited by Alex de Voogt and Joachim Friedrich Quack, Leiden: Brill 2012, p. 11-52
16.^ Real Academia Española. "Spanish Pronto!: Spanish Alphabet." Spanish Pronto! 22 April 2007. January 2009 Spanish Pronto: Spanish < > English Medical Translators.
17.^ "La “i griega” se llamará “ye”". Cuba Debate. 2010-11-05. Retrieved 12 December 2010. Cubadebate.cu
18.^ Millard, A.R. "The Infancy of the Alphabet", World Archaeology 17, No. 3, Early Writing Systems (February 1986): 390–398. page 395.

Bibliography[edit]
Coulmas, Florian (1989). The Writing Systems of the World. Blackwell Publishers Ltd. ISBN 0-631-18028-1.
Daniels, Peter T.; Bright, William (1996). The World's Writing Systems. Oxford University Press. ISBN 0-19-507993-0. Overview of modern and some ancient writing systems.
Driver, G. R. (1976). Semitic Writing (Schweich Lectures on Biblical Archaeology S.) 3Rev Ed. Oxford University Press. ISBN 0-19-725917-0.
Haarmann, Harald (2004). Geschichte der Schrift (2nd ed.). München: C. H. Beck. ISBN 3-406-47998-7
Hoffman, Joel M. (2004). In the Beginning: A Short History of the Hebrew Language. NYU Press. ISBN 0-8147-3654-8. Chapter 3 traces and summarizes the invention of alphabetic writing.
Logan, Robert K. (2004). The Alphabet Effect: A Media Ecology Understanding of the Making of Western Civilization. Hampton Press. ISBN 1-57273-523-6.
McLuhan, Marshall; Logan, Robert K. (1977). Alphabet, Mother of Invention. Etcetera. Vol. 34, pp. 373–383
Millard, A. R. (1986). "The Infancy of the Alphabet". World Archaeology 17 (3): 390–398. doi:10.1080/00438243.1986.9979978
Ouaknin, Marc-Alain; Bacon, Josephine (1999). Mysteries of the Alphabet: The Origins of Writing. Abbeville Press. ISBN 0-7892-0521-1.
Powell, Barry (1991). Homer and the Origin of the Greek Alphabet. Cambridge University Press. ISBN 0-521-58907-X.
Powell, Barry B. 2009. Writing: Theory and History of the Technology of Civilization, Oxford: Blackwell. ISBN 978-1-4051-6256-2
Sacks, David (2004). Letter Perfect: The Marvelous History of Our Alphabet from A to Z (PDF). Broadway Books. ISBN 0-7679-1173-3.
Saggs, H. W. F. (1991). Civilization Before Greece and Rome. Yale University Press. ISBN 0-300-05031-3. Chapter 4 traces the invention of writing

External links[edit]

Look up alphabet in Wiktionary, the free dictionary.
The Origins of abc
"Language, Writing and Alphabet: An Interview with Christophe Rico", Damqātum 3 (2007)
Alphabetic Writing Systems
Michael Everson's Alphabets of Europe
Evolution of alphabets, animation by Prof. Robert Fradkin at the University of Maryland
How the Alphabet Was Born from Hieroglyphs—Biblical Archaeology Review

 

 

English alphabet - Wikipedia, the free encyclopedia

en.wikipedia.org/wiki/English_alphabet‎

The modern English alphabet is a Latin alphabet consisting of 26 letters – the same letters that are found in the ISO basic Latin alphabet: ...

 

 

THE USBORNE BOOK OF

FACTS AND LISTS

Lynn Bressler (no date)

Page 82

10 most spoken languages
Chinese 700,000,000 English 400,000,000 Russian 265,000,000 Spanish 240,000,000 Hindustani 230,000,000 Arabic 146,000,000 Portuguese 145,000,000 Bengali 144,000,000 German 119,000,000 Japanese 116,000,000

The first alphabet
The Phoenicians, who once lived where Syria, Jordan and Lebanon are today, had an alphabet of 29 letters as early as 1,700 BC. It was adopted by the Greeks and the Romans. Through the Romans, who went on to conquer most of Europe, it became the alphabet of Western countries.

Sounds strange
One tribe of Mexican Indians hold entire conversations just by whistling. The different pitches provide meaning.

The Rosetta Stone
 The Rosetta Stone was found by Napoleon in the sands of Egypt. It dates to about 196 BC.
On it is an inscription in hieroglyphics and a translation in Greek. , Because scholars knew ancient Greek, they could work out what the Egyptian hieroglyphics meant. From this they learned the language of the ancient Egyptians.

Did You KnowMany Chinese cannot understand each other. They have different ways of speaking (called dialects) in different
parts of the country. But today in schools allover China, the children are being taught one dialect (Mandarin), so that one day all Chinese will understand each other.

Translating computers
Computers can be used to help people of different nationalities, who do not know each others' language, talk to each other. By giving a computer a message in one language it will translate it into another specified language.

Worldwide language
English is spoken either as a first or second language in at least 45 countries. This is more than any other language. It is the language of international business and scientific conferences and is used by airtraffic controllers worldwide. In all, about one third of the world speaks it.

Page 83

Earliest writing Chinese writing has been found on pottery, and even on a tortoise shell, going back 6,000 years. Pictures made the basis for their writing, each picture showing an object or idea. Probably the earliest form of writing came from the Middle East, where Iraq and Iran are now. This region was then ruled by the Sumerians.

The most words

English has more words in it than any other language. There are about1 million in all, a third of which are technical terms. Most
people only use about 1 per cent of the words available, that is, about 10,000. William Shakespeare is reputed to have made most use of the English vocabulary.

A scientific word describing a process in the human cell is 207,000 letters long. This makes this single word equal in length to a short novel or about 80 typed sheets of A4 paper.

Many tongues
A Frenchman, named Georges Henri Schmidt, is fluent (meaning he reads and writes well) in 31 different languages.

International language
Esperanto was invented in the 1880s by a Pole, Dr Zamenhof. It was hoped that it would become the international language of Europe. It took words from many European countries and has a very easy grammar that can be learned in an hour or two.
The same language

The languages of India and Europe may originally come from just one source. Many words in different languages sound similar. For example, the word for King in Latin is Rex, in Indian, Raj, in Italian Re, in French Roi and in Spanish Rey. The original language has been named Indo-European. Basque, spoken in the French and Spanish Pyrenees, is an exception. It seems to have a different source which is still unknown.

Number of alphabets
There are 65 alphabets in use in the world today. Here are some of them: Roman
ABCDEFGHUKLMNOPQRS Greek  Russian (Cyrillic) Hebrew  Chinese (examples omitted)

 

 

 

26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
8
9
-
-
-
-
5
6
-
-
-
1
-
-
-
-
6
-
8
+
=
43
4+3
=
7
-
7
-
7
-
-
-
-
-
-
-
-
8
9
-
-
-
-
14
15
-
-
-
19
-
-
-
-
24
-
26
+
=
115
1+1+5
=
7
-
7
-
7
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
-
-
1
2
3
4
-
-
7
8
9
-
2
3
4
5
-
7
-
+
=
83
8+3
=
11
1+1
2
-
2
-
1
2
3
4
5
6
7
-
-
10
11
12
13
-
-
16
17
18
-
20
21
22
23
-
25
-
+
=
236
2+3+6
=
11
1+1
2
-
2
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
+
=
351
3+5+1
=
9
-
9
-
9
-
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
+
=
126
1+2+6
=
9
-
9
-
9
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
-
1
-
-
-
-
-
-
-
+
=
1
occurs
x
3
=
3
-
3
-
-
2
-
-
-
-
-
-
-
-
2
-
-
-
-
-
-
-
-
2
-
-
-
-
-
-
+
=
2
occurs
x
3
=
6
-
6
-
-
-
3
-
-
-
-
-
-
-
-
3
-
-
-
-
-
-
-
-
3
-
-
-
-
-
+
=
3
occurs
x
3
=
9
-
9
-
-
-
-
4
-
-
-
-
-
-
-
-
4
-
-
-
-
-
-
-
-
4
-
-
-
-
+
=
4
occurs
x
3
=
12
1+2
3
-
-
-
-
-
5
-
-
-
-
-
-
-
-
5
-
-
-
-
-
-
-
-
5
-
-
-
+
=
5
occurs
x
3
=
15
1+5
6
-
-
-
-
-
-
6
-
-
-
-
-
-
-
-
6
-
-
-
-
-
-
-
-
6
-
-
+
=
6
occurs
x
3
=
18
1+8
9
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
-
7
-
+
=
7
occurs
x
3
=
21
2+1
3
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
-
-
8
+
=
8
occurs
x
3
=
24
2+4
6
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
+
=
9
occurs
x
2
=
18
1+8
9
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
45
-
-
26
-
126
-
54
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
4+5
-
-
2+6
-
1+2+6
-
5+4
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
9
-
-
8
-
9
-
9
-
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
-
-
-
-
-
-
-
-
-
-
26
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
9
-
-
8
-
9
-
9

 

 

 

English alphabet

From Wikipedia, the free encyclopedia

Jump to: navigation, search

"The Alphabet" redirects here. For the short film by David Lynch, see The Alphabet (film).

The modern English alphabet is a Latin alphabet consisting of 26 letters – the same letters that are found in the ISO basic Latin alphabet:

Majuscule forms (also called uppercase or capital letters)
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Minuscule forms (also called lowercase or small letters)
a b c d e f g h i j k l m n o p q r s t u v w x y z

The exact shape of printed letters varies depending on the typeface. The shape of handwritten letters can differ significantly from the standard printed form (and between individuals), especially when written in cursive style. See the individual letter articles for information about letter shapes and origins (follow the links on any of the uppercase letters above).

Written English uses a number of digraphs, such as ch, sh, th, wh, qu, etc., but they are not considered separate letters of the alphabet. Some traditions also use two ligatures, æ and œ,[1] or consider the ampersand (&) part of the alphabet.

English alphabet

Contents
[hide] 1 History 1.1 Old English
1.2 Modern English

2 Diacritics
3 Ampersand
4 Apostrophe
5 Letter names 5.1 Etymology

6 Phonology
7 Letter frequencies
8 See also
9 Footnotes

History[edit]

See also: History of the Latin alphabet and English orthography

Old English[edit]

Main article: Old English Latin alphabet

The English language was first written in the Anglo-Saxon futhorc runic alphabet, in use from the 5th century. This alphabet was brought to what is now England, along with the proto-form of the language itself, by Anglo-Saxon settlers. Very few examples of this form of written Old English have survived, these being mostly short inscriptions or fragments.

The Latin script, introduced by Christian missionaries, began to replace the Anglo-Saxon futhorc from about the 7th century, although the two continued in parallel for some time. Futhorc influenced the emerging English alphabet by providing it with the letters thorn (Þ þ) and wynn (Ƿ ƿ). The letter eth (Ð ð) was later devised as a modification of dee (D d), and finally yogh (Ȝ ȝ) was created by Norman scribes from the insular g in Old English and Irish, and used alongside their Carolingian g.

The a-e ligature ash (Æ æ) was adopted as a letter its own right, named after a futhorc rune æsc. In very early Old English the o-e ligature ethel (Œ œ) also appeared as a distinct letter, likewise named after a rune, œðel. Additionally, the v-v or u-u ligature double-u (W w) was in use.

In the year 1011, a writer named Byrhtferð ordered the Old English alphabet for numerological purposes.[2] He listed the 24 letters of the Latin alphabet (including ampersand) first, then 5 additional English letters, starting with the Tironian note ond (⁊) an insular symbol for and:
A B C D E F G H I K L M N O P Q R S T V X Y Z & ⁊ Ƿ Þ Ð Æ
Modern English[edit]

In the orthography of Modern English, thorn (þ), eth (ð), wynn (ƿ), yogh (ȝ), ash (æ), and ethel (œ) are obsolete. Latin borrowings reintroduced homographs of ash and ethel into Middle English and Early Modern English, though they are not considered to be the same letters[citation needed] but rather ligatures, and in any case are somewhat old-fashioned. Thorn and eth were both replaced by th,[citation needed] though thorn continued in existence for some time, its lowercase form gradually becoming graphically indistinguishable from the minuscule y in most handwriting. Y for th can still be seen in pseudo-archaisms such as "Ye Olde Booke Shoppe". The letters þ and ð are still used in present-day Icelandic and Faroese. Wynn disappeared from English around the fourteenth century when it was supplanted by uu, which ultimately developed into the modern w. Yogh disappeared around the fifteenth century and was typically replaced by gh.

The letters u and j, as distinct from v and i, were introduced in the 16th century, and w assumed the status of an independent letter, so that the English alphabet is now considered to consist of the following 26 letters:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
The variant lowercase form long s (ſ) lasted into early modern English, and was used in non-final position up to the early 19th century.

The ligatures æ and œ are still used in formal writing for certain words of Greek or Latin origin, such as encyclopædia and cœlom. Lack of awareness and technological limitations (such as their absence from the standard qwerty keyboard) have made it common to see these rendered as "ae" and "oe", respectively, in modern, non-academic usage. These ligatures are not used in American English, where a lone e has mostly supplanted both (for example, encyclopedia for encyclopædia, and fetus for fœtus).

Diacritics[edit]

Main article: English terms with diacritical marks

Question book-new.svg
This section does not cite any references or sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (June 2011)

Diacritic marks mainly appear in loanwords such as naïve and façade. As such words become naturalised In English, there is a tendency to drop the diacritics, as has happened with old borrowings such as hôtel, from French. Informal English writing tends to omit diacritics because of their absence from the computer keyboard, while professional copywriters and typesetters tend to include them. Words that are still perceived as foreign tend to retain them; for example, the only spelling of soupçon found in English dictionaries (the OED and others) uses the diacritic. Diacritics are also more likely to be retained where there would otherwise be confusion with another word (for example, résumé rather than resume), and, rarely, even added (as in maté, from Spanish yerba mate, but following the pattern of café, from French).

Occasionally, especially in older writing, diacritics are used to indicate the syllables of a word: cursed (verb) is pronounced with one syllable, while cursèd (adjective) is pronounced with two. È is used widely in poetry, e.g. in Shakespeare's sonnets. Similarly, while in chicken coop the letters -oo- represent a single vowel sound (a digraph), in zoölogist and coöperation, they represent two. An acute, grave or diaeresis may also be placed over an 'e' at the end of a word to indicate that it is not silent, as in saké. However, in practice these devices are often not used even where they would serve to alleviate some degree of confusion.

Ampersand[edit]

The & has sometimes appeared at the end of the English alphabet, as in Byrhtferð's list of letters in 1011.[2] Historically, the figure is a ligature for the letters Et. In English it is used to represent the word and and occasionally the Latin word et, as in the abbreviation &c (et cetera).

Apostrophe[edit]

Question book-new.svg
This section does not cite any references or sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (June 2011)

The apostrophe, while not considered part of the English alphabet, is used to abbreviate English words. A few pairs of words, such as its (belonging to it) and it's (it is or it has), were (plural of was) and we're (we are), and shed (to get rid of) and she'd (she would or she had) are distinguished in writing only by the presence or absence of an apostrophe. The apostrophe also distinguishes the possessive endings -'s and -s' from the common plural ending -s, a practice introduced in the 18th century; before, all three endings were written -s, which could lead to confusion (as in, the Apostles words).

Letter names[edit]

The names of the letters are rarely spelled out, except when used in derivations or compound words (for example tee-shirt, deejay, emcee, okay, aitchless, wye-level, etc.), derived forms (for example exed out, effing, to eff and blind, etc.), and in the names of objects named after letters (for example em (space) in printing and wye (junction) in railroading). The forms listed below are from the Oxford English Dictionary. Vowels stand for themselves, and consonants usually have the form consonant + ee or e + consonant (e.g. bee and ef). The exceptions are the letters aitch, jay, kay, cue, ar, ess (but es- in compounds ), wye, and zed. Plurals of consonants end in -s (bees, efs, ems) or, in the cases of aitch, ess, and ex, in -es (aitches, esses, exes). Plurals of vowels end in -es (aes, ees, ies, oes, ues); these are rare. Of course, all letters may stand for themselves, generally in capitalized form (okay or OK, emcee or MC), and plurals may be based on these (aes or A's, cees or C's, etc.)

Letter

Letter name

Pronunciation

A a /eɪ/[3]
B bee /biː/
C cee /siː/
D dee /diː/
E e /iː/
F ef (eff as a verb) /ɛf/
G gee /dʒiː/
H aitch /eɪtʃ/
haitch[4] /heɪtʃ/
I i /aɪ/
J jay /dʒeɪ/
jy[5] /dʒaɪ/
K kay /keɪ/
L el or ell /ɛl/
M em /ɛm/
N en /ɛn/
O o /oʊ/
P pee /piː/
Q cue /kjuː/
R ar /ɑr/[6]
S ess (es-)[7] /ɛs/
T tee /tiː/
U u /juː/
V vee /viː/
W double-u /ˈdʌbəl.juː/[8]
X ex /ɛks/
Y wy or wye /waɪ/
Z zed[9] /zɛd/
zee[10] /ziː/
izzard[11] /ˈɪzərd/

Some groups of letters, such as pee and bee, or em and en, are easily confused in speech, especially when heard over the telephone or a radio communications link. Spelling alphabets such as the ICAO spelling alphabet, used by aircraft pilots, police and others, are designed to eliminate this potential confusion by giving each letter a name that sounds quite different from any other.

Etymology[edit]

The names of the letters are for the most part direct descendents, via French, of the Latin (and Etruscan) names. (See Latin alphabet: Origins.)

Letter

Latin

Old French

Middle English

Modern English

A á /aː/ /aː/ /aː/ /eɪ/
B bé /beː/ /beː/ /beː/ /biː/
C cé /keː/ /tʃeː/ → /tseː/ → /seː/ /seː/ /siː/
D dé /deː/ /deː/ /deː/ /diː/
E é /eː/ /eː/ /eː/ /iː/
F ef /ɛf/ /ɛf/ /ɛf/ /ɛf/
G gé /ɡeː/ /dʒeː/ /dʒeː/ /dʒiː/
H há /haː/ → /aha/ → /akːa/ /aːtʃ/ /aːtʃ/ /eɪtʃ/
I í /iː/ /iː/ /iː/ /aɪ/
J – – – /dʒeɪ/
K ká /kaː/ /kaː/ /kaː/ /keɪ/
L el /ɛl/ /ɛl/ /ɛl/ /ɛl/
M em /ɛm/ /ɛm/ /ɛm/ /ɛm/
N en /ɛn/ /ɛn/ /ɛn/ /ɛn/
O ó /oː/ /oː/ /oː/ /oʊ/
P pé /peː/ /peː/ /peː/ /piː/
Q qú /kuː/ /kyː/ /kiw/ /kjuː/
R er /ɛr/ /ɛr/ / ɛr/ → /ar/ /ɑr/
S es /ɛs/ /ɛs/ /ɛs/ /ɛs/
T té /teː/ /teː/ /teː/ /tiː/
U ú /uː/ /yː/ /iw/ /juː/
V – – – /viː/
W – – – /ˈdʌbəl.juː/
X ex /ɛks, iks/ /iks/ /ɛks/ /ɛks/
Y hý /hyː, iː/
í graeca /ˈɡraɪka/ ui, gui ?
i grec /iː ɡrɛːk/ /wiː/ ? /waɪ/
Z zéta /zeːta/ zed /zɛːd/
et zed /et zeːd/ → /e zed/ /zɛd/
/ɛˈzɛd/ /zɛd, ziː/
/ˈɪzəd/

The regular phonological developments (in rough chronological order) are:
palatalization before front vowels of Latin /k/ successively to /tʃ/, /ts/, and finally to Middle French /s/. Affects C.
palatalization before front vowels of Latin /ɡ/ to Proto-Romance and Middle French /dʒ/. Affects G.
fronting of Latin /uː/ to Middle French /yː/, becoming Middle English /iw/ and then Modern English /juː/. Affects Q, U.
the inconsistent lowering of Middle English /ɛr/ to /ar/. Affects R.
the Great Vowel Shift, shifting all Middle English long vowels. Affects A, B, C, D, E, G, H, I, K, O, P, T, and presumably Y.

The novel forms are aitch, a regular development of Medieval Latin acca; jay, a new letter presumably vocalized like neighboring kay to avoid confusion with established gee (the other name, jy, was taken from French); vee, a new letter named by analogy with the majority; double-u, a new letter, self-explanatory (the name of Latin V was ū); wye, of obscure origin but with an antecedent in Old French wi; zee, an American leveling of zed by analogy with the majority; and izzard, from the Romance phrase i zed or i zeto "and Z" said when reciting the alphabet.

Phonology[edit]

Main article: English phonology

The letters A, E, I, O, and U are considered vowel letters, since (except when silent) they represent vowels; the remaining letters are considered consonant letters, since when not silent they generally represent consonants. However, Y commonly represents vowels as well as a consonant (e.g., "myth"), as very rarely does W (e.g., "cwm"). Conversely, U sometimes represents a consonant (e.g., "quiz").

Letter frequencies[edit]

Main article: Letter frequency

The letter most frequently used in English is E. The least frequently used letter is Z.

The list below shows the frequency of letter use in English.[12]

Letter

Frequency

A 8.17%
B 1.49%
C 2.78%
D 4.25%
E 12.70%
F 2.23%
G 2.02%
H 6.09%
I 6.97%
J 0.15%
K 0.77%
L 4.03%
M 2.41%
N 6.75%
O 7.51%
P 1.93%
Q 0.10%
R 5.99%
S 6.33%
T 9.06%
U 2.76%
V 0.98%
W 2.36%
X 0.15%
Y 1.97%
Z 0.07%

See also[edit]
English orthography
English spelling reform
American manual alphabet
Two-handed manual alphabets
English braille
American braille
New York Point

Footnotes[edit]

1.^ See also the section on Ligatures
2.^ a b Michael Everson, Evertype, Baldur Sigurðsson, Íslensk Málstöð, On the Status of the Latin Letter Þorn and of its Sorting Order
3.^ Sometimes /æ/ in Hiberno-English
4.^ sometimes in Australian and Irish English, and usually in Indian English (although often considered incorrect)
5.^ in Scottish English
6.^ /ɔr/ (/ɔər/?) in Hiberno-English[citation needed]
7.^ in compounds such as es-hook
8.^ Especially in American English, the /l/ is not often pronounced in informal speech. (Merriam Webster's Collegiate Dictionary, 10th ed). Common colloquial pronunciations are /ˈdʌbəjuː/, /ˈdʌbəjə/, and /ˈdʌbjə/, as in the nickname "Dubya", especially in terms like www.
9.^ in British and Commonwealth English
10.^ in American English
11.^ in Scottish English
12.^ Beker, Henry; Piper, Fred (1982). Cipher Systems: The Protection of Communications. Wiley-Interscience. p. 397. Table also available from Lewand, Robert (2000). Cryptological Mathematics. The Mathematical Association of America. p. 36. ISBN 978-0883857199. and [1]


Description of the English language

Grammar·
Phonology·
Stress and reduced vowels·
Orthography·
Alphabet·
Dialects·
Language history·
Phonological history

Categories: English spelling
Latin alphabets

Languages

العربية
Български
Česky
Deutsch
Eesti
Español
فارسی
Français
Gaelg
한국어
हिन्दी
Magyar
Македонски
Polski
Português
Română
Русский
தமிழ்
Тоҷикӣ
Türkçe
Українська
中文
Edit links

This page was last modified on 5 June 2013 at 05:21.

 

1234 5 6789

Letter frequency - Wikipedia, the free encyclopedia

"The most common letter in the English alphabet is E."

 

Daily Mail, Wednesday, December 10, 2014

ANSWERS TO CORRESPONDENTS

Compiled by Charles Legge

QUESTION A Iipogram Is a constrained form of writing where a specific letter (often a vowel) is avoided altogether. Have any novels been written this way?

THE lipogram (Greek for 'leaving out a letter') is an ancient literary form, dating back to the 6th-century BC writer Lasus of Hermione, who wrote two composition for the voice in which he suppressed the sigma, one of the most common letters in Greek.
The first person to tackle it in novel form was U.S. author Ernest Vincent Wright, Gadsby, published in 1939, has 50,000 words and is completely without the letter E. The hero of the novel is a man named John Gadsby. The author went so far as to make the E on his typewriter inoperable, to avoid an E slipping into the text inadvertently.
Naturally he had to avoid the word pronouns such as 'he', 'she', 'her', 'them' `they', and past tenses that end in '-ed'. The numbers from seven to 30 had to be omitted as, to keep the text 'pure' the author would not substitute the numerical values — quite an achievement. It took about nine years to complete then some time to find a publisher.
A poetic lipogram, probably unintentional, is the six-line nursery rhyme Old Mother Hubbard which, surprisingly, does not contain the letter i.
Going further, there is one three-stanza poem, called Fate Of Nassan, in which each four-line stanza contains every letter of the alphabet except 'e'. The poem is anonymous but was composed before 1870.
C. D. Allan, Alsager, Stoke-on-Trent, Staffs.

PERHAPS the most-famous example is the Polish-Jewish-French writer Georges Perec, who died in 1982.
His 1969 novel, La Disparition, translated. into English (1994) by Gilbert Adair as A Void, was written without a single letter `e'. Ironic, really, since his own name contains no fewer than four example of that letter.
Frederick Robinson, Bexhill-on-Sea, East Sussex

 



Old Mother Hubbard - Wikipedia, the free encyclopedia
en.wikipedia.org/wiki/Old_Mother_Hubbard

Old Mother Hubbard Went to the cupboard, To give the poor dog a bone; When she came there, The cupboard was bare, And so the poor dog had none.

 

 

Letter frequency - Wikipedia, the free encyclopedia

"The most common letter in the English alphabet is E."

LOOK AT THE 5FIVES LOOK AT THE 5FIVES LOOK AT THE 5FIVES THE 5FIVES THE 5FIVES

LOOK AT THE 5 LOOK AT THE 5 LOOK AT THE 5 THE 5 THE 5

 



Daily Mail

Thursday, June 11 2009

Page 37

Web 2.0 - the one millionth English word

ALMOST 1,500 years after it was first recorded, the English language has its one millionth word.

At 10.22am yesterday Web 2.0 - describing the next generation of internet services entered the dictionary.

To be accepted a word must be used at least 25,000 times across national boundaries and outside specialisms.

U.S-based Global Language Monitor surveys print publications, online news sites, blogs and social media for useage.

Jai Ho!, a Hindi phrase signifying the joy of victory became the 999,999th word thanks to the Oscar-Winning film Slumdog millionaire.

At 1,000,001 is Financial Tsunami - a sudden financial restructuring.

"JAI HO! A HINDI PHRASE SIGNIFYING THE JOY OF VICTORY BECAME THE 999,999TH WORD..."

 

 

 

A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
-
-
-
-
-
-
-
-
-
1+0
1+1
1+2
1+3
1+4
1+5
1+6
1+7
1+8
1+9
2+0
2+1
2+2
2+3
2+4
2+5
2+6
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z

 

 

 

LANGUAGE LAND ENGAGE LAND LANGUAGE

LETTERS AND NUMBERS AND LETTERS

 

 

THE JESUS MYSTERIES

Timothy Freke & Peter Gandy

1

999

Page 177

The gospels are actually anonymous works, in which everything, without exception, is written in capital letters, with no headings, chapter or verse divisions, and practically no punctuation or spaces between words.61 They were not even written in the Aramic of the Jews but in Greek.62

 

THE GOSPELS ARE ACTUALLY ANONYMOUS WORKS,

IN WHICH EVERYTHING WITHOUT EXCEPTION, IS WRITTEN IN CAPITAL LETTERS,

WITH NO PUNCTUATION OR SPACES BETWEEN WORDS.

 

 

T
=
2
-
7
THE
33
15
6
-
-
-
-
-
-
-
-
-
G
=
7
-
-
GOSPELS
-
-
-
-
-
-
-
1
G
7
7
7
-
-
-
-
2
O+S
34
16
7
-
-
-
-
1
P
16
7
7
-
-
-
-
3
E+L+S
36
18
9
G
=
7
-
7
GOSPELS
93
48
30
-
-
-
-
-
-
9+3
4+8
3+0
G
=
7
-
7
GOSPELS
12
12
3
-
-
-
-
-
-
1+2
1+2
-
G
=
7
-
7
GOSPELS
3
3
3

 

 

T
=
2
-
3
THE
33
15
6
G
=
7
-
7
GOSPELS
93
48
30
-
-
9
-
10
-
126
63
36
-
-
-
-
1+0
Q
1+2+6
6+3
3+6
-
-
9
Q
1
-
9
9
9

 

 

GODS PEOPLES GODS

GOD SPELLS GOSPELS SPELLS GOD

 

 

T
=
2
-
7
THE
33
15
6
-
-
-
-
-
-
-
-
-
E
=
5
-
-
ESSENES
-
-
-
-
-
-
-
1
E
5
5
5
-
-
-
-
2
S+S
38
20
2
-
-
-
-
1
E
5
5
5
-
-
-
-
1
N
14
5
5
-
-
-
-
1
E
5
5
5
-
-
-
-
1
S
19
10
1
E
=
5
-
7
ESSENES
86
50
23
-
-
-
-
-
-
8+6
5+0
2+3
E
=
5
-
7
ESSENES
14
5
5
-
-
-
-
-
-
1+4
-
-
E
=
5
-
7
ESSENES
5
5
5

 

 

T
=
2
-
7
THE
33
15
6
-
-
-
-
-
-
-
-
-
E
=
5
-
-
ESSENES
-
-
-
-
-
-
-
1
E
5
5
5
-
-
-
-
6
SENSES
81
18
9
E
=
5
-
7
ESSENES
86
23
14
-
-
-
-
-
-
8+6
2+3
1+4
E
=
5
-
7
ESSENES
14
5
5
-
-
-
-
-
-
1+4
-
-
E
=
5
-
7
ESSENES
5
5
5

 

 

Essenes - Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Essenes‎

The Essenes (in Modern but not in Ancient Hebrew: אִסִּיִים, Isiyim; Greek: Εσσήνοι, Εσσαίοι, or Οσσαίοι, Essḗnoi, Essaíoi, Ossaíoi) were a sect of Second ...

Essenes

From Wikipedia, the free encyclopedia

Essene" redirects here. For the bread, see sprouted bread.

Part of a series on Jews and Judaism

Star of David

­Etymology·
­Who is a Jew?
­Jewish peoplehood
­Jewish identity

Religion[show]

The Essenes (in Modern but not in Ancient Hebrew: אִסִּיִים, Isiyim; Greek: Εσσήνοι, Εσσαίοι, or Οσσαίοι, Essḗnoi, Essaíoi, Ossaíoi) were a sect of Second Temple Judaism that flourished from the 2nd century BCE to the 1st century CE which some scholars claim seceded from the Zadokite priests.[1] Being much fewer in number than the Pharisees and the Sadducees (the other two major sects at the time), the Essenes lived in various cities but congregated in communal life dedicated to asceticism, voluntary poverty, daily immersion, and abstinence from worldly pleasures, including (for some groups) celibacy. Many separate but related religious groups of that era shared similar mystic, eschatological, messianic, and ascetic beliefs. These groups are collectively referred to by various scholars as the "Essenes." Josephus records that Essenes existed in large numbers, and thousands lived throughout Roman Judæa.

The Essenes have gained fame in modern times as a result of the discovery of an extensive group of religious documents known as the Dead Sea Scrolls, which are commonly believed to be Essenes' library—although there is no proof that the Essenes wrote them. These documents include preserved multiple copies of the Hebrew Bible untouched from as early as 300 BCE until their discovery in 1946. Some scholars, however, dispute the notion that the Essenes wrote the Dead Sea Scrolls.[2] Rachel Elior questions even the existence of the Essenes.[3][4][5]

The first reference is by the Roman writer Pliny the Elder (died c. 79 CE) in his Natural History.[6] Pliny relates in a few lines that the Essenes do not marry, possess no money, and had existed for thousands of generations. Unlike Philo, who did not mention any particular geographical location of the Essenes other than the whole land of Israel, Pliny places them in Ein Gedi, next to the Dead Sea.

A little later Josephus gave a detailed account of the Essenes in The Jewish War (c. 75 CE), with a shorter description in Antiquities of the Jews (c. 94 CE) and The Life of Flavius Josephus (c. 97 CE). Claiming first hand knowledge, he lists the Essenoi as one of the three sects of Jewish philosophy[7] alongside the Pharisees and the Sadducees. He relates the same information concerning piety, celibacy, the absence of personal property and of money, the belief in communality and commitment to a strict observance of Sabbath. He further adds that the Essenes ritually immersed in water every morning, ate together after prayer, devoted themselves to charity and benevolence, forbade the expression of anger, studied the books of the elders, preserved secrets, and were very mindful of the names of the angels kept in their sacred writings.

 

CATHOLIC ENCYCLOPEDIA: Essenes - New Advent

www.newadvent.org › Catholic Encyclopedia › E‎

One of three leading Jewish sects mentioned by Josephus as flourishing in the second century B.C., the others being the Pharisees and the Sadducees.

 

ESSENES

 

T
=
2
-
7
THE
33
15
6
-
-
-
-
-
-
-
-
-
E
=
5
-
-
ENNEAD
-
-
-
-
-
-
-
1
E
5
5
5
-
-
-
-
1
N
14
5
5
-
-
-
-
1
N
14
5
5
-
-
-
-
1
E
5
5
5
-
-
-
-
2
A+D
5
5
5
E
=
5
-
6
ENNEAD
43
25
25
-
-
-
-
-
-
4+3
2+5
2+5
E
=
5
-
6
ENNEAD
7
7
7
-
-
-
-
-
-
1+4
-
-
E
=
5
-
6
ENNEAD
7
7
7

 

 

T
=
2
-
7
THE
33
15
6
-
-
-
-
-
-
-
-
-
E
=
5
-
-
ENNEA
-
-
-
-
-
-
-
1
E
5
5
5
-
-
-
-
1
N
14
5
5
-
-
-
-
1
N
14
5
5
-
-
-
-
1
E
5
5
5
-
-
-
-
2
A
1
1
1
E
=
5
-
6
ENNEA
39
21
21
-
-
-
-
-
-
3+9
2+1
2+1
E
=
5
-
6
ENNEA
12
3
3
-
-
-
-
-
-
1+2
-
-
E
=
5
-
6
ENNEA
3
3
3

 

 

T
=
2
-
3
THE
33
15
6
E
=
5
-
5
ENNEA
39
21
3
-
-
7
-
8
Add to Reduce
72
36
9
-
-
-
-
-
Reduce to Deduce
7+2
3+6
-
-
-
7
-
8
Essence of Number
9
9
9

 

 

-
-
-
-
-
THE
-
-
-
T
=
2
-
1
T
20
2
2
H
=
8
-
1
H
8
8
8
E
=
5
-
1
E
5
5
5
-
-
15
-
3
THE
33
15
15
-
-
-
-
-
FAMILY
-
-
-
F
=
6
-
1
F
6
6
6
A
=
1
-
1
A
1
1
1
M
=
4
-
1
M
13
4
4
I
=
9
-
1
I
9
9
9
L
=
3
-
1
L
12
3
3
Y
=
7
-
1
Y
25
7
7
-
-
30
-
6
FAMILY
66
30
30
-
-
-
-
-
-
-
-
-
-
-
45
-
9
First Total
99
45
45
-
-
4+5
-
-
Add to Reduce
9+9
4+5
4+5
-
-
9
-
9
Second Total
18
9
9
-
-
-
-
-
Reduce to Deduce
1+8
-
-
-
-
9
-
9
Essence of Number
9
9
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
THE
-
-
-
-
-
-
-
-
-
-
-
-
-
T
=
2
-
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
H
=
8
-
1
H
8
8
8
-
-
-
-
-
-
-
-
8
-
E
=
5
-
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
-
-
15
-
3
THE
33
15
15
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
FAMILY
-
-
-
-
-
-
-
-
-
-
-
-
-
F
=
6
-
1
F
6
6
6
-
-
-
-
-
-
6
-
-
-
A
=
1
-
1
A
1
1
1
-
1
-
-
-
-
-
-
-
-
M
=
4
-
1
M
13
4
4
-
-
-
-
4
-
-
-
-
-
I
=
9
-
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
L
=
3
-
1
L
12
3
3
-
-
-
3
-
-
-
-
-
-
Y
=
7
-
1
Y
25
7
7
-
-
-
-
-
-
-
7
-
-
-
-
30
-
6
FAMILY
66
30
30
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
45
-
9
First Total
99
45
45
-
1
2
3
4
5
6
7
8
9
-
-
4+5
-
-
Add to Reduce
9+9
4+5
4+5
-
-
-
-
-
-
-
-
-
-
-
-
9
-
9
Second Total
18
9
9
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
Reduce to Deduce
1+8
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
-
9
Essence of Number
9
9
9
-
1
2
3
4
5
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
THE
-
-
-
-
-
-
-
-
-
-
-
-
-
T
=
2
-
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
H
=
8
-
1
H
8
8
8
-
-
-
-
-
-
-
-
8
-
E
=
5
-
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
F
=
6
-
1
F
6
6
6
-
-
-
-
-
-
6
-
-
-
A
=
1
-
1
A
1
1
1
-
1
-
-
-
-
-
-
-
-
M
=
4
-
1
M
13
4
4
-
-
-
-
4
-
-
-
-
-
I
=
9
-
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
L
=
3
-
1
L
12
3
3
-
-
-
3
-
-
-
-
-
-
Y
=
7
-
1
Y
25
7
7
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
FAMILY
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
45
-
9
First Total
99
45
45
-
1
2
3
4
5
6
7
8
9
-
-
4+5
-
-
Add to Reduce
9+9
4+5
4+5
-
-
-
-
-
-
-
-
-
-
-
-
9
-
9
Second Total
18
9
9
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
Reduce to Deduce
1+8
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
-
9
Essence of Number
9
9
9
-
1
2
3
4
5
6
7
8
9

 

 

-
-
-
-
-
-
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
THE
-
-
-
-
-
-
-
-
-
-
-
-
-
A
=
1
-
1
A
1
1
1
-
1
-
-
-
-
-
-
-
-
T
=
2
-
1
T
20
2
2
-
-
2
-
-
-
-
-
-
-
L
=
3
-
1
L
12
3
3
-
-
-
3
-
-
-
-
-
-
M
=
4
-
1
M
13
4
4
-
-
-
-
4
-
-
-
-
-
E
=
5
-
1
E
5
5
5
-
-
-
-
-
5
-
-
-
-
F
=
6
-
1
F
6
6
6
-
-
-
-
-
-
6
-
-
-
Y
=
7
-
1
Y
25
7
7
-
-
-
-
-
-
-
7
-
-
H
=
8
-
1
H
8
8
8
-
-
-
-
-
-
-
-
8
-
I
=
9
-
1
I
9
9
9
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
FAMILY
-
-
-
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
45
-
9
First Total
99
45
45
-
1
2
3
4
5
6
7
8
9
-
-
4+5
-
-
Add to Reduce
9+9
4+5
4+5
-
-
-
-
-
-
-
-
-
-
-
-
9
-
9
Second Total
18
9
9
-
1
2
3
4
5
6
7
8
9
-
-
-
-
-
Reduce to Deduce
1+8
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
-
9
Essence of Number
9
9
9
-
1
2
3
4
5
6
7
8
9

 

 

T
=
2
-
3
THE
33
15
6
F
=
6
-
6
FAMILY
66
30
3
-
-
8
-
9
First Total
99
45
9
-
-
-
-
-
Add to Reduce
9+9
4+5
-
-
-
8
-
9
Second Total
18
9
9
-
-
-
-
-
Reduce to Deduce
1+8
-
-
-
-
8
-
9
Essence of Number
9
9
9

 

 

-
10
M
I
N
D
-
M
A
T
T
E
R
-
-
-
-
-
--
-
-
-
-
-
-
-
9
5
-
-
-
-
-
-
-
-
+
=
14
1+4
=
5
=
5
=
5
-
-
-
9
14
-
-
-
-
-
-
-
-
+
=
23
2+3
=
5
=
5
=
5
-
10
M
I
N
D
-
M
A
T
T
E
R
-
-
-
-
-
--
-
-
-
-
-
-
4
-
-
4
-
4
1
2
2
5
9
+
=
31
3+1
=
4
=
4
=
4
-
-
13
-
-
4
-
13
1
20
20
5
18
+
=
94
9+4
=
13
1+3
4
=
4
-
10
M
I
N
D
-
M
A
T
T
E
R
-
-
-
-
-
--
-
-
-
-
-
-
13
9
14
4
-
13
1
20
20
5
18
+
=
117
1+1+7
=
9
=
9
=
9
-
-
4
9
5
4
-
4
1
2
2
5
9
+
=
45
4+5
=
9
=
9
=
9
-
10
M
I
N
D
-
M
A
T
T
E
R
-
-
-
-
-
-
-
-
-
-
-
-`
-
-
-
-
-
-
1
-
-
-
-
-
-
1
occurs
x
1
=
1
=
1
-
-
-
-
-
-
-
-
-
2
2
-
-
-
-
2
occurs
x
2
=
4
=
4
3
-
-
--
--
--
--
--
--
--
--
--
--
--
--
3
--
--
--
--
--
--
--
-
-`
4
-
-
4
-
4
-
-
-
-
-
-
-
4
occurs
x
3
=
12
1+2
3
-
-
-
-
5
-
-
-
-
-
-
5
-
-
-
5
occurs
x
2
=
10
1+0
1
6
-
-
--
--
--
--
--
--
--
--
--
--
--
--
6
--
--
--
--
--
--
--
7
-
-
--
--
--
--
--
--
--
--
--
--
--
--
7
--
--
--
--
--
--
--
8
-
-
--
--
--
--
--
--
--
--
--
--
--
--
8
--
--
--
--
--
--
--
-
-
-
9
-
-
-
-
-
-
-
-
9
-
-
9
occurs
x
2
=
18
1+8
9
24
10
M
I
N
D
-
M
A
T
T
E
R
-
-
21
-
-
10
-
45
-
18
2+4
-
-
9
-
-
-
-
-
-
-
-
9
-
-
2+1
-
-
1+0
-
4+5
-
1+8
6
10
M
I
N
D
-
M
A
T
T
E
R
-
-
3
-
-
1
-
9
-
9

 

 

4
MIND
40
22
4
5
LIGHT
56
29
2
4
DARK
34
16
7
6
MATTER
77
23
5
19
Add to Reduce
207
90
18
10
Reduce to Deduce
2+0+7
9+0
1+8
1
Essence of Number
9
9
9

 

 

4
EVER
50
23
5
7
FOREVER
89
44
8

 

 

3
THE
33
15
6
7
ETERNAL
75
30
3
10
Add to Reduce
108
45
9
1+0
Reduce to Deduce
1+0+8
4+5
-
1
Essence of Number
9
9
9

 

 

8
AMOR FATI
-
-
-
1
AMOR
47
20
2
-
FATI
36
18
9
8
AMOR FATI
83
38
11
-
8+3
3+8
1+1
8
AMOR FATI
11
11
2
-
1+1
1+1
-
8
AMOR FATI
2
2
2

 

 

5
LIGHT
56
29
2
5
SIGHT
63
18
9
4
EYES
54
18
9

 

 

8
ECCE HOMO
67
40
4

 

 

12
BEHOLD THE MAN
-
-
-
1
BEHOLD
46
28
1
-
THE
33
15
6
1
MAN
28
10
1
12
BEHOLD THE MAN
107
53
8
1+2  
1+0+7
5+3
-
3
BEHOLD THE MAN
8
8
8

 

 

-
-
-
-
THE MAGICAL ALPHABET
-
-
-
T
=
2
3
THE
33
15
6
M
=
4
7
MAGICAL
46
28
1
A
=
1
8
ALPHABET
65
29
2
-
-
7
18
THE MAGICAL ALPHABET
144
72
9
-
-
-
1+8
-
1+4+4
7+2
-
-
-
7
9
THE MAGICAL ALPHABET
9
9
9

 

 

-
18
T
H
E
-
M
A
G
I
C
A
L
-
A
L
P
H
A
B
E
T
-
-
-
-
--
-
-
-
-
-
-
-
-
8
-
-
-
-
-
9
-
-
-
-
-
-
-
8
-
-
-
-
+
=
25
2+5
=
7
=
7
=
7
-
-
-
8
-
-
-
-
-
9
-
-
-
-
-
-
-
8
-
-
-
-
+
=
25
2+5
=
7
=
7
=
7
-
18
T
H
E
-
M
A
G
I
C
A
L
-
A
L
P
H
A
B
E
T
-
-
-
-
-
-
-
-
-
-
-
-
2
-
5
-
4
1
7
-
3
1
3
-
1
3
7
-
1
2
5
2
+
=
47
4+7
=
11
1+1
2
=
2
-
-
20
-
5
-
13
1
7
-
3
1
12
-
1
12
16
-
1
2
5
20
+
=
119
1+1+9
=
11
1+1
2
=
2
-
18
T
H
E
-
M
A
G
I
C
A
L
-
A
L
P
H
A
B
E
T
-
-
-
-
-
-
-
-
-
-
-
-
20
8
5
-
13
1
7
9
3
1
12
-
1
12
16
8
1
2
5
20
+
=
144
1+4+4
=
9
=
9
=
9
-
-
2
8
5
-
4
1
7
9
3
1
3
-
1
3
7
8
1
2
5
2
+
=
72
7+2
=
9
=
9
=
9
-
18
T
H
E
-
M
A
G
I
C
A
L
-
A
L
P
H
A
B
E
T
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
1
-
-
1
-
-
-
1
-
-
-
-
-
1
occurs
x
4
=
4
=
4
-
-
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
2
-
2
-
-
2
occurs
x
3
=
6
=
6
-
-
-
-
-
-
-
-
-
-
3
-
3
-
-
3
-
-
-
-
-
-
-
-
3
occurs
x
3
=
9
=
9
-
-
-
-
-
-
4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
4
occurs
x
1
=
4
=
4
-
-
-
-
5
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
5
-
-
-
5
occurs
x
2
=
10
1+0
1
6
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
6
SIX
6
-
-
-
-
-
-
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
7
occurs
x
2
=
14
1+4
5
-
-
-
8
-
-
-
-
-
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
8
occurs
x
2
=
16
1+6
7
-
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
occurs
x
1
=
9
=
9
6
18
T
H
E
-
M
A
G
I
C
A
L
-
A
L
P
H
A
B
E
T
-
-
39
-
-
18
-
72
-
45
-
1+8
-
-
-
-
--
1
-
-
-
1
-
-
1
-
-
-
1
-
-
-
-
-
3+9
-
-
1+8
-
7+2
-
4+5
6
9
T
H
E
-
M
A
G
I
C
A
L
-
A
L
P
H
A
B
E
T
-
-
12
-
-
9
-
9
-
9
-
-
2
8
5
-
4
1
7
9
3
1
3
-
1
3
7
8
1
2
5
2
-
-
1+2
-
-
--
-
-
-
-
6
9
T
H
E
-
M
A
G
I
C
A
L
-
A
L
P
H
A
B
E
T
-
-
3
-
-
9
-
9
-
9

 

 

18
T
H
E
-
M
A
G
I
C
A
L
-
A
L
P
H
A
B
E
T
-
-
-
-
--
-
-
-
-
-
-
-
8
-
-
-
-
-
9
-
-
-
-
-
-
-
8
-
-
-
-
+
=
25
2+5
=
7
=
7
=
7
-
-
8
-
-
-
-
-
9
-
-
-
-
-
-
-
8
-
-
-
-
+
=
25
2+5
=
7
=
7
=
7
18
T
H
E
-
M
A
G
I
C
A
L
-
A
L
P
H
A
B
E
T
-
-
-
-
-
-
-
-
-
-
-
2
-
5
-
4
1
7
-
3
1
3
-
1
3
7
-
1
2
5
2
+
=
47
4+7
=
11
1+1
2
=
2
-
20
-
5
-
13
1
7
-
3
1
12
-
1
12
16
-
1
2
5
20
+
=
119
1+1+9
=
11
1+1
2
=
2
18
T
H
E
-
M
A
G
I
C
A
L
-
A
L
P
H
A
B
E
T
-
-
-
-
-
-
-
-
-
-
-
20
8
5
-
13
1
7
9
3
1
12
-
1
12
16
8
1
2
5
20
+
=
144
1+4+4
=
9
=
9
=
9
-
2
8
5
-
4
1
7
9
3
1
3
-
1
3
7
8
1
2
5
2
+
=
72
7+2
=
9
=
9
=
9
18
T
H
E
-
M
A
G
I
C
A
L
-
A
L
P
H
A
B
E
T
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
1
-
-
1
-
-
-
1
-
-
-
-
-
1
occurs
x
4
=
4
=
4
-
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
2
-
2
-
-
2
occurs
x
3
=
6
=
6
-
-
-
-
-
-
-
-
-
3
-
3
-
-
3
-
-
-
-
-
-
-
-
3
occurs
x
3
=
9
=
9
-
-
-
-
-
4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
4
occurs
x
1
=
4
=
4
-
-
-
5
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
5
-
-
-
5
occurs
x
2
=
10
1+0
1
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
7
-
-
-
-
-
-
-
7
occurs
x
2
=
14
1+4
5
-
-
8
-
-
-
-
-
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
8
occurs
x
2
=
16
1+6
7
-
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
-
9
occurs
x
1
=
9
=
9
18
T
H
E
-
M
A
G
I
C
A
L
-
A
L
P
H
A
B
E
T
-
-
39
-
-
18
-
72
-
45
1+8
-
-
-
-
--
1
-
-
-
1
-
-
1
-
-
-
1
-
-
-
-
-
3+9
-
-
1+8
-
7+2
-
4+5
9
T
H
E
-
M
A
G
I
C
A
L
-
A
L
P
H
A
B
E
T
-
-
12
-
-
9
-
9
-
9
-
2
8
5
-
4
1
7
9
3
1
3
-
1
3
7
8
1
2
5
2
-
-
1+2
-
-
--
-
-
-
-
9
T
H
E
-
M
A
G
I
C
A
L
-
A
L
P
H
A
B
E
T
-
-
3
-
-
9
-
9
-
9

 

 

18
T
H
E
M
A
G
I
C
A
L
A
L
P
H
A
B
E
T
-
-
-
-
--
-
-
-
-
-
-
-
8
-
-
-
-
9
-
-
-
-
-
-
8
-
-
-
-
+
=
25
2+5
=
7
=
7
=
7
-
-
8
-
-
-
-
9
-
-
-
-
-
-
8
-
-
-
-
+
=
25
2+5
=
7
=
7
=
7
18
T
H
E
M
A
G
I
C
A
L
A
L
P
H
A
B
E
T
-
-
-
-
-
-
-
-
-
-
-
2
-
5
4
1
7
-
3
1
3
1
3
7
-
1
2
5
2
+
=
47
4+7
=
11
1+1
2
=
2
-
20
-
5
13
1
7
-
3
1
12
1
12
16
-
1
2
5
20
+
=
119
1+1+9
=
11
1+1
2
=
2
18
T
H
E
M
A
G
I
C
A
L
A
L
P
H
A
B
E
T
-
-
-
-
-
-
-
-
-
-
-
20
8
5
13
1
7
9
3
1
12
1
12
16
8
1
2
5
20
+
=
144
1+4+4
=
9
=
9
=
9
-
2
8
5
4
1
7
9
3
1
3
1
3
7
8
1
2
5
2
+
=
72
7+2
=
9
=
9
=
9
18
T
H
E
M
A
G
I
C
A
L
A
L
P
H
A
B
E
T
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
1
-
-
-
1
-
1
-
-
-
1
-
-
-
-
-
1
occurs
x
4
=
4
=
4
-
2
-
-
-
-
-
-
-
-
-
-
-
-
-
-
2
-
2
-
-
2
occurs
x
3
=
6
=
6
-
-
-
-
-
-
-
-
3
-
3
-
3
-
-
-
-
-
-
-
-
3
occurs
x
3
=
9
=
9
-
-
-
-
4
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
4
occurs
x
1
=
4
=
4
-
-
-
5
-
-
-
-
-
-
-
-
-
-
-
-
-
5
-
-
-
5
occurs
x
2
=
10
1+0
1
-
-
-
-
-
-
7
-
-
-
-
-
-
7
-
-
-
-
-
-
-
7
occurs
x
2
=
14
1+4
5
-
-
8
-
-
-
-
-
-
-
-
-
-
-
8
-
-
-
-
-
-
8
occurs
x
2
=
16
1+6
7
-
-
-
-
-
-
-
9
-
-
-
-
-
-
-
-
-
-
-
-
-
9
occurs
x
1
=
9
=
9
18
T
H
E
M
A
G
I
C
A
L
A
L
P
H
A
B
E
T
-
-
39
-
-
18
-
72
-
45
1+8
-
-
-
--
1
-
-
-
1
-
1
-
-
-
1
-
-
-
-
-
3+9
-
-
1+8
-
7+2
-
4+5
9
T
H
E
M
A
G
I
C
A
L
A
L
P
H
A
B
E
T
-
-
12
-
-
9
-
9
-
9
-
2
8
5
4
1
7
9
3
1
3
1
3
7
8
1
2
5
2
-
-
1+2
-
-
--
-
-
-
-
9
T
H
E
M
A
G
I
C
A
L
A
L
P
H
A
B
E
T
-
-
3
-
-
9
-
9
-
9

 

 

ABCDEFGHIJKLMNOPQRSTUVWXYZZYXWVUTSRQPONMLKJIHGFEDCBA

12345678910111213141516171819202122232425262625242322212019181716151413121110987654321

ABCDEFGHIJKLMNOPQRSTUVWXYZZYXWVUTSRQPONMLKJIHGFEDCBA

 

 

G
=
7
-
3
GOD
26
17
8
I
=
9
-
2
IS
28
10
1
Z
=
8
-
4
ZERO
64
28
1
O
=
6
-
3
ONE
34
16
7
I
=
9
-
2
IS
28
10
1
-
-
39
-
14
First Total
180
81
18
-
-
3+9
-
1+4
Add to Reduce
1+8+0
8+1
1+8
-
-
12
-
5
Second Total
9
9
9
-
-
1+2
-
-
Reduce to Deduce
-
-
-
-
-
3
-
5
Essence of Number
9
9
9

 

 
 
Top
  
 
Evokation
  
Previous Page
Index
 Next Page